思维图形化方法的应用＊——谈高三复习课中“几何光学”的教学设计

马国伟

（常州市第二中学，江苏 常州 213003）

1 教材分析及教学策略

几何光学是以光的直线传播为基础，采用几何方法研究光在透明介质中的传播问题.本课知识点主要包含光的反射，折射和全反射现象，知识难度不大.但近几年高考中几何光学出现频率很高，是高考的一大热点.在复习中我们采用以思维图形化方法为主线，知识为载体的方式突破相关问题的重点和难点.

2 教学目标

（1）知识与技能.

① 理解折射定律和折射率的概念；

② 理解并掌握光的全反射现象和发生全反射的条件.

（2）过程与方法.

掌握思维图形化方法在解决几何光学问题中的应用.

（3）情感态度、价值观.

① 理解思维图形化对解决物理问题的重要性；

② 感受在学习工作中应用思维图形化带来的便利.

3 教学重点与难点

（1）教学重点：思维图形化的应用.

（2）教学难点：全反射的临界问题分析.

4 课前准备

笔记本电脑（连接网络，打开QQ），投影仪，手机（打开QQ）.

5 新课引入

在解决物理问题时，为了防止问题过于抽象导致问题的无法解决，我们往往采用将物理问题通过图形的方式分析以降低问题的难度，达到解决问题的目的.这种方法我们可以称为思维图形化.

今天我们复习新的内容——几何光学，就需要思维图形化的方法.下面请几位同学将学案中的基础梳理填空答案核对一下.（学生回答填空答案，在学生有错误时老师予以更正）

6 进入新课

____师：（投影）下面请看投影，这2幅图是光线由空气进入玻璃和由玻璃进入空气的反射和折射如图1所示.观察2幅图发现在图中除了有入射光线，反射光线，折射光线外还有什么呢？

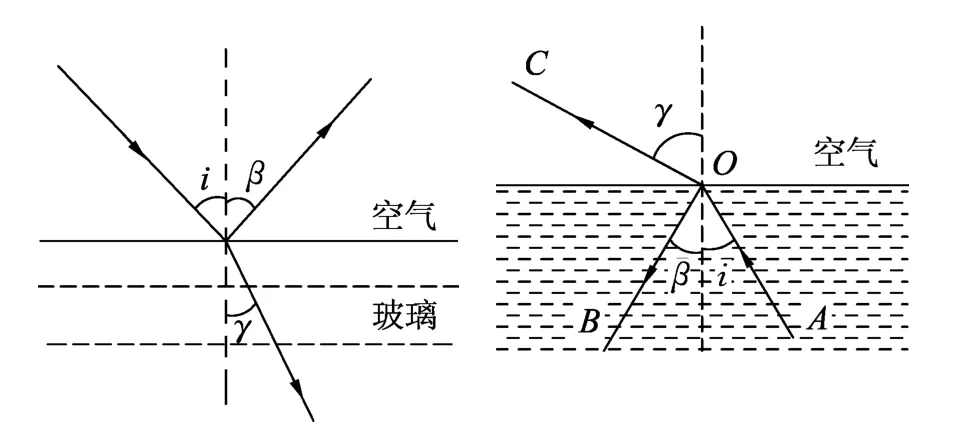
图1

生：还有分界面和法线，入射角，反射角和折射角.

师：法线具有什么特点？

生：法线与分界面垂直.

师：经过研究发现，光的反射，折射全反射有以下规律.（教师投影）

（1）反射角等于入射角i＝β；

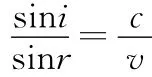
师：我们如何利用这些知识解决几何光学问题呢？请看例1.（学生思考题目，教师观察学生做题情况，将学生出现的典型解题错误用手机QQ拍照发送到笔记本电脑QQ上）

（1）两条光线射出玻璃后的交点与O点的距离；

（2）光线Ⅱ从A点入射到与光线I相交所用的时间.

（教师投影展示学生错误分析的图片）

分析学生情况，学生几乎没有作图，问题根本无法解决.如图3、4，学生作图，但所作图形是错误的，问题还是不能解决.

图2

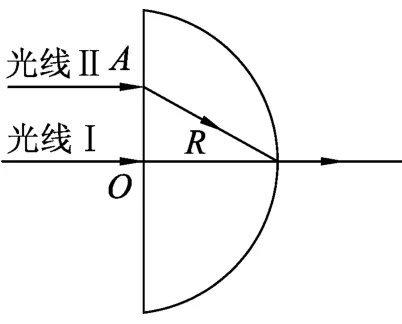
图3

图4

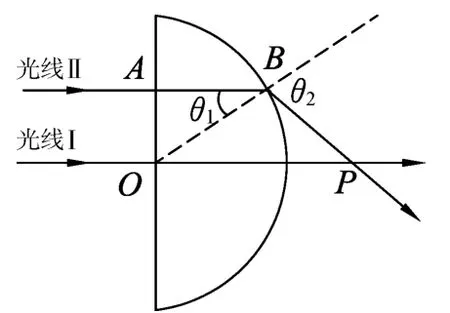
图5

（教师总结并投影）要解决几何光学问题我们需要3步：（1）根据题意作出光路图；（2）利用光路图寻找几何关系；（3）根据对问题的分析写表达式并根据必要的推理写表达式求解.

师：根据由例1总结的思维图形化解决几何光学的步骤，请同学们求解例2.（学生思考并解决问题，教师观察学生做题情况，将学生出现的典型解题错误用手机QQ拍照发送到笔记本电脑QQ上）

例2.（2013年江苏省高考卷）图6为单反照相机取景器的示意图，ABCDE为五棱镜的一个截面，AB⊥BC.光线垂直AB射入，分别在CD和EA上发生反射，且两次反射的入射角相等，最后光线垂直BC射出.若两次反射都为全反射，则该五棱镜折射率的最小值是多少？（计算结果可用三角函数表示）

（教师投影展示学生错误分析图片）

图7错误审题不清，没有注意题目两次反射.图8的错误也是审题不清，没有关注到全反射.而图9的错误为没有关注出射光线垂直于BC，导致作图错误.

图6

图7

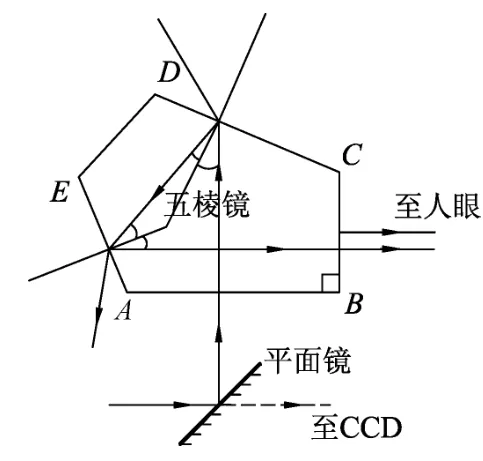
图8

图9

图10

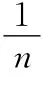
师：前面2个问题都是只有1条入射光线，我们直接作出光路图即可，那么如果出现一组光线会怎样呢？请看例3.（学生思考并解决问题，教师观察学生的做题情况，将学生的典型错误用手机QQ拍照发送到笔记本电脑QQ上）

例3.（2010年重庆高考卷）如图11所示，空气中有一折射率为的玻璃柱体，其横截面是圆心角为90°，半径为R的扇形OAB.一束平行光平行于横截面，以45°入射角照射到OA上，OB不透光.若只考虑首次入射到圆弧AB上的光，则圆弧AB上有光透出部分的弧长为

图11

（教师投影展示学生错误分析图片）如图12，学生很容易得到过O点的光线折射情况，但会错误认为所有光线都从圆弧出射.

教师给予正确分析：如图13，从中可以发现，随着入射光线向左平移，在圆弧AB上光线的入射角逐渐增大，当入射角增大到45°时，发生全反射，假设此时为Q点.则有∠AOQ＝15°，又因∠BOP＝30°，可见出射光线部分为圆弧PQ.所以选（B）选项.

图12

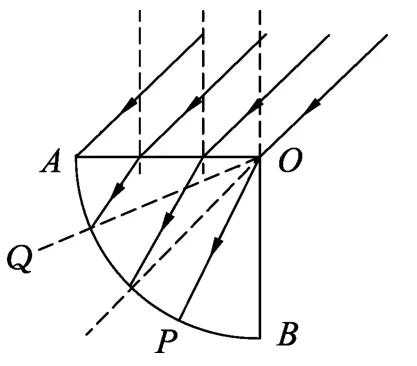
图13

教师总结：如果问题出现有一组光线，我们可以通过寻找共同情况和变化情况，使思维图形化完善而予以解决.

师：如果根本就没有给任何入射光线的问题该怎么办呢？请看例4.

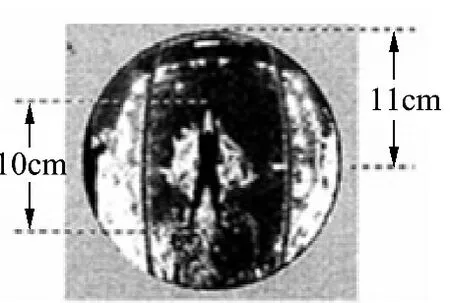
图14

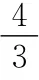
问题分析：本题在利用思维图形化时需要突破2个问题：（1）转换观察视角；（2）寻找光线临界点.而要得到结果还要突破第3个问题：参照实际情况估算.需要教师引导学生一步一步突破.

第1步突破——转换观察视角.

师：我们所看到的照片是怎么拍摄出来的呢？

生：光线进入照相机镜头在底片上成像.

师：那么这些光线与照片在一个平面内吗？

生：不在.

师：为了能够分析光路图，我们该怎么办呢？

生：转换观察视角.

第2步突破——寻找临界点.

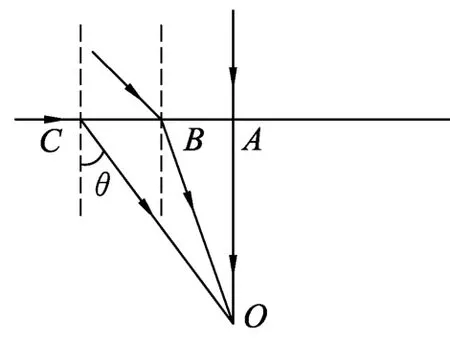
图15

如图15，O点为照相机所在位置，直线ABC为水面，过O点正上方的A点的光线可以垂直入射进入照相机.过与A点相距不远的B点的光线也有一条折射后进入O点.那么是不是所有位置都可以有光线折射后到达O点呢？不是.当折射角θ等于临界角时，入射角为90°，再向外的所有点的光线都不能经折射到达O点.

第3步突破——参照实际情况估算.

运动员手到脚的实际长度大约为2.1m，按照比例关系，可求得实际半径.

教师总结：在利用思维图形化解题时，为了能够做出思维图形，有时需要转换观察视角，寻求临界条件.

总之，思维图形化是高中物理在解决问题时分析问题的一种常用方法.除在几何光学中做出光路图外，在力学问题中有受力分析图，运动问题中有运动简图和速度－时间图像，电路问题中有等效电路图，电磁场问题中为形象描述引入了电场线和磁感线，这些都是思维图形化方法的应用.这种方法可以有效地降低问题的思维难度，有利于问题的解决，但作图时务必要规范、准确、全面.

1 杨万林.暴露思维过程 重视图形演变 培养创新意识［J］.科学大众·教师版，2012（3）.

2 孙路弘.让图形展示思维的精彩［J］.销售与市场·营销版，2007（2）.

3 刘霁华.以方法为主线的物理教学［J］.物理教学，2008（8）.