“瞬时过程”问题的特点与应用
徐君生
(江苏省扬中高级中学,江苏扬中 212200)
物理综合试题通常都会有较复杂的物理过程,如果把物理综合试题类比于一头“牛”的话,则过程分析就相当于“庖丁解牛”,即通过过程分析把一个复杂的物理过程(相当于一头完整的牛)分解为若干个较为简单的、单一的物理过程,在此基础上再各个击破,从而顺利解决物理综合试题.由此可见过程分析对解决物理问题至关重要.而过程分析的基础是各个单一的物理过程有何特点以及该特点如何应用等,所以单一的物理过程的特点与特点的应用是解决物理综合试题的重中之重.而在众多的物理过程中,瞬时过程又较为特殊:一是瞬时过程通常包含着隐含条件,不同的瞬时过程包含的隐含条件一般不同;二是因其时间较短(相当于实际生活中俗话所说的“不起眼”)而极容易在过程分析中被忽视.有鉴于此,本文试就对中学物理中所涉及到的瞬时过程做一归纳小结,以期能对物理的教与物理的学起到丁点作用.
1 与轻绳有关的瞬时过程特点与应用
轻绳的基本特点可概括为3点:一是“轻”,因为细绳很细很轻,所以可忽略细绳的质量;二是“软”,认为轻绳只能产生拉力不能产生支持力,且拉力方向一定沿轻绳方向;三是“不可伸长”,认为轻绳产生的弹力是因为轻绳发生微小形变而产生,该形变极小,可忽略不计.
1.1 绳瞬时绷紧问题
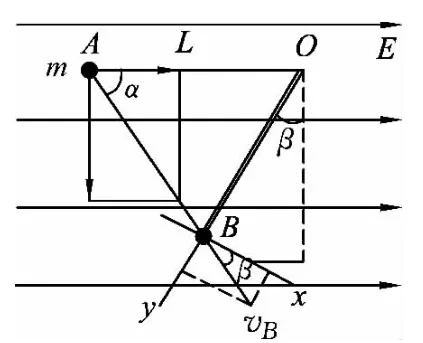
图1
绳瞬时绷紧的特点是从轻绳基本特点之三演变而来.因轻绳不可伸长,故在绳绷紧后不可能有沿绳方向的使绳拉长的速度,即在短时间内使沿绳方向的分速度减为零,所以在绳绷紧的瞬间存在机械能的损失,因此一定要切记决不能因该过程的时间极短就可忽略,尤其是在应用动能定理时决不能应用所谓的“全程法”.处理该过程的基本方法是正交分解法,即把绷紧前物体的瞬时速度沿绳方向与垂直于绳方向正交分解,在绷紧后的瞬间物体只保留垂直于绳方向上的分速度.
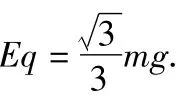

1.2 绳瞬时碰钉子问题
由轻绳的基本特点可知,由于轻绳的弹力只能沿绳方向,故物体只要没有沿绳方向发生位移,则绳的拉力就不做功,由动能定理可知,在该瞬时过程中物体的动能不发生变化,即在此瞬时过程中物体的速度不发生变化.
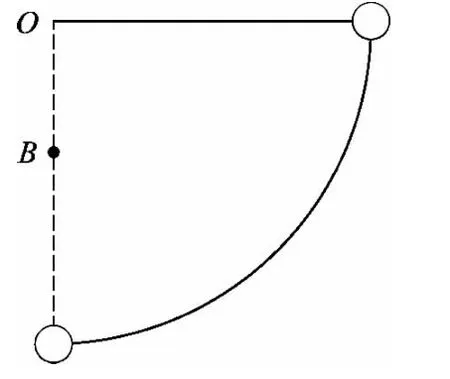
图2
例2.如图2所示,将悬线拉至水平位置无初速释放,到达最低点时,细线被一与悬点同一竖直线上的小钉B挡住,则比较悬线被小钉挡住前后瞬间,下列说法正确的是
(A)小球的角速度减小.
(B)小球动能减小.
(C)悬线的张力变大.
(D)小球的向心加速度变大.解析:细线碰到钉子的瞬间,由于绳拉力不做功,重力不做功,所以小球的动能(速度)不变.小球做圆周运动的半径变小,所以角速度、向心加速度及绳拉力均变大,正确选项为(C)、(D).
1.3 绳瞬时剪断时的加速度问题
因发生的是微小形变,其形变量极小,几乎可忽略不计,所以形变量的变化几乎不需要时间,故其产生的弹力大小的变化几乎不需要时间.因此因微小形变而产生的弹力可以突变,而发生明显形变产生的弹力如橡皮绳及弹簧之类的弹力,因形变量的变化需要一定的时间,故其产生的弹力大小不能突变.
例3.如图3所示,质量为m的小球用两根细绳OA、OB拴住处于静止状态.求:
(1)剪断细绳OA的瞬间,小球的加速度;
(2)剪断细绳OB的瞬间,小球的加速度.
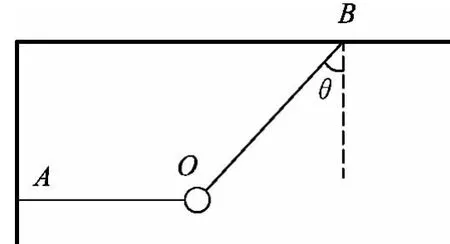
图3
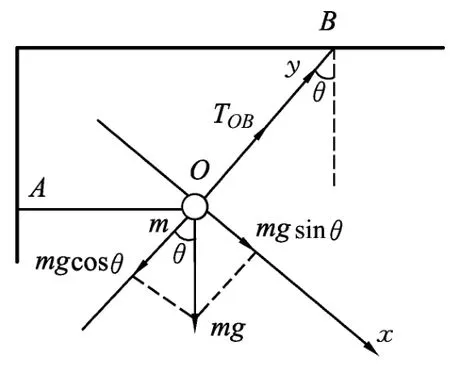
图4
(1)剪断OA的瞬间,小球绕B点做圆周运动,建立如图4所示的正交坐标轴并分解,分别列出x、y方向的牛顿第二定律方程,即y方向TOB=mgcosθ,x方 向mgsinθ=max,解得a1=gsinθ方向沿图中x方向.(2)若剪断细线OB的瞬间,小球将绕A点做圆周运动,由牛顿第二定律易得TOA=0,a2=g.
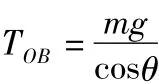
2 瞬时碰撞过程的特点与应用
两物体发生瞬时碰撞时,因撞击时间极短,由此得到碰撞具有4个特点(或者说是结论).
(1)因撞击的时间极短,撞击时产生的冲击力极大.如果把两个撞击的物体作为系统,则撞击时产生的冲击力为系统的内力,该系统在撞击瞬间都将满足(合外力为零时)或近似满足(合外力不为零,但内力远大于外力)动量守恒.
(2)因撞击时间极短,故在此过程中近似认为两物体尚未发生位移(即在短时间内物体的速度发生了变化,但其位置没有变化).
(3)间接参与的物体在此瞬时过程中其运动状态几乎不变.所谓间接参与的物体就相当于是一辆汽车里的乘客,当两辆汽车发生碰撞时,乘客并没有直接参与碰撞,而是间接参与者.
(4)碰撞时间虽短,但一般存在机械能损失.
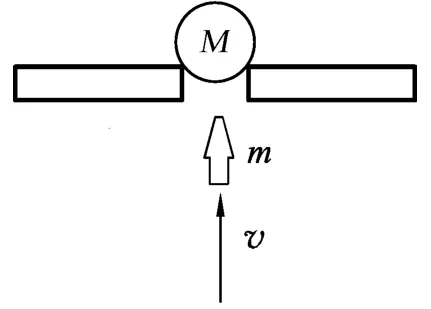
图5
例4.如图5所示,质量为m的子弹以速度v从正下方向上击穿一个静止在水平面上、质量为M的木球,击穿后木球上升的高度为H,求击穿后子弹能上升的高度.
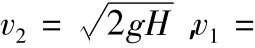
动量守恒与能量守恒相结合一般有两种形式,一是以子弹打木块为典型形式,两物体之间通过摩擦力发生相互联系;另一种就是以弧形槽为典型形式.
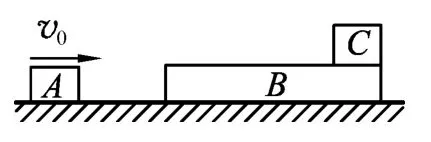
图6
例5.如图6所示,木板A质量mA=2 kg,足够长的木板B质量mB=4 kg,质量为mC=5 kg的木块C静置于木板B上,水平面光滑,B、C之间有摩擦,动摩擦因素μ=0.4.现使A以v0=10 m/s的初速度向右运动,与B碰撞后粘合在一起.求:
(1)B运动过程中的最大速度大小;
(2)C运动过程中的最大速度大小;
(3)C相对于B滑行的位移(或改成:要使C物体不从B上表面滑离,B物体的长度至少要有多长).
解析:本题涉及到两个过程,先是A与B之间的瞬时碰撞,由碰撞特点1可知A与B组成的系统近似满足动量守恒(此时B物体受到C对其摩擦力作用,A与B组成的系统合外力不为0),由碰撞特点3可知,此过程中C物体属于间接参与者,故其运动状态几乎不变(原来C物体处于静止,碰撞后的瞬间C物体仍然处于静止).然后是B与C之间发生相对滑动,直到两者具有相同速度.
(1)根据以上分析不难知道A与B碰后瞬间,B速度最大.由A、B组成的系统动量守恒(取向右为正方向)有mAv0=(mA+mB)v1,代入数据得v1=4 m/s.
(2)B与C共速后,C速度最大,由A、B、C组成的系统动量守恒有mAv0=(mA+mB)v1=(mA+mB+mC)v2,代入数据得v2=2 m/s.
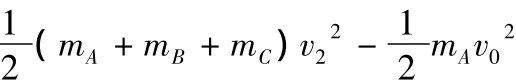
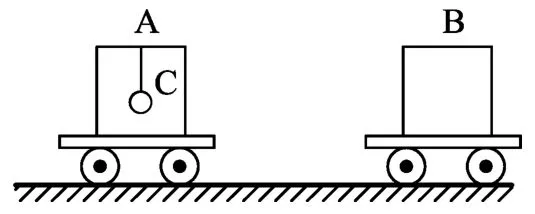
图7
例6.质量均为m,完全相同的两辆实验小车A和B停放在光滑水平面上,A车上另悬挂有质量为2m的小球C.开始B静止,A、C以速度v0向右运动,两车发生完全非弹性碰撞但不粘连,碰撞时间极短,碰后小球C先向右摆起,再向左摆起,每次绳均未达到水平(小车足够宽).如图7所示,求:
(1)小球第1次向右摆起至最大高度h1时小车A的速度大小vA.
(2)小球第1次向右摆起的最大高度h1和第1次向左摆起的最大高度h2之比.
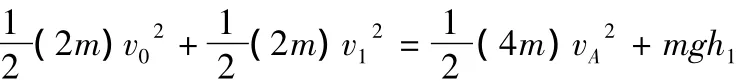
3 气体瞬时膨胀(或压缩)过程的特点与应用
气体瞬时膨胀(或压缩)过程的特点是,因时间极短,气体来不及与外界发生热交换,故该过程相当于是一个绝热过程.
例7.在轮胎爆裂这一短暂过程中
(A)气体急剧膨胀对外做功,温度升高.(B)气体做等温膨胀.
(C)气体膨胀,温度下降.
(D)气体等压膨胀,内能增加.
解析:轮胎爆裂时间极短,气体来不及与外界发生热交换,故Q≈0,因气体体积变大,对外做功,故W为负,由热力学第二定律可知ΔU为负,因一定质量的理想气体的内能只与温度有关,所以温度降低,正确选项为(C).
4 汽车恒定功率启动的瞬时加速度分析
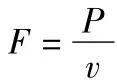
例8.一质量为m的汽车,设其牵引力是由其后轮的摩擦力提供,动摩擦因素为μ,汽车在平直公路上行驶时受到阻力大小为恒为f,汽车的额定功率为P,假设汽车以额定功率开始启动,试求:(1)汽车启动瞬间加速度多大?(2)经多长时间车轮与地面之间不再打滑?(3)汽车能达到的最大速度(假设f滑=μmg).
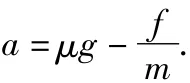
1 徐君生.与绳有关的物理模型[J].物理教学,2013(7):16-19.