完全弹性碰撞中的另一个不变量

刘 权

(苏州市陆慕高级中学，江苏苏州 215131)

1 提炼完全弹性碰撞中的不变量

1.1 建立小球碰撞模型

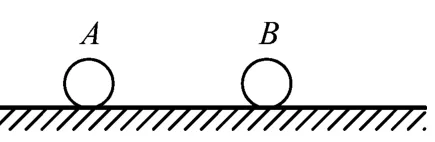
图1

如图1所示，在光滑的水平面上有A、B2个小球将发生完全弹性碰撞，A球的质量为m1，B球的质量为m2，设碰撞前A球的速度为v10，B球的速度为v20，碰撞后A球的速度为v1，B球的速度为v2，小球碰撞前后的速度方向未知.

1.2 提炼模型中的不变量

(1)碰撞过程中，系统动量不变.

表达式:m1v1+m2v2=m1v10+m2v20.

(2)碰撞过程中，系统能量不变.

由(1)、(2)式可求出

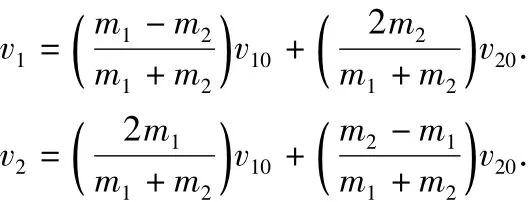
碰撞前小球A相对于B的速度为v10-v20.

碰撞后小球A相对于B的速度为v1-v2=v20-v10.

由动量和能量2个不变量又提炼出另一个不变量:碰撞过程中，小球相对速度大小不变.

2 例谈不变量在完全弹性碰撞中的优越性

动量定理和动能定理是在牛顿第二定律的基础上提炼出来的，因而动量定理和动能定理在运用过程中比牛顿第二定律有明显的优越性.同样，在完全弹性碰撞中提炼出来的不变量，在运用过程中一定有它的优越性.

例1.A、B2个小球在光滑的水平面上沿同一直线，同一方向运动，A球速度为5 m/s，B球速度为3 m/s，当A球追上B球时发生完全弹性碰撞，则碰撞后A，B2球速度的可能值

(A)3 m/s，5 m/s. (B)3 m/s，6 m/s.

(C)2 m/s，6 m/s. (D)-2 m/s，1 m/s.

解析:小球碰撞前相对速度大小为2m/s，由于在完全弹性碰撞过程中，小球相对速度大小不变，所以只有(A)选项正确.

点评:如果此题不利用相对速度这个不变量，操作起来很麻烦.由于2个小球质量未知，学生必须结合碰撞前后速度，动量守恒表达式和能量守恒表达式来计算小球质量，如果有解，说明正确，无解说明错误.而有部分学生给小球A、B质量赋值，分别为1 kg、2 kg，认为(A)选项错误的理由是:不满足动量守恒.殊不知在碰撞前后速度确定的情况下，两小球质量是确定的，但不是1 kg、2 kg.

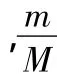
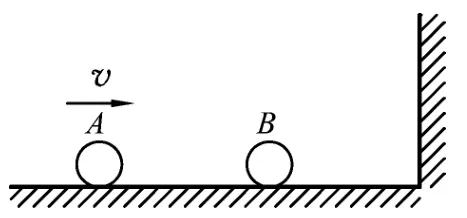
图2

解析:小球碰撞前相对速度大小为8 m/s，由于在完全弹性碰撞过程中，小球相对速度大小不变，设A球碰撞后速度大小为v1，那么B球碰撞后速度大小为8-v1.

根据系统动量守恒定律得8m=M(8-v1)+(-mv1).(规定向右为正方向)

点评:利用相对速度这个不变量以后，可以迅速得到v1≥4 m/s这个关系式，大大减小了计算量.

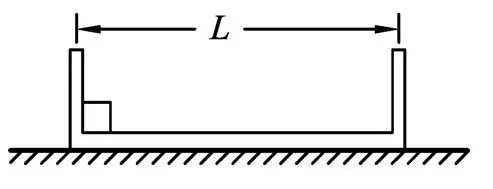
图3

例3.如图 3所示，一具有U型凹槽的扁长木板被置于水平光滑桌面上，凹槽内另放有一小木块，靠在左方槽边，设木块的质量为m，木板的质量为M，凹槽宽度L，木块与木板间的动摩擦因素为μ，木块的宽度远小于L.现快速用力拨动木块一下，使其在凹槽中滑动，由于木块的初速足够大，故得于在木板凹槽中来回碰撞木板槽边.设木块与木板槽边的碰撞皆为完全弹性碰撞，碰撞n次后恰好停止在凹槽的中央位置，求自木块被拨动至停止在木板中央时所经历的时间t.

解法1:研究木块被拨动至停止在木板中央的整个过程，设木块初速度为v，稳定时速度为v1.根据系统动量守恒定律得

根据动量定理得

根据系统能量守恒得

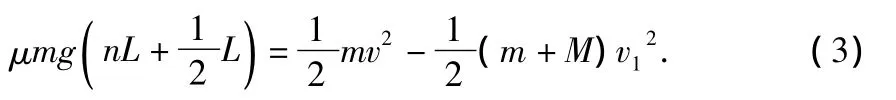
点评:解法1为常规方法，但思维量很大，涉及到3大定律，很多学生望而却步.解法2利用相对速度这个不变量，让木块相对于木板运动的过程变得连贯起来，最后以常见的思维方式处理了木块相对于木板的运动，式子简单精炼，减轻了学生的心理压力.当然学生要运用好解法2，必须深刻理解物体在完全弹性碰撞中的相对速度大小这个不变量.