基于GM(1，1)模型的郑州市商品房房价预测

闫鹏飞， 王 典， 燕慧慧

(1.郑州大学 水利与环境学院，河南 郑州450001;2.郑州大学 数学系，河南 郑州450001;3.郑州大学管理工程学院，河南郑州450001)

一、问题背景

在许多国家和地区房地产业已成为国民经济的支柱产业，是经济发展的重要力量。随着我国市场经济的发展，房地产在国民经济中的地位不断提高，影响不断扩大。上世纪90年代中后期，政府明确提出把房地产业作为国民经济新的增长点。房价的高低、升降不仅对经济的发展有很大的影响，同时也影响着人们的生活水平［1］。2012年7月，郑州市商品房房价达到每平方米6854元，再创历史新高。

对于房价的预测，目前的评论与分析大多侧重于政策、心理、资金、需求方面的定性分析，如张永胜从住房供给、货币政策、垄断开发商、土地政策、通货膨胀、地方财政收入等六个方面定性地分析了2009年房价持续上涨的原因，并通过对这些因素变化的分析，预计2010年中国房价将呈现一个温和爬升的趋势［2］;高成亮从供给和需求两方面详细地分析了影响房价的主要因素，定性地分析了信贷政策、价格预期、居民可支配收入、通货膨胀对房地产市场供求关系的影响，揭示了房价运行的规律［3］。

也有不少专家从定量的角度来分析影响房价走势和房地产行业发展的各类因素，建立了房价走势的预测模型［4-7］，如杨华对影响房价的一些主要因素建立房屋价格分析模型，进行归一化处理［8］。但更多的研究认为房价系统是一个灰色系统，通过建立GM(1，1)模型，得到房价的预测模型［1，9-10］。

灰色系统理论［11-16］于1982年由邓聚龙创立，20多年的飞速发展使灰色系统理论渗透到自然科学和社会科学的许多领域。灰色预测模型主要是利用GM(1，1)对时间序列进行预测，通过对数据进行处理，使其成为较有规律的时间序列数据。该模型只需要较少的样本数据就可作系统分析、模型建立、未来预测、行为决策和过程控制的特点，解决了以往由于数据少、信息不确定而无法研究或难以研究的问题，具有很强的预测性。因此，该模型在我国经济中得到非常广泛的应用。

通过查找文献，目前暂时没有得到基于灰色系统的对郑州市商品房房价作预测研究以及对其突变点作预测分析的文献。本文根据郑州市2010年1月—2012年7月商品房房价的实际数据(见表1)，建立GM(1，1)模型对郑州市商品房价格做出分析预测，并在此基础上建立灾变预测，预测郑州市商品房房价的突变点。

二、GM(1，1)模型的建立

(一)商品房房价预测的GM(1，1)模型的建立

房地产行业系统符合灰色系统特征。已知郑州市2010年1月—2012年7月的商品房房价，对郑州市商品房房价走势的时间序列建立灰色GM(1，1)预测模型。

表1 2010年1月—2012年7月郑州市商品房价格

设时间序列:x(0)=［x(0)(1)x(0)(2) … x(0)(n)］有n个观察值，通过累加生成新序列:x(1)=［x(1)(1)x(1)(2) … x(1)(n)］

其中:x(1)(k)=∑ki=1x(0)(i)，k=1，2，…，n

其中:α、μ为待估计参数，α称为发展灰数，μ称为内生控制系数。

解微分方程得时间响应函数:

相应的时间响应序列:

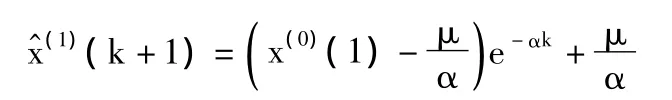
且［α μ］=(BTB)-1BTYn

则还原值(即预测值)为:

其中

可对此灰色模型进行matlab编程，求得参数α、μ，即可利用(0)(k+1)=^x(1)(k+1)-^x(1)(k)对未来郑州市商品房房价进行预测［9-21］。

(二)预测商品房房价的转折点——灾变预测模型的建立

假设商品房房价的突然上升与下降的点(即房价走势图上出现峰值的点)为灾变点(异常值)。设x为原始数列，xζ={x［q(1)］，x［q(2)］，…，x［q(m)］}⊂x 为灾变序列，则称Q(0)={q(1)，q(2)，…，q(m)}为灾变日期序列。其中，q(m)(≤n)为最近一次灾变发生的日期，对灾变日期序列进行灾变GM(1，1)建模。

三、计算结果

(一)房价预测GM(1，1)模型的计算结果

利用Matlab求得 α =-0.0068，μ=5421，则商品房的时间响应序列为 ^x(1)(k+1)=802067.88e0.0068k-797205.88，商品房房价的预测公式为^x(0)(k+1)=^x(1)(k+1)-^x(1)(k)=5472.65e0.0068k。

将郑州市2010年1月—2012年7月商品房房价、商品房房价的预测值以及预测值与实际房价的差值列表2。

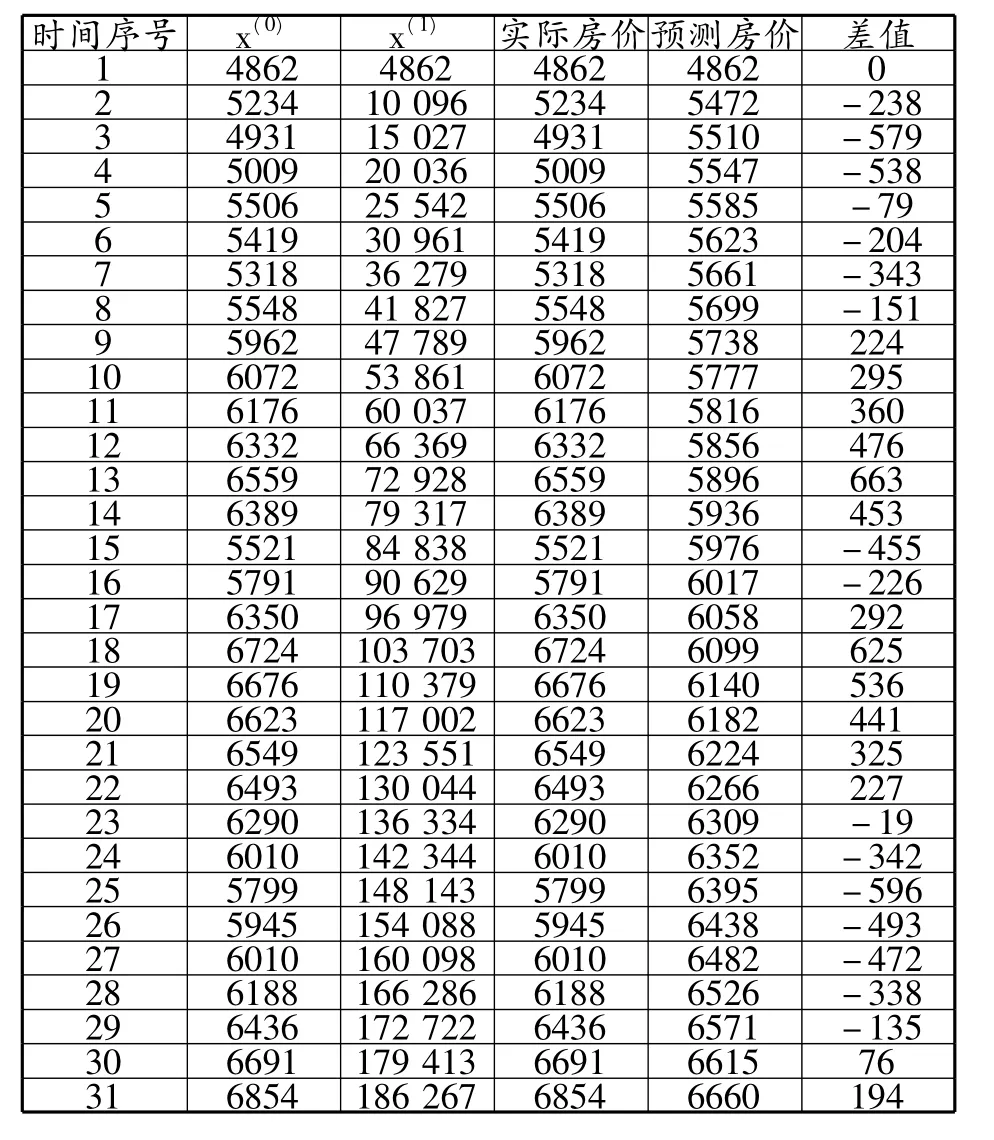
表2 房价预测的GM(1，1)模型的计算结果

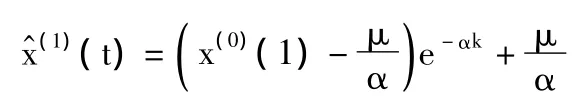
预测商品房房价走势如图1所示。

图1 预测商品房价走势

(二)预测商品房房价的转折点——灾变预测模型的建立

将表2中的实际商品房价按时间序列利用excel绘制散点图，如图2所示。

图2 实际商品房价走势

图2中，从直观上找出峰值点，则有:

做异常值x［q(i)］到出现灾变点q(i)的映射Q(0):x［q(i)］→q(i)，得灾变日期(转折点日期)序列Q(0)为Q(0)={q(1)，q(2)，q(3)，…，q(8)}={2，3，5，7，13，15，18，25}，据此对Q(0)建立灾变日期序列的GM(1，1)模型，利用Matlab求解得［α μ］=［-0.29 3.35］，即灾变日期(转折日期)序列的 GM(1，1)序列响应式为 ^q(1)(k+1)=13.55e0.29k-11.55，从而 ^q(k+1)=^q(1)(k+1)-^q(1)(k)=3.41e0.29k，Q(0)的模拟序列 ^Q(0)={^q(k)，k=2，3，4，…，8}={2，4.6，6.1，8.1，10.9，14.6，19.5，26.14}。计算下一次商品房房价的突变点:^q(8+1)≈35，^q(9)-^q(8)≈35-26=11，即从最近一次房价发生变动的时间算起，郑州商品房房价将在11个月之后有所回落，即在2012年12月份左右达到最高点，然后会有所回落。

四、计算结果后验差检验

后验差判别参照表见表3。

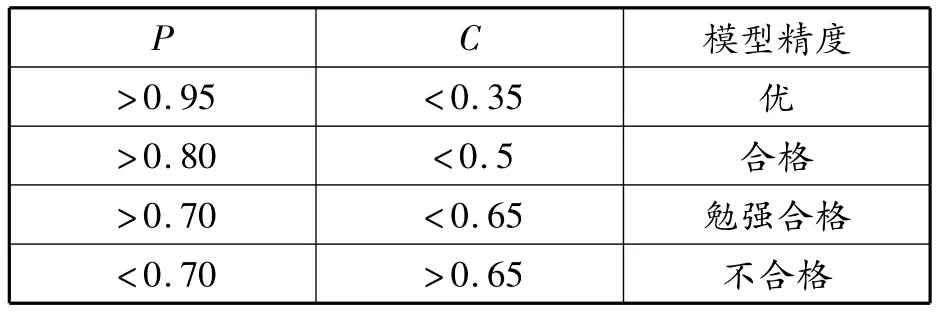
表3 后验差检验判别参照表

(一)房价预测的GM(1，1)模型检验

后验差c=0.322＜0.350，故模型精度为优，可用 ^x(0)(k+1)=5472.65e0.0068k对未来几年的商品房房价进行大致预测。

(二)预测房价的转折点——灾变预测的检验

后验差 c=0.082＜0.35，模型精度为优，故可用 ^q(k+1)=3.41e0.29k进行下一次商品房房价转折点日期预测。

五、结论

房价系统属于灰色系统，通过对郑州市2010年1月—2012年7月商品房房价的实际数据(时间序列)建立GM(1，1)灰色模型，借助Matlab软件，得到了郑州市商品房房价的预测函数 ^x(0)(k+1)=5472.65e0.0068k，并通过后验差检验验证了此预测函数的精确性，进而通过此预测函数对郑州市2012年7月份以后的商品房价格做出分析预测。

在利用GM(1，1)模型建立的商品房价格预测函数基础上进一步建立灾变预测。根据预测结果可以知道，在未来一段时间内郑州市的商品房价总体上有继续上升的趋势，但在上升的过程中会出现小的波动，并且从灾变预测中我们可以得到郑州的商品房价将在2012年12月或2013年1月份左右达到最高点，然后会有所回落。其分析过程对其他相同问题的分析具有一定的参考价值。

［1］姚翠友.基于GM(1，1)模型的北京市房地产投资分析［J］.工业技术经济，2007，26(7):69-72.

［2］张永胜，左祥.2009年房价上涨因素分析及2010年房价走势预测［J］.经济研究导刊，2010(10):136-138.

［3］高成亮，应尚军.房价影响因素系统分析［J］.商场现代化，2009(2):200.

［4］闫妍，许伟，部慧.基于TEI@I方法论的房价预测方法［J］.系统工程理论与实践，2007(7):1-10.

［5］刘大江.灰色—马尔柯夫预测模型在房地产价格预测中的应用［J］.唐山学院学报，2004，17(4):44-46.

［6］刘艺婷.我国商品住房价格的计量经济模型预测研究［J］.企业导报，2009(3):40-42.

［7］龚平.基于BP网络的房地产价格预测［J］.科技创新导报，2008(8):183.

［8］杨华.房价分析模型及对策［J］.武汉工业学院学报，2008，27(1):89-93.

［9］宋成舜，周惠萍.基于灰色系统的西宁市商品房价格影响因素及预测研究［J］.区域经济，2011(5):71-73.

［10］董绪芳，韩树荣.基于GM(1，1)模型对荆州市商品房价格的趋势预测［J］.经济研究导刊，2010(20):69-70.

［11］邓欧，李亦秋.中国房地产价格指数的灰色预测研究［J］.经济研究导刊，2008(7):141-142.

［12］李菲，孙文彬，张军.灰色理论在商品住宅价格预测中的应用［J］.辽宁工程技术大学学报:社会科学版，2004，6(3):271-273.

［13］胡六星，吴结飞.基于灰色系统理论的两种房价预测方法比较［J］.统计与决策，2010(7):22-24.

［14］邓聚龙.灰色系统基本方法［M］.武汉:华中理工大学出版社，1987:12-14.

［15］刘思峰，党耀国，方志耕，等.灰色系统理论及其应用［M］.3版.北京:科学出版社，2004:3-11.

［16］张保法.经济预测与经济决策［M］.北京:经济科学出版社，2004:41-50.

［17］郭斌，李耀丽.西安市房地产市场的发展趋势预测［J］.商场现代化，2008(2):283-284.

［18］孙红湘，沈思.我国房地产开发的灰色预测和分析［J］.西安科技学院学报，2003，23(3):343-346.

［19］王佳.基于时间序列的 GM(1，1)预测模型及应用［J］.统计与决策，2010(19):155-157.

［20］闫海波，陈敬良.地价增长率的 GM(1，1)预测模型［J］.统计与决策，2011(22):168-170.

［21］赖纯见，陈迅.我国住宅销量和价格的主要影响因素——住宅市场宏观调控政策效果分析［J］.重庆工商大学学报:社会科学版，2012(1):37-43.