一种正交局部鉴别嵌入的人脸识别算法

黄 蓓

(东南大学信息科学与工程学院, 南京 210096)

由于人脸属于三维非刚性体对象,因此其图像易受到多种因素的影响,如人脸的相似性、姿态的多样性和光照影响等．传统子空间分析方法[1-8]以所有样本的最优重构为目的,主要衡量不同样本间存在的分类误差,但只能发现全局的欧式结构．当数据呈现高度非线性时,只能描述统计意义下的数据分布．为此,Seung等[9]从神经生理学角度研究了流形学习问题,提出了感知和视觉记忆以流形的形式存在,并从认知学的角度指出图像数据是高维空间中的流形．等距映射(isometric map)[10]和局部线性嵌入(locally linear embedding)[11]2种流形学习算法实现了从高维数据中恢复低维流形结构．而局部保持投影算法(locality preserving projections)[12]将线性映射引入到拉普拉斯特征映射中,实现了线性化投影．此外,提高人脸识别精度还可以通过分类训练的方式实现[13]．

LDE算法[14]不仅利用样本数据间近邻关系来保持局部性,还引入了类别标记信息,其目的是保持其类内紧凑性的同时,增加类间可分性．但该算法同样面临高维小样本问题和致密矩阵的分解问题,需要消耗很大的时间和空间,而谱回归算法能够很好地解决这些问题,因此,本文以LDE算法为基础,提出了相应的修正算法．

1 局部鉴别嵌入的改进算法

1.1 基于谱回归的局部鉴别嵌入算法(SR-LDE)

LDE算法的目标函数为

X(D-W)XTa=λX(DP-WP)XTa

(1)

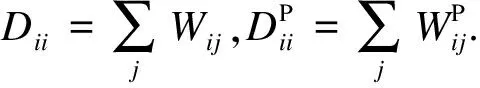
定理1设y是Ly=λBy的特征值λ对应的特征向量,若y=XTa,则a是XLXTa=λXBXTa的广义特征值λ对应的特征向量．

为了使得y=XTa有解,使用正则化最小二乘法对a添加L2范数惩罚项求取近似解:

(2)

式(2)的最优解为:a*=(XTX+μI)-1XTy．其中μ为控制收缩的参数,选择合适的μ值能减小偏差,达到最佳效果．

当μ>0时,a*不能满足线性方程y=XTa,且a不是XLXTa=λXBXTa的特征向量．

定理2若y=XTa是Ly=λBy的特征向量,且y在X的行向量张成的空间,当μ趋于0时,投影向量a是XLXTa=λXBXTa的特征向量．

推论1若y是(D-W)y=λ(DP-WP)y的特征向量,且y=XTa,则a是X(D-W)XTa=λX(DP-WP)XTa对应的特征向量．

证明

X(D-W)XTa=X(D-W)y=
Xλ(DP-WP)y=λX(DP-WP)y=
λX(DP-WP)XTa

式中,y即为高维数据X的低维嵌入．为了得到投影向量a,对方程y=XTa进行分析,并最终采用岭回归方法求解,可得

a*=(XTX+μI)-1XTy

(3)

当μ>0时,式(3)正则解不能满足线性方程y=XTa．

推论2若y=XTa是(D-W)y=λ(DP-WP)y的特征向量,且y在X的行向量张成的空间,当μ趋于0时,投影向量a是X(D-W)XTa=λX(DP-WP)XTa的特征向量．

证明假设rank(X)=r,对X进行奇异值分解,即

X=UΛVT

(4)

式中,Λ=diag(σ1,σ2,…,σr),U∈Rn×r,V∈Rm×r,UTU=VTV=I．y存在于X的行向量张成的空间中,则y也存在于V的列向量张成的空间中．因此,y可以被V的列向量的线性组合所代替．另外,因为V是线性独立的,因此这种组合方式是唯一的．假设组合系数是b1,b2,…,br,b={b1,b2,…,br}T,则

Vb=y⟹VTVb=VTy⟹b=VTy⟹VVTy=y

(5)

(6)

联合式(4),可得

XTa=VΛUTa=VVΛUTUΛ-1VTy=VVTy=y

(7)

所以,a为X(D-W)XTa=λX(DP-WP)XTa的特征向量．

传统的流形学习求解方法是先得到投影向量a,再通过投影向量获得测试数据集X．但该方法是先计算训练样本的特征向量y,然后再通过回归方法计算投影向量a,最后得到测试数据集X．基于上述分析,SR-LDE算法不需要进行n×n维的致密矩阵的特征分解,其特征分解的矩阵为m×m维．在人脸图像中,人脸特征的维数n通常远远大于人脸样本数m,即m≪n,从而有效地降低了算法的复杂性．

1.2 基于谱回归的正交局部鉴别嵌入算法(SR-OLDE)

SR-LDE算法虽然解决了高维小样本应用中矩阵奇异的问题,避免了致密矩阵的分解,但该算法通过求解广义特征值而得到的投影矩阵是非正交的,不利于特征的提取,不能够准确估计高维样本集的内在维数,从而削弱了对测试样本的泛化能力,影响了算法的识别率．为此,本文将求得的低维投影向量进行Gram-Schmidt正交化计算,则不但能够实现正交化约束,且计算简单,易于实现．

假设y={y1,y2,…,yd}是降维后特征值λ={λ1,λ2,…,λd}对应的特征向量,且λ1<λ2<…<λd,d为降维后低维子空间的维数,则SR-LDE算法中求得的投影矩阵为A=[a1,a2,…,ad]．

令b1=a1,设k-1个正交基向量分别为b1,b2,b3,…,bk-1,则第k个向量可根据下式计算:

(8)

尽管B是正交矩阵,但不是单位正交化的标准正交基．因此,要添加约束使其满足BBT=I,则H是主对角元的模均为1的上三角矩阵．

因为原投影矩阵的函数为

(9)

SR-OLDE的正交变换矩阵B=AH,计算JSR-LDE(B)可得

(10)

由上述推导过程可看出,经过施密特正交化操作后,不会改变算法中优化问题的解．B=[b1,b2,…,bd]即为所求的标准正交投影矩阵．

2 实验分析

为了验证本文提出的SR-OLDE算法在人脸识别系统中能够取得良好的效果,采用ORL人脸库进行实验．实验环境为Pentium Dual-Core CPU E5400,主频2.70 GHz,2GB内存．设μ=0.01.下面通过比较SR-OLDE算法和PCA,LDA,LPP,LDE,SR-LDE算法的实验效果,来展现SR-OLDE的性能．

2.1 ORL人脸库上的实验结果

ORL人脸库由剑桥大学AT&T实验室创建,包括40个人,每人10幅,共400幅面部图像,其中有些人脸图像是在不同时期拍摄的．ORL人脸库中每个人的不同图像均具有不同的表情和面部细节,如笑或不笑,戴或不戴眼镜,眼睛睁开或闭着．所有图像均是大致正面图像(部分侧转旋转角度不超过20°),人脸尺度变化不超过10%,每幅图像的分辨率为92×112像素．在本实验中,所有图像的大小均被归一化至64×64像素．

实验时,随机选取每个人的G(G=2,3,4,5)幅图像作为训练集,其余10-G个样本作为测试集,为了消除随机因素的影响,对每个选定的G,其随机选择过程都重复10次,且每次实验相互独立,实验的最终结果是这10次实验所取的平均值．针对不同训练样本数,各种算法的最优实验结果如表1所示．由于在不同训练样本数和测试样本数时算法识别率和维数之间的关系是类似的,因此本文选择G2/P8(G2/P8表示训练样本数为2,测试样本数为8)绘制维数和识别率之间的关系图,如图1所示．

表1 不同训练样本时的各算法人脸识别率 %

图1 不同算法的识别率与维数间的关系

2.2 实验结果分析

由以上实验结果分析可知,无论是传统的子空间降维算法,还是流形学习算法,随着测试样本数量的增加,各种算法的识别率都提高了,而流形学习算法较传统降维方法取得了更好的识别效果．本文SR-OLDE算法的实验效果最好,因为它使用谱回归算法求解,在解决小样本问题的同时避免了致密矩阵的分解,另外,又采用Gram-Schmidt正交方法实现了投影矩阵的正交化,从而提高了识别率．

传统的图嵌入算法在处理大规模高维数据集时,通常由于计算复杂度较高,不宜直接应用,而谱回归算法的提出可以避免致密矩阵的分解,有效地解决了大规模高维数据集的广义特征值问题,从而缩短了计算时间．ORL人脸库不同训练样本数所需的训练时间如表2所示．其中,SR-OLDE算法训练所需时间比SR-LDE所需时间长,这是因为进行正交化计算需要一定的计算时间．

表2 不同训练样本数所需训练时间 s

3 结语

在人脸识别过程中,由于流形学习算法比传统的子空间降维算法具有更好的识别效果,因此本文选择LDE算法作为研究对象．为改善LDE算法的高维小样本泛化能力弱和致密矩阵分解计算量大等问题,首先通过引入谱回归算法,提出了SR-LDE算法．然后,考虑到投影向量若非正交,则不利于特征提取和准确估计高维数据集的内在维数,从而削弱了测试样本的泛化能力,影响识别率,因此,将Gram-Schmidt正交化方法引入到SR-LDE算法中,提出了SR-OLDE算法．最后,将改进的算法在ORL人脸库中进行测试．实验结果证明,SR-OLDE算法在识别率和计算速度方面都取得了比较好的效果．

)

[1] Wiskott L, Fellous J, Kruger N, et al. Face recognition by elastic bunch graph matching[J].IEEETransactionsonPatternAnalysisandMachineIntelligence, 1997,19(7): 775-779.

[2] Kumar P P, Vadakkepat P, Loh A P. Graph matching based hand posture recognition using neuro-biologically inspired features[C]//11thInternationalConferenceonControlAutomationRoboticsandVision. Singapore, 2010:1151-1156.

[3] Kshirsagar V P, Baviskar M R, Gaikwad M E. Face recognition using Eigenfaces[C]//3rdInternationalConferenceonComputerResearchandDevelopment. Shanghai, China, 2011:302-306.

[4] Huang S M, Yang J F. Subface hidden Markov models coupled with a universal occlusion model for partially occluded face recognition[J].IETBiometrics, 2012,1(3):149-159.

[5] Du S, Shehata M, Badawy W. A novel algorithm for illumination invariant DCT-based face recognition[C]//25thIEEECanadianConferenceonElectricalandComputerEngineering. Montreal, QC, Canada, 2012:1-4.

[6] Maria D M, Michele N, Daniel R, et al. Robust face recognition for uncontrolled pose and illumination changes[J].IEEETransactionsonSystems,Man,andCybernetics:Systems, 2013,43(1):149-163.

[7] He Y, Jin B, Yang S. Improving BP neural network for the recognition of face direction[C]//InternationalSymposiumonComputerScienceandSociety. Kota Kinabalu, Malaysia, 2011:79-82.

[8] Jing X Y, Sun J, Yao Y F, et al. Supervised and unsupervised face recognition method based on 3CCA[C]//InternationalConferenceonAutomaticControlandArtificialIntelligence. Xiamen, China, 2012:2009-2012.

[9] Seung H S, Lee D D. The manifold ways of perception[J].Science, 2000,290(5500): 2268-2269.

[10] Tenenbaum J B, de Silva V, Langford J C. A global geometric framework for nonlinear dimensionality reduction[J].Science, 2000,290(5500): 2319-2323.

[11] Roweis S T, Saul L K. Nonlinear dimensionality reduction by locally linear embedding[J].Science, 2000,290(5500):2323-2326.

[12] He X F, Yan S C, Hu Y X, et al. Face recognition using Laplacianfaces[J].IEEETransactionsonPatternAnalysisandMachineIntelligence, 2005,27(3):328-340.

[13] Brenda F K, Mark J B, Joshua C K, et al. Face recognition performance: role of demographic information[J].IEEETransactionsonInformationForensicsandSecurity, 2012,7(6):1789-1801.

[14] Chen H T,Chang H W, Liu T L.Local discriminant embedding and its variants[C]//IEEEComputerSocietyConferenceonComputerVisionandPatternRecognition. San Diego, CA, USA, 2005: 846-853.