基于时间触发多传感器融合的列车测速定位系统可调度性
马维纲 马建峰 黑新宏 曹 源
(1西安电子科技大学计算机学院,西安 710071)
(2西安理工大学计算机科学与工程学院,西安 710048)
(3北京交通大学电子信息工程学院,北京 100044)
列车运行控制系统(列控系统)是安全苛求系统.列车测速定位系统是列控系统的重要组成部分,其向列控系统输入的位置和速度参数需要具备严格的精度、可靠性和实时性.多传感器融合的测速定位是利用不同传感器的优势,为系统提供更可靠精确的信息.传感器包括陀螺、电子罗盘、加速度计、速度传感器、惯性测量单元、多普勒雷达、GPS接收机等.
多传感器融合系统中传感器信号输入由外部环境实时状态触发.对于多传感器融合系统需采用多任务实时调度.实时调度有事件触发和时间触发2种方式.在测速定位系统中时间触发有确定性的优势,能更好地保证实时系统安全性,在列车测速定位系统中得到了广泛的应用.时间触发机制是将时间轴分割成若干窗口,采用人为分配方式,已知任务执行时间、截止时间等信息进行时间窗分配,得到静态时间调度表,并在静态表中分配一定时间窗来调度非实时任务,在时标间隔到达时进行超时检测并进行超时处理.人为分配具有不确定性,故时间触发机制的调度分析尤为重要.
文献[1]基于单处理器的嵌入式系统,提出基于能效和公平的调度算法,结果显示该算法能够减少能量消耗,但降低了处理器的运算速度.文献[2]提出一种基于调度表的自适应任务分配调度算法,结果显示该算法能够提高系统的响应.文献[3]提出一种基于CTCS-3列控系统的高层数据融合方法,实现了列控系统关键数据的融合,提高了列控的安全性.
Liu等[4]提出一种适用于抢占式实时周期任务调度的调度算法,并对其可调度性判定进行研究.Nicolau[5]针对固定优先级可抢占任务调度给出了任务请求调度时间计算公式,公式计算量小,计算结果误差较大.Henderson等[6]给出了截止时间不大于调度周期约束下实时任务调度响应时间的计算方法,此方法复杂度较高.Lehoczky等[7]提出了一种通用的实时任务响应时间分析方法,该方法通过时间需求分析对调度模型作了一系列理想的假设,使理想的调度模型比现实情况要简单.Katcher等[8]提出的可调度分析方法利用最坏响应时间进行分析,能作为充分判定条件,不能用于相同优先级任务在初始执行顺序确定约束条件下的调度分析.伍微等[9]在此基础上提出了优先级相同的任务在初始执行顺序确定的条件下的调度算法.
以上研究均考虑了任务抢占的情况,但是时间触发机制采用固定优先级,故本文研究的是在任务调度顺序确定的约束下采用的调度方法.首先,实时系统必须具备处理外部事件的功能,这些外部事件随机发生;其次,为避免任务因挂起导致未完成执行,需要在每个时标间隔到达时进行超时检测.
因此,本文在简化假设条件下,考虑到调度系统应具备处理外部事件的功能和执行超时检测的功能,提出多传感器融合测速定位系统的调度模型,并在任务时间需求函数基础上计算系统消耗时间和CPU利用率,提出了关于时间触发机制可调度性的判定定理,从而为时间触发静态调度表的分配提供合适的参数,在保证时间触发机制安全性基础上,提高系统利用率.
1 基于时间触发机制的多传感器融合系统模型
调度器通过硬件定时器实现,硬件定时器被设置为产生一个周期中断信号,中断周期又称作时标间隔.列车测速定位系统包括2个部分:数据采集和数据处理.数据采集通过不同串口完成多个传感器数据采集任务;数据处理将采集数据融合处理,得到速度和定位信息.系统对传感器信号有不同的需求,大部分传感器的信号获取、数据处理与输出均是实时周期任务,少量传感器信号的获取是软实时非周期任务.
1.1 实时周期任务模型
设多传感器融合系统的实时周期任务集为
Γ={τi|1≤i≤n}
式中,n为系统中的周期任务数;τi为第i个任务,τi={φi,Ci,Ti,Di},其中,φi为初始就绪时刻,Ci为任务i的执行时间,Ti为任务i的周期,Di为任务i的截止时间,即任务i的最大允许响应时间.
对于任务集Γ中的各个任务τi,其周期Ti并不相同.系统周期由这些基本循环周期构成,称为超周期H.时标间隔I选择为能够整除系统超周期H,因此I应为各任务周期的公约数,且至少存在i,使I至少可以被任务Ti的周期Ti整除,即⌊Ti/I⌋-Ti/I=0.
1.2 软实时非周期任务模型
系统中软实时非周期任务是随机发生的,其在超周期H内发生的概率用分布函数P(x)模拟.定义软实时非周期任务为
pj={φj,Cj,Dj}
式中,φj为任务初始就绪时刻,由概率分布函数P(x)决定;Cj为任务j的执行时间;Dj为软实时非周期任务j的截止时间.
超周期中的实时周期任务调度结束后,需要预留一定冗余时段为动态段,此段定义为l,用于软实时非周期性任务的调度.
1.3 超时检测模型
时间触发机制在时标间隔到达时进行任务超时检测,如果此时有任务运行,则该任务由于某些因素未被执行完毕,需要进行超时处理.
本文只考虑超时检测任务,而不考虑具体的超时处理方式.定义超时处理任务集为
O={ok|1≤k≤n}ok={co,I}
式中,co为超时检测需要的时间;I为定时器的中断时间.
图1为时间触发机制调度算法的实现框图.

图1 基于时间触发机制的调度策略
2 时间触发机制可调度性分析与验证
首先作如下假设:
1) 实时周期任务请求都具有硬时限要求,必须在限定的时限内完成.
2) 软实时非周期任务没有硬时限要求,在动态段l调度,采用固定优先级调度算法.
3) 任务在运行中不会被其他任务打断,但可被定时器中断.
4) 每个任务的运行时间恒定.
5) 调度和任务切换的时间忽略不计.
定理1对实时周期任务集Γ={τi|1≤i≤n}中的任务Ti,保证其在释放后能够在截止时间前得到调度,即满足
φi+Ci≤φi+Di≤φi+1
(1)
则此任务可以调度.
证明在基于时间触发机制的系统中,任务基于已确定的调度表调度,任务优先级已确定,其释放时间到达就可以得到调度,任务的执行时间Ci即任务响应时间Wi(t),是从任务释放到完成的时间.只需在任务释放时满足Wi(t) 定理2对软实时非周期任务集P={pj|1≤j≤n},任务释放并在超周期结束前完成调度,则此任务即可调度.对任务集P,其在动态段内按照固定优先级在调度表中进行排列,假设任务pj在时刻t调度并完成,实现调度需满足t 其中 u′(k)=1的概率为 p(u′(k)=1)=P(φ(k)≤t) (2) 证明略. 在调度过程中必须保证实时周期任务能够满足时限约束的条件.任务调度处理过程是先调度实时周期任务,再考虑调度软实时非周期任务.软实时非周期任务以一定的概率得到调度. U=UΓ+UP+Uo+Uc≤1 (3) 定理4对于实时周期任务集Γ={τi|1≤i≤n},任意时刻t运行的任务为τi,任务集在[0,t]间的总响应时间为 其中 对超时检测段,其响应时间为 对动态段,t时间内动态段占用的时间为 其中 令W(t)=WΓ(t)+Wo(t)+tl,L(t)=W(t)/t,任务集可调度当且仅当 L(t)≤1 (4) 对整个任务集,保证每个实时周期任务和超时检测任务在非动态段调度,则系统即可实现调度,即W(t)=WΓ(t)+Wo(t)≤t-tl,令L(t)=W(t)/t,则L(t)≤1,定理得证. 为验证基于时间触发机制的多传感器融合测速定位系统的可调度性,在济南至连云港铁路区段进行了现场实验,获得了有效的数据信息,验证了系统的功能.实验的任务参数如表1所示. 表1 系统任务参数 ms 表1中,任务1,2,3,4,5,7,8为实时周期任务;任务6为软实时非周期任务;任务9为超时检测任务.系统采用时间触发方式实现对任务的调度.时标间隔I取50 ms,超周期为1 000 ms. 对于定理1,各实时周期任务均满足条件φi+Ci≤φi+Di≤φi+1(1≤i≤9).定理3中,假设任务调度产生的CPU消耗为10%,Uo=c9/I,UP=c6/H,UΓ=U1+U2+U3+U4+U5+U7+U8,则系统总的利用率为U=UΓ+UP+Uo+Uc=0.66≤1,满足定理3.假设1 000 ms时间内,任务集总响应时间W(t)=595 ms,L(t)=W(t)/t=595/1 000=0.595<1,满足定理4. 在轨检车的数据采集和测试过程中,基于时间触发机制的多传感器融合测速定位系统能正确获取传感器数据,并在规定的时刻能正确输出列车位置和速度信息,且系统运行状况良好. 本文讨论了基于时间触发机制的多传感器融合测速定位系统的调度模型,建立了系统中的实时周期任务、软实时非周期任务和超时检测任务模型,在任务时间需求函数的基础上,计算系统消耗的时间和CPU利用率,提出了关于时间触发机制的可调度性判定定理.通过判定定理可以改进时间触发静态调度表的设计,为调度表分配更合理的参数,从而在保证时间触发机制的可预测性和安全性基础上提高系统的利用率.最后通过具体的实验分析,验证了将时间触发机制用于此系统中是可行的.后续工作将考虑优化时间触发调度策略,进一步提高系统的利用率. ) [1] Rukpakavong W, Bull P, Guan Lin,et al. Energy efficient and fairness scheduling of periodic real-time tasks for wireless embedded systems [C]//Computing,CommunicationsandITApplicationsConference. Hong Kong, China, 2013: 111-114. [2] Ahmed S, Ferri B. Prediction-based asynchronous Cpu-budget allocation for soft-real-time applications[J].IEEETransactionsonComputers. (to appear) [3] 王俊峰,汪希时. CTCS-3列车控制系统数据融合方法研究[J].铁道学报, 2012,34(9): 70-74. Wang Junfeng,Wang Xishi. Research on data fusion of CTCS-3 train control system [J].JournaloftheRailwaySociety, 2012,34(9): 70-74. (in Chinese) [4] Liu C L, Layland J W. Scheduling algorithms for multiprogramming in a hard real time environment[J].JournalofACM, 1973,20(1): 46-61. [5] Nicolau G B. Specification and analysis of weakly hard real-time systems [D]. Islas Baleares, Spain: Department de Ciencies Matemaytique I informatica, Universitat delesllles Barlears, 1998. [6] Henderson W, Kendall D, Robson A. Improving the accuracy of scheduling analysis applied to distributed systems: computing minimal response times and reducing jitter [J].InternationalJournalofReal-TimeSystems, 2001,20(1): 5-25. [7] Lehoczky J P, Sha L, Ding Y. The rate monotonic scheduling algorithm: exact characterization and average case behavior[C]//Proceedingsofthe10thIEEERealTimeSystemsSymposium. Santa Monica, CA, USA, 1989: 166-171. [8] Katcher D I, Sathaye S S, Strosnider J K. Fixed priority scheduling with limited priority levels[J].IEEETransactionsonComputers, 1995,44(9): 1140-1144. [9] 伍微,倪少杰,刘小汇.优先级受限系统中可调度判定方法[J].计算机工程与应用,2009,45(5):32-35. Wu Wei, Ni Shaojie, Liu Xiaohui. Schedulability analysis of fixed priority systems with limited priority levels[J].ComputerEngineeringandApplications, 2009,45(5): 32-35. (in Chinese) [10] Pont M J.Patternsfortimetriggeredembeddedsystems:buildingreliableapplicationswiththe8051familyofmicrocontrollers[M]. Addison-Wesley, 2001: 53-55.
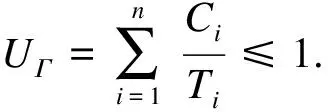

3 多传感器融合测速定位系统可调度性判定

4 结语

