基于FSAGE的OFDM系统信道与频偏联合干扰消除算法

李玉峰 关庆阳 沈连丰

(1东南大学移动通信国家重点实验室,南京 210096)

(2沈阳航空航天大学电子信息工程学院,沈阳 110136)

正交频分复用(OFDM)作为多载波的调制方式,能充分利用频谱资源,有效抵抗频率选择性干扰,并且收发机结构简单,已被公认为是下一代高速无线通信系统的主要物理层解决方案之一.目前,OFDM已被诸多无线通信标准采纳,如数字音频广播(DAB)、无线局域网(WLAN)、无线城域网(wireless metropolitan area network, WMAN)、长期演进(LTE)等.信道与频偏联合干扰消除是实现OFDM技术的一个关键问题.信道与频偏联合干扰消除算法可分为有辅助符号的非盲干扰消除算法、无辅助符号的盲干扰消除算法以及半盲干扰消除算法.有辅助符号的非盲干扰消除算法能在慢变信道下获得较小的误差,适合慢变信道的无线通信系统,其缺点是引入辅助的符号会降低系统的有效数据传输率.盲干扰消除算法节约了信道带宽,极大地提高了系统的有效数据传输效率,并且能更好地跟踪无线通信的变化,但运算量较大,收敛时间长,且性能在达到一定程度后不随SNR的提高而相应改善,因此阻碍了它在实际系统中的应用.半盲干扰消除是在数据传输效率和收敛速度之间进行折中,即采用较少的训练序列来获得信道的信息.

针对信道与频偏联合干扰消除问题,早期文献中,ML(maximum likelihood)算法作为经典的信道及频偏联合干扰消除算法而得到了广泛应用.但当接收信号的估计量统计特性复杂且被估计参量较多时,算法的性能并不理想.文献[1]采用EM(expectation-maximization)算法以迭代形式实现某些无法获知的参数估计,结果表明EM算法具有相对较低的实现复杂度,并且每次迭代可获得良好的收敛性.文献[2-5]将EM算法用于OFDM系统中,文献[4]在时域完成信号检测,文献[5]在频域来检测信号,并与SISO译码器结合,可以有效地提高系统性能.文献[6]利用EM算法将载波频偏和信道冲击响应反复迭代来提高信道及频偏联合干扰消除性能,文献[7-11]将信道及频偏的联合干扰分解成若干个部分,分别估计各个部分所包含的参数,通过前向和后向迭代以逼近信道及频偏的真实值,但由于EM算法在每一次迭代时需要同时对所有的参数进行更新,因此收敛速度较慢.

针对OFDM系统信道及频偏联合干扰消除问题,为了降低接收端的算法复杂度及处理时延,需要减少迭代次数,消除干扰以提高用户信号检测精度.因此,本文提出一种信道及载波频偏联合干扰消除的频域空间选择性期望最大化(FSAGE)算法.

1 系统模型

图1给出OFDM传输体制原理框图.OFDM通过串并转换把高速串行数据流通过正交子载波进行传输,以N个子载波的OFDM系统为例,各子载波的速率变为原传输速率的1/N,使得子载波的传输符号持续时间增加,每个子载波的信道频率响应特性变为平坦.

图1 OFDM传输框图

设定一个OFDM符号周期为T,将子载波进行排序后,序号最低的子载波传输频率为f0.则子载波的间隔选取为1/T,第i个子载波的频率为fi=f0+i/T,其中,i=0,1,2,…,N-1.则发送端的一个OFDM符号可表示为

(1)

将DFT应用到传输系统的调制/解调部分,并且采用FFT来实现.对信号x(t)进行1/Ts采样,得到

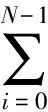
(2)

设定一个码元内包括N个样值,令f0=0,得到

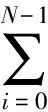
(3)

OFDM系统为了降低符号间干扰(ISI),并且对抗信道多径扩展时延,在每个OFDM符号之间插入大于最大扩展时延的保护间隔;同时为了消除多径信道引入的子载波间干扰(ICI),在保护间隔内加入循环前缀.

令x(n)为OFDM发送的时域信号,ξ为相对频偏干扰因子,h(n,l)为L径信道冲击响应,则接收端时域信号y(n)可表示为

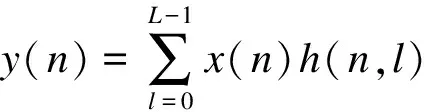
(4)

引入频偏干扰后,接收信号变为

(5)

OFDM系统中叠加高斯白噪声后的接收信号可表示为

y(n)=x(n)+z(n)

(6)

式中,z(n)为功率谱密度是N0/2,均值是0的加性高斯白噪声.

2 信道及频偏联合干扰消除算法

如果用户处于建筑物多、遮挡严重场景时,折射、绕射严重,信道条件较差,因此用户终端信号干扰不仅仅由频偏造成,还包括信道严重多径衰落.针对此类服务场景,需要对信道以及频偏联合干扰进行消除.

文献[12-13]提出了基于空间分解的SAGE (space-alternating generalized expectation-maximization)算法.文献[14]采用SAGE算法,并将上述EM算法中复杂的多维迭代简化为一维迭代,降低了算法实现复杂度;与EM算法不同的是,SAGE算法每次迭代仅更新部分参数,提高了其收敛速度与估计精度.但是SAGE算法的信道与频偏联合估计需要的迭代次数很高,这主要是由于频偏初始值的误差很大.

为了降低频域处理的迭代次数及复杂度,提高SAGE算法的性能,本文提出了联合信道及频偏干扰消除的FSAGE算法,算法的实现框图如图2所示.

图2 FSAGE算法的实现框图

FSAGE算法通过对频域载波频偏进行预估计及消除来降低频域联合干扰消除的迭代次数,提高频偏及信道的联合跟踪性能.带有频偏干扰的信号经过DFT变换到频域后,首先在频域内进行频偏的粗估计,然后将估计的频偏值反馈到时域.当频偏干扰较小时,经过粗消除后的信号能够满足通信的需求;但当信道多径衰落严重,频偏干扰较大时,需要采用SAGE算法实现频偏及信道的联合跟踪.

令N为系统子载波数目,则移动用户终端接收的频域信号Y(k)可表示为

Y(k)=X(k)H(k)C(0)+

(7)

式中,H(k)为信道频域响应;Z(k)为高斯白噪声频域响应;载波干扰项C(l-k)可表示为

(8)

经DFT变换后,写成如下矩阵形式:

R(k)=X(k)H(k)C+Z(k)

(9)

式中,C为频偏干扰矩阵,即

对该矩阵的首项做如下处理:首先按照最小二乘估计准则获得频偏干扰估计矩阵,即

(11)

然后获取估计的干扰矩阵首项,对矩阵首项进行频偏粗估计,得到

(12)

信号经过频偏干扰预消除及DFT变换后,接收的频域信号表示为

y=Γ(ε)FD(x)wh+z

(13)

(14)

式中,0≤p,q≤N-1;w为信道冲击响应的DFT变换因子,

(15)

其中,0≤l,m≤L-1.

按照ML准则,得到似然函数为

(16)

(17)

(18)

其中

(19)

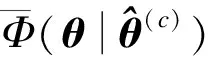
(20)

式(20)的第c+1次迭代后的最优解可表示为

(21)

其中

(22)

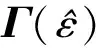
(23)

(24)

对于所有参数加以更新,第c+1次更新值为

(25)

FSAGE算法首先选定合适的频偏预消除后的迭代初值ε(0)以及信道频域响应初值h(0),以便加快收敛速度、保证全局收敛,并且通过训练序列获得信道冲击响应估计作为初始信道迭代初始值.在后续的信道及频偏跟踪阶段,将每次迭代的结果作为当前信号信道冲击响应以及载波频偏值.在进行频偏及信道跟踪时,需要设置门限来终止迭代,当系统误差小于预设门限则认为是收敛,停止算法迭代.

3 仿真结果及分析

载波频率采用L波段,链路信号传输比特率为40 Mbit/s,仿真信道模型采用具有直射分量的5径城区信道模型,主径服从Rician分布,多径扩展延时为60,100,130 ns,最大扩展延时为250 ns.系统采用的载波数目为512,并且采用的循环前缀长度大于信道多径的扩展延时,信号映射为QPSK,Eb/N0=20 dB.为了便于分析,系统子载波的相对频偏因子ξ为0.25,频偏预消除检测门限的相对频偏因子为0.01.

图3(a)是QPSK信号的星座图,包含未被消除的信道以及载波频偏的干扰,由图可见,发送的信号完全淹没在干扰信号中.图3(b)为经过频偏预消除后的星座图仿真,可看出系统性能有所改善,但干扰信号仍然很强,这些干扰主要是残留频偏以及信道多径衰落引入的干扰.图3(c)为经过一次迭代后的星座图仿真,从仿真图看出,系统性能有所改善,但是还不能完全消除频偏干扰与信道衰落引入的干扰,所以算法性能没有达到最优.图3(d)是经过2次迭代后的星座图,可看出经过联合信道及频偏干扰消除后的星座图可以达到最优值,系统性能也得到较大改善.

图4是FSAGE算法的误码率(BER)仿真图.从图中可看出,没有经过信道均衡以及频偏消除时,算法的误码率性能最差,主要原因在于解调信号质量太差,星座解映射已经完全无法辨认原有信息,随着信噪比的增加,信号的解码特性并没有得到较多改善;经过频偏预消除后,误码率性能稍微有些改善,这主要是由于频偏干扰预消除并不能完全消除干扰,残留频偏以及信道衰落的干扰也较大.经过第1次迭代消除后,算法的误码率得到大幅度改善,经过初次分离的频偏干扰以及信道衰落干扰可以分别消除;经过2次迭代后,算法可以较好地消除频偏以及信道带来的干扰,频偏的估计也更接近真实值,所以误码率曲线性能接近最优值.

图3 FSAGE算法对QPSK信号的处理结果 (ξ=0.25)

图5给出了信噪比分别为10 dB和20 dB时,移动用户终端信号检测采用本文提出的FSAGE算法与文献[14]提出的SAGE算法的迭代次数比较.可看出,经过频域频偏粗消除后,FSAGE算法减少了后端跟踪算法的迭代次数,降低了算法处理时延,提高了信号处理效率.信噪比为20 dB时,FSAGE算法大致需要5次迭代能够获得期望性能;而传统的SAGE算法需要10次左右迭代,因此FSAGE算法的信号处理性能(均方误差MSE)相比SAGE算法有较大提升.

图4 不同迭代次数的FSAGE算法误码率性能

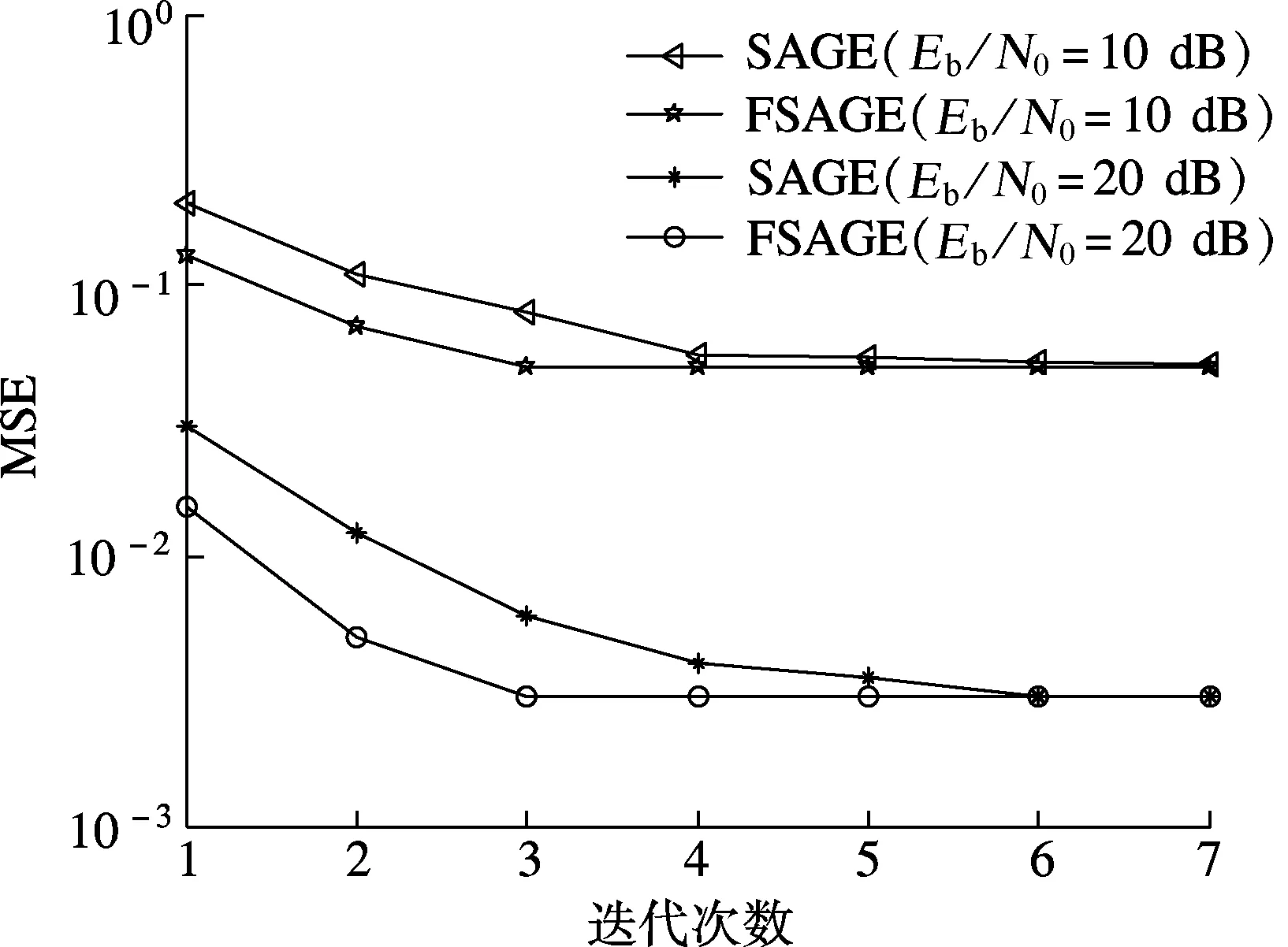
图5 不同迭代次数的FSAGE算法与SAGE算法的收敛性能比较

4 结语

针对OFDM系统信道衰落严重的场景,提出联合信道与频偏干扰消除的FSAGE算法.为了减少信道干扰与频偏干扰迭代次数,首先进行频域频偏预估计及消除，然后进行信道及频偏联合干扰的跟踪及消除.从仿真结果可看出,该算法能够降低信道与频偏干扰消除算法的迭代次数和处理时延,有效地消除由于信道多径衰落以及频偏引入的联合干扰.

)

[1] Ma X, Kobayashi H, Schwartz C. EM-based channel estimation algorithms for OFDM[J].EURASIPJournalonAppliedSignalProcessing, 2004,2004(10):1460-1477.

[2] Mazet L, Buzenac S V, Courville D, et al. An EM based semi-blind channel estimation algorithm designed for OFDM systems [C]//IEEEInternationalConferenceonSignals,SystemsandComputers. Pacific Groove, CA, USA, 2002,2: 1642-1646.

[3] Jain S, Gupta P, Mehra D K. EM-MMSE based channel estimation for OFDM systems[C]//IEEEInternationalConferenceonIndustrialTechnology. Bhubaneswar, Orissa, India, 2006: 2598-2602.

[4] Ocloo J M, Alberge F, Duhamel P. Semi-blind channel estimation for OFDM systems via an EM-MAP algorithm[C]//IEEEInternationalConferenceonSignalProcessing. New York, 2005: 605-609.

[5] Lee J H, Han J C, Kim S C. Joint carrier frequency synchronization and channel estimation for OFDM systems via the EM algorithm[J].IEEETransactionsonVehicularTechnology, 2006,55(1):167-172.

[6] Feder M, Weinstein E. Parameter estimation of superimposed signals using the EM algorithm[J].IEEETransactionsonAcoustics,SpeechandSignalProcessing, 1988,36(4): 477-489.

[7] Ma X Q, Kobaya S H, Schwartz S C. Joint frequency offset and channel estimation for OFDM[C]//IEEEInternationalConferenceonGlobalTelecommunications. San Francisco,CA,USA, 2003,3: 15-19.

[8] Pun M O, Tsai S H, Kuo C C J. An EM-based joint maximum likelihood estimation of carrier frequency offset and channel for uplink OFDMA systems[C]//IEEEInternationalConferenceonVehicularTechnology. Washington, USA, 2004,1: 598-602.

[9] Mo R H, Chew Y H, Ko C C, et al. An EM-based semiblind joint channel and frequency offset estimator for OFDM systems over frequency-selective fading channels[J].IEEETransactionsonVehicularTechnology, 2008,57(5): 3275-3282.

[10] Morelli M, Sanguinetti L. Estimation of channel statistics for iterative detection of OFDM signals[J].IEEETransactionsonWirelessCommunications, 2005,4(4): 1360-1365.

[11] Xu P, Wang J K, Qi F. A novel EM-based MAP channel estimation for MIMO-OFDM systems[C]//IEEEInternationalConferenceonNetworking,SensingandControl. Chicago, IL, USA, 2010: 58-61.

[12] Panayrc E, Senol H, Poor H V. Joint data detection and channel estimation for OFDM systems in the presence of very high mobility[C]//IEEEInternationalConferenceonPersonal,IndoorandMobileRadioCommunications. Tokyo, Japan, 2009: 461-465.

[13] Lee J H, Kim S C. Residual frequency offset compensation using the approximate SAGE algorithm for OFDM system[J].IEEETransactionsonCommunications, 2006,54(5): 765-769.

[14] Lee J H, Kim S C. Time and frequency synchronization for OFDMA uplink system using the SAGE algorithm[J].IEEETransactionsonWirelessCommunications, 2007,6(4): 1176-1181.