制导工具误差分离自适应正则化模型及应用

王文君，段晓君，朱炬波

（国防科学技术大学 理学院，长沙410073）

制导工具误差分离作为评估惯性导航设备性能和验证天地一致性的主要手段，在国内已经有近30年的研究历史。文献［1］在国内最早提出了制导工具误差分析一般思想和基于协方差的分析方法。文献［2］提出利用特殊弹道估计得到的误差系数，并将其作为验前信息，结合Bayes估计理论推算正常弹道误差系数的方法。文献［3］将制导工具误差系数分离问题归为线性回归问题，建立了线性分离模型并提出了主成分分析方法。文献［4］从制导工具误差的数据检验出发，重点讨论了利用先验信息和不利用先验信息的两类方法，给出了各自的适用范围。文献［5］针对特定的惯导系统，即速率捷联制导系统进行了数值仿真和计算。文献［6］提出了制导系统工具误差在特殊弹道和全程弹道之间的折合方法。文献［7］针对线性模型给出了基于假设检验的误差系数评价方法。文献［8］对遥外测数据的互校准进行了专题论述，对于细节问题如环境函数的精确计算等展开了详细的讨论。

本世纪初，国内相关领域的科研工作者对于制导工具误差分离的模型和方法均进行了更为广泛和深入的研究。模型方面，先后提出了误差分离的非线性模型［9－10］，基于 Bayes的多层先验模型［11］，文献［12］对误差分离线性模型的稀疏选择做了初步的讨论，并比较了正则化迭代算法与主成分分析方法的仿真计算结果。算法方面，先后提出了基于SVM和最优 LS－SVM 的误差分离方法［13－14］、基于遗传算法和遗传主成分分析的误差分离算法［15－16］，特征根估计算法［17］和比定阶行列式方法［18］等。

在不考虑直接融合地面测试先验信息的情况下，线性模型的主要分离方法是以主成分分析为核心的一类方法。不过主成分的项数选取与数据有关，很难给出一个普适性的原则。若对制导工具误差分离提出更高的精度要求，则研究新的分离方法势在必行。由于制导工具的所有误差项中存在主次之分，即起决定性作用的仅有其中部分项。从数学的角度理解，制导工具误差系数在某种程度上存在着稀疏性。利用稀疏性对线性模型加以约束，有望克服原问题的病态性［19－20］。

本文拟从误差分离的线性模型入手，深入讨论基于稀疏先验约束的正则化误差分离模型，提出自适应参数正则化误差分离模型，同时给出相应的求解算法，最后结合试验结果对几种算法作出评价。

1 线性分离模型及经典解法

1.1 线性分离模型

考虑速度域制导工具系统误差的线性模型［1－3］：

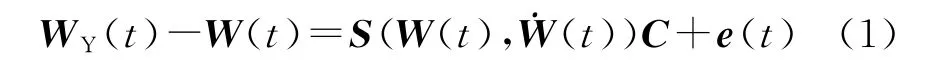
式中：WY（t）为某采样时刻遥测视速度向量（3个方向）；W（t）为惯性系下真实视速度向量（3个方向）；S（W（t），（t））为速度域环境函数矩阵；C为待估误差系数向量；e（t）为误差向量。

通常情况下，惯性系下真实的视速度无法得知，一般采用精度较高的外转遥数据WW2Y（t）代替W（t），故式（1）可化为

式中：下标Y表示遥测坐标系，下标W表示外测坐标系，下标W2Y表示外测坐标系数据向遥测坐标系转换。模型（2）可简记为

式中：e′包含了表示误差e和采用WW2Y（t）数据引入的转换误差，通常可以认为e′～N（0，σI3）。故此，模型（3）的最小二乘解为

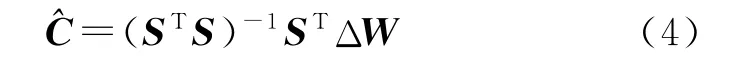
由于环境函数S的各列之间存在较强的相关性［3］，故此矩阵STS是病态的，根据式（4）求得的最小二乘解并不准确。为克服矩阵STS的病态性，通常采用比例因子规范化和主成分分析2种方法。

1.2 比例因子规范化

对线性回归模型ΔW＝SC＋e′，当STS呈病态时，最小二乘估计的均方误差的值很大，从而导致最小二乘的估计效果差。设Q是一个已知的非奇异矩阵，且满足QQ－1≡I。将上述回归模型改写为

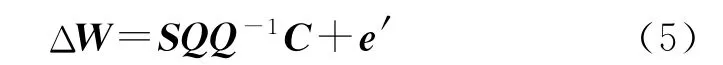
令V＝ΔSQ，a＝ΔQ－1C，则模型转化为

若由此模型得到估计，则易知＝是C的一种估计。规范化后的矩阵V使得原矩阵S的病态性得以减弱，而Q被称为规范化比例因子。

选择合适的Q可使得估计具有较高的效率，具体可从以下3个方面考虑：①根据工程物理背景确定Q；②根据先验测试值确定Q，例如在制导工具系统误差分离中，可采用制导工具系统误差系数的地面测试值；③根据工程经验获得Q，对于一个确定的问题，可以通过工程经验确定哪些列之间是线性相关的，或者对模型影响小，从而选取相应的比例因子。

1.3 主成分分析方法

针对问题（3），记λ1≥λ2≥…≥λm为矩阵STS的m个特征根；记V1，V2，…，Vm为λ1，λ2，…，λm对应的标准正交化特征向量，令V＝（V1V2…Vm）；记Z＝SV，a＝VTC，记Y＝ΔΔW′t，则式（3）可化为

进一步，a的最小二乘估计为

注意到（diag（λ1，λ2，…，λm））－1，如果当i＞k时有λi＝0或λi≈0，则λk＋1，λk＋2，…，λm对矩阵求逆运算没有影响或影响很小；而λ1，λ2，…，λk对矩阵求逆运算影响很大，故此有

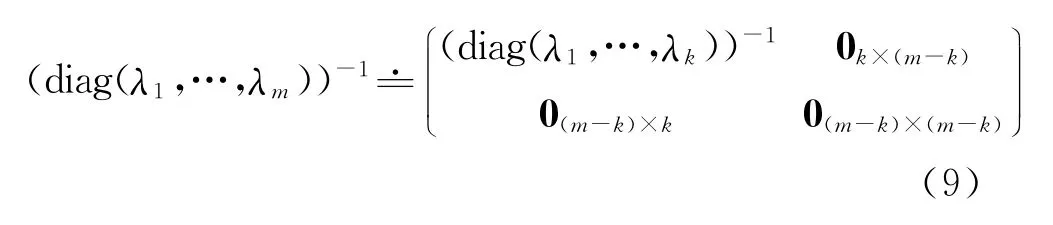
式中：下标（m－k）×k表示m－k行k列。将式（9）带入式（8），即主成分估计结果。一般情况下工程上会选取λ＞0.01作为评判是否为主成分的标准，但这种标准不具备普适性，故此该方法无法避免引入主观因素。

2 基于稀疏约束的自适应正则化模型

2.1 正则化模型及参数的选择

通过大量的地面实验可以发现，制导工具误差系数C的大部分元素数量级非常小，仅有个别元素的量级较大，故此可以认为C具有一定的稀疏性。则线性模型病态性可通过正则化的方法加以克服。

所谓正则化方法是变病态为非病态一类方法的统称，其主要手段是通过增加约束项，用来约束解空间的范围使原问题的病态性得到克服。增加的约束项通常取决于信号蕴含的内在特征，例如：假如信号本质是平坦光滑的，则可加总变分约束；如需要信号本质是稀疏的，则可加稀疏性约束。

考虑式（3），其最小二乘解可以理解为

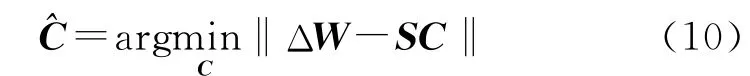
加稀疏约束的模型解可以理解为

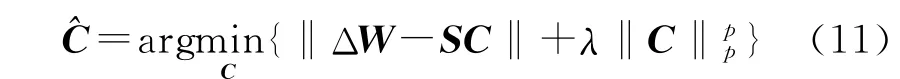
式（11）就是原问题的一般正则化模型的思想，其中λ称为正则项或者稀疏约束项，λ称为正则化参数；0＜p≤1称为正则化模型参数，简称模型参数。特殊地，当p＝0时，‖C‖0就是信号中非零元素的个数。然而由于‖·‖0是非凸的，难于求解，故此采用代替，文献［20］证明了L0约束在某些条件下与Lp约束对解的作用是等价的。

式中：s为信号C的稀疏度，可以凭经验获取，0＜p＜1。

2.2 自适应参数的正则化模型

正则化模型（10）仍然存在如何选取正则化参数λ的问题。文献［21］基于极大似然方法提供了一种可行的思路，结合本文的实际问题，经推导可以得到以下结论。

测量值ΔW（样本）的似然函数为

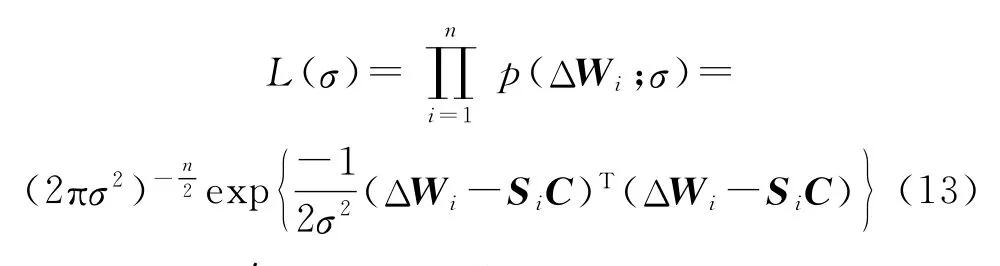
式中：σ为e′的均方误差。取式（13）的对数似然函数：

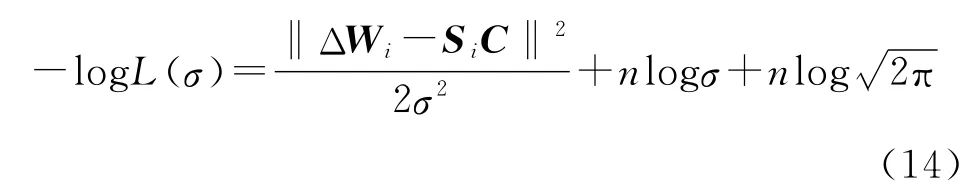
求其极小值，即为原来的极大似然函数的极大值，舍弃常数项为

注意式（15），当σ≡1时，有

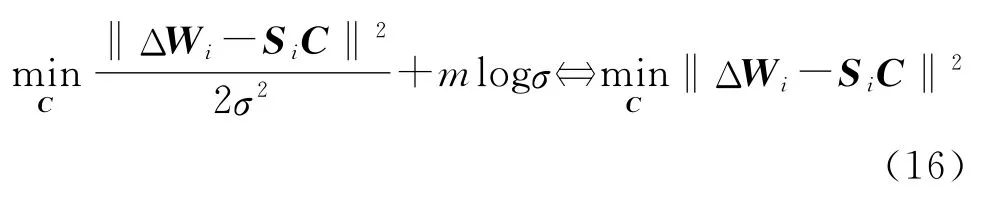
用式（16）代替逼近项模型，则可以得到新的模型：

令λ′＝λ2σ2，又由于σ2对于C的估计影响很小，将所有采样点写在一起，则模型可以简化为

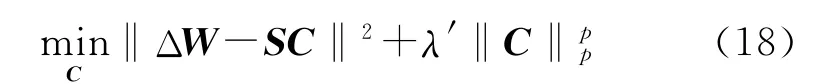
观察式（18）可知，原来的正则化参数λ已被λ′取代，其中σ2是模型噪声的方差，在迭代过程中用近似计算。其中n为对测量数据的采样数。故此，参数λ′随着逼近项的变小而变小，而λ′变小则意味着正则项的作用在不断地变弱。特别地，当→0时，正则参数λ′→0，即不需要正则项的作用。式（17）就是制导工具误差分离的自适应正则化模型。

2.3 自适应正则化模型的求解算法

针对模型（18），给出具体算法流程如下：

①取p＝arg｛＝s｝，按照经验公式选p取λ＝／s，令λ（0）＝λ；

③计算H（C（n））＝Δ2STS＋λ（n）Λ（C（n））；

④计算＝［H（）］－12STΔW，计算λ′n

3 仿真实验及结果分析

3.1 确定模型的试验结果

所谓“确定模型”，指构造模型的环境函数自变量项数是固定的。本小节以n0＝55为例分析噪声大小对于分离结果的影响，n0为模型项数。首先仿真遥外差，取e′～N（0，0.02I3），利用ΔW＝SC＋e′仿真遥外差。根据前文介绍的方法，测试以下8种算法的性能：无规范化＋最小二乘；有规范化＋最小二乘；无规范化＋主成分；有规范化＋主成分；无规范化＋正则化；有规范化＋正则化；无规范化＋自适应正则化；有规范化＋自适应正则化。计算100次，记录未超差项数n1以及3个方向的拟合残差均方差，结果如表1所示。

表1 100次实验平均结果

表中，“未超差”表示制导工具误差系数的估计值未超过真实值的±3σ范围。从表1的结果可以得到如下结论：

①从有无规范化的最小二乘计算结果可以看出，单纯的规范化不能解决矩阵病态问题。必须配合后3种方法使用；

②未经规范化的情况下，主成分分析与普通最小二乘效果相当，也就是说主成分分析应用于未规范化的数据，提高估计精度效果不显著；

③不管有无规范化操作，主成分、正则化和自适应正则化3种方法在弹道3个方向的拟合残差均方差几乎与仿真噪声的均方差一致，即解算曲线与真实曲线能够较好地吻合。

3.2 模型噪声对分离结果的敏感性分析

模型噪声对分离结果的敏感性分析是在n0＝55条件下进行的。当仿真白噪声e′的均方差取0.000 1，0.000 3，0.000 9，0.002 4，0.006 7，0.018 3的情况下，对主成分、正则化和自适应正则化方法进行100次计算，统计计算结果如图1所示。

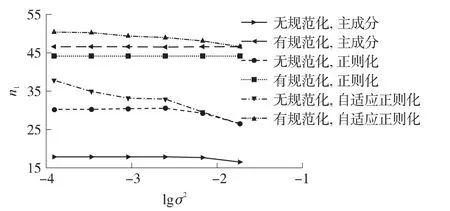
图1 不同噪声幅度下未超差项的结果比较

根据以上的实验结果可以得到如下结论：

①由图1可知，规范化能够提高估计精度。经规范化后，主成分分析方法的估计精度得到大幅度提高，其主要原因是规范化使主成分项数有所降低，未规范化时主成分有50项，规范化后主成分只有19项；

②经规范化后，自适应正则化方法的精度略高于主成分方法，主成分分析方法的估计精度又略高于需要指定参数的正则化方法的估计精度。另外，自适应参数正则化方法不需要凭借经验给定参数，且在估计效果上优于确定参数的正则化方法；

③由图1可知，随着噪声幅度的增大，所有方法得到的未超差项数都有所降低，规范化后的数据对于噪声变化相对而言不敏感，未经规范化的数据对于噪声变化较为敏感。

3.3 模型项数对分离结果的敏感性分析

本小节依次采用n0＝28，36，42，48，52，55项自变量构造环境函数矩阵，在噪声水平为0.018 3的条件下，对每种算法进行100次计算，测试各个算法对模型项数的敏感程度。结果显示，各算法平均残差都与噪声水平相当，如果以未超差项数占模型总项数的比例和超差项数为评价指标，统计结果如图2、图3所示。

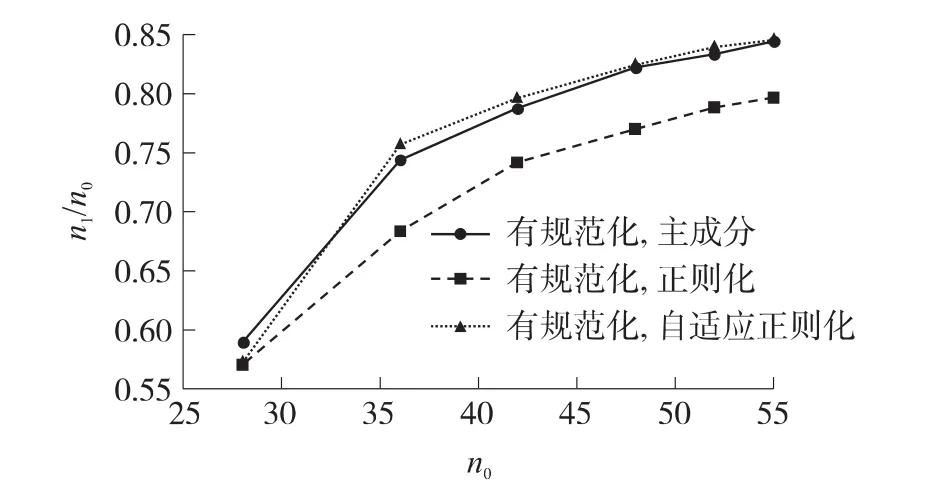
图2 n1／n0与n0的关系

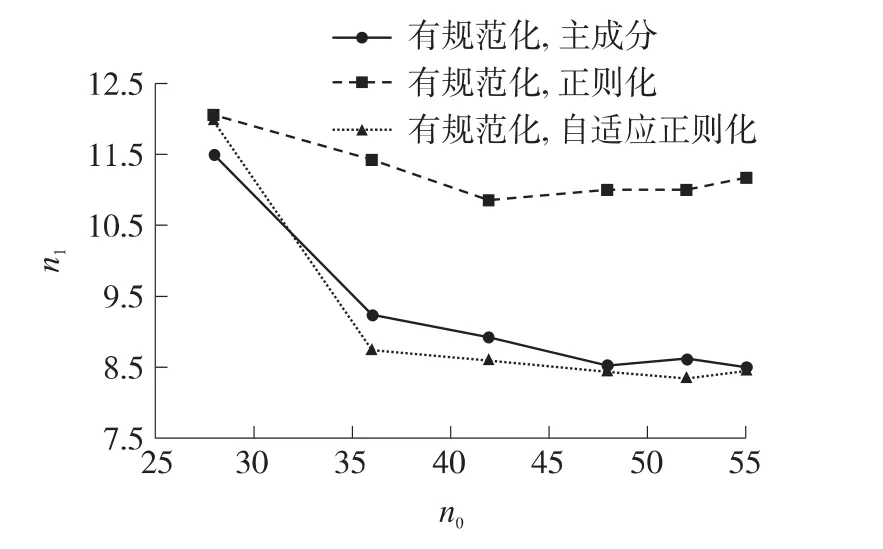
图3 n1与n0的关系

图2 显示的是平均未超差项数占模型总项数的比例随模型项数的变化，图3显示的是平均超差项数随模型总项数的变化。由以上结果可以得到以下结论：

①随着模型项数的增加，分离结果中未超差项数所占的百分比也逐步增加；

②当模型的项数大于45项时，超差项数趋于平缓；

③自适应正则化方法优于主成分方法和固定参数的正则化方法。

4 结论

本文针对制导工具误差分离线性模型，丰富和发展了基于稀疏约束的正则化模型的制导工具误差分离方法。在Bayes理论的框架下提出了自适应参数的正则化模型，避免了选取普适性正则化参数的困难，同时给出了求解算法。计算结果表明在拟合误差基本相当的情况下，从未超差项数量方面而言，自适应参数正则化模型方法优于主成分方法和指定参数的正则化方法。

［1］张最良.关于惯性制导工具误差分析的一个注记［J］.长沙：国防科技大学学报，1981，4（4）：83－88.ZHANG Zui－liang.A notation on the analysis of the error in inertial guidance tools［J］.Changsha：Journal of National University of Defense Technology，1981，4（4）：83 － 88.（in Chinese）

［2］贾沛然.用特殊弹道分离制导工具误差系数并推算正常弹道的制导工具误差［J］.长沙：国防科技大学学报，1985，8（2）：59－66.JIA Pei－ran.Use special trajectory error coefficient of guidance tool and deduce guidance tool error of normal trajectory［J］.Changsha：Journal of National University of Defense Technology，1985，8（2）：59－66.（in Chinese）

［3］沙钰，吴翊，王正明.主成分估计的发展和完善及其在制导工具误差分离中的应用［J］.航天控制，1991（S1）：136－146.SHA Yu，WU Yi，WANG Zheng－ming.Development and improvement of principal components estimation and its application in the separation of guidance instrumental tool errors［J］.Aerospace Control，1991（S1）：136－146.（in Chinese）

［4］程光显.数据的合理性检验与误差分离方法的选择［J］.航天控制，1991（S1）：104－111.CHENG Guang－xian.Selection of data reasonableness check and error separation methods ［J ］.Aerospace Control，1991（S1）：104－111.（in Chinese）

［5］徐爱平.速率捷联制导系统工具误差分析方法［J］.航天控制，1992，2（2）：34－39.XU Ai－ping.An instrumental error analysis method for strapdown guidance system［J］.Aerospace Control，1992，2（2）：34－39.（in Chinese）

［6］赵民.制导工具误差的折合方法研究［J］.导弹与航天运载技术，1993，1（1）：42－48.ZHAO Min.Conversion method of guidance instrumental error［J］.Missile and Space Vehicles，1993，1（1）：42－48.（in Chinese）

［7］罗建书，吴翊.利用假设检验评价回归系数估值精度［J］.导弹与航天运载技术，1994，2（1）：23－29.LUO Jian－shu，WU Yi.The method for appraising accuracy of estimated values of regression coefficients by hypothesis test［J］.Missile and Space Vehicles，1994，2（1）：23－29.（in Chinese）

［8］王正明，易东云.弹道跟踪数据的校准与评估［M］.长沙：国防科技大学出版社，1999：328－384.WANG Zheng－ming，YI Dong－yun.The calibration and evaluation of trajectory tracking data［M］.Changsha：National University of Defence Technology Press，1999：328－ 384.（in Chinese）

［9］姚静，段晓君，周海银.海态制导工具系统误差建模与参数估计［J］.弹道学报，2005，17（1）：33－39.YAO Jing，DUAN Xiao－jun，ZHOU Hai－yin.Modeling and pa－rameters estimation of marine guidance instrumental systematic error［J］.Journal of Ballistics，2005，17（1）：33－39.（in Chinese）

［10］孙开亮，段晓君，周海银，等.基于弹道的制导工具系统误差非线性分离方法［J］.飞行器测控学报，2005，24（4）：38－42.SUN Kai－liang，DUAN Xiao－jun，ZHOU Hai－yin，et al.A nonlinear model for separating guidance instrument systematic error based on tracking trajectory data［J］.Journal of Spacecraft TT＆C Technology，2005，24（4）：38－ 42.（in Chinese）

［11］张炜，段晓君.评估制导工具误差的Bayes估计的多层先验模型研究［J］.导弹与航天运载技术，2005，13（1）：10－13.ZHANG Wei，DUAN Xiao－jun.Multilayer prior model of Bayes method for evaluation of guidance instrumentation systematic error［J］.Missile and Space Vehicles，2005，13（1）：10－13.（in Chinese）

［12］段晓君，王正明.模型的稀疏选择与参数辨识及应用［J］.宇航学报，2005，26（6）：726－731.DUAN Xiao－jun，WANG Zheng－ming.Integrated sparse model selection and parameter identification with applications［J］.Journal of Astronautics，2005，26（6）：726－731.（in Chinese）

［13］杨华波，张士峰，蔡洪.惯导工具误差分离与折合的支持向量机方法［J］.系统仿真学报，2007，19（10）：2 177－2 179，2 182.YANG Hua－bo，ZHANG Shi－feng，CAI Hong.Separation and conversion for guidance instrumentation systematic error using support vector machines regression［J］.Journal of System Simulation，2007，19（10）：2 177－2 179，2 182.（in Chinese）

［14］杨华波，张士峰，蔡洪.基于最优LS－SVM的制导工具误差分离与折合［J］.系统工程与电子技术，2008，30（7）：1 308－1 311.YANG Hua－bo，ZHANG Shi－feng，CAI Hong.Separation and conversion for guidance instrumentation error using optimal least squares support vector machines［J］.Systems Engineering and Electronics，2008，30（7）：1 308－1 311.（in Chinese）

［15］夏青，杨华波，张士峰，等.基于遗传算法的工具误差分离与弹道折合［J］.系统仿真学报，2007，19（18）：4 130－4 133.XIA Qing，YANG Hua－bo，ZHANG Shi－feng，et al.Instrumentation errors separation and trajectory conversion based on genetic algorithm－principal component［J］.Journal of System Simulation，2007，19（18）：4 130－4 133.（in Chinese）

［16］杨华波，张士峰，夏青.弹道折合的遗传主成分方法［J］.飞行器测控学报，2007，26（6）：54－58.YANG Hua－bo，ZHANG Shi－feng，XIA Qing.A revised genetic principal components analysis for guidance instrumentation systematic error［J］.Journal of Spacecraft TT＆C Technology，2007，26（6）：54－58.（in Chinese）

［17］贺杰，黄显林，朱庆华.特征根估计方法在SINS制导工具误差估计中的应用［J］.中国惯性技术学报，2007，15（3）：282－285.HE Jie，HUANG Xian－lin，ZHU Qing－hua.Application of improved latent regression to SINS guidance instrument error estimation ［J］.Journal of Chinese Inertial Technology，2007，15（3）：282－285.（in Chinese）

［18］贺杰.SINS制导工具误差补偿研究［D］.哈尔滨：哈尔滨工业大学，2008.HE Jie.SINS guidance instrument error compensation［D］.Harbin：Harbin Institute of Technology，2008.（in Chinese）

［19］DAVID L D.Sparse components of images and optimal atomic decomposition ［R］.Stanford：Technical Report of Stanford University，2000.

［20］CETIN M，MALIOUTOV D M，WILLSKY A S.A variational technique for source localization based on a sparse signal reconstruct ion perspective［C］／／Proceedings of the 2002IEEE International Conference on Acoustics，Speech，and Signal Processing，Orlando，USA：IEEE，2002.

［21］YE Xiao－jing.Mathematical modeling and fast numerical algorithms in medical imaging applications［D］.Florida：University of Florida，2011：21－22.