聚能射流的跳弹角

李如江，蔺照东，方志坚，刘天生

（1.中北大学 安全工程系，太原030051；2.冲击环境材料技术重点试验室，山东 烟台264003）

研究人员［1－4］对穿甲弹的跳弹现象进行了大量研究，并提出了用于装甲防护设计的相应的跳弹条件。由于穿甲弹速度一般低于2 000m／s，在研究跳弹现象时一般不考虑其可压缩效应。

早在上个世纪50年代，研究人员［5］通过试验研究发现，当射流轴线与靶板表面的夹角小于一定值时射流会发生跳弹现象，即射流不能侵入靶板内部，而仅在其表面留下一条擦痕。聚能射流的头部速度一般为6 000～10 000m／s，在高速碰撞靶板过程中，由于驻点压力远远超过了弹靶材料的动态屈服强度，因而在不可压缩流体动力学理论框架内很难解释其跳弹现象。Proskuyakov［6］假定靶板材料为刚壁，考虑了射流的可压缩性，给出了射流入射靶板的跳弹条件，然而未考虑靶板的可压缩性，理论计算和试验有较大差距。

本文对已有射流跳弹条件进行了分析，在此基础上考虑了靶板材料的可压缩性，给出了射流的跳弹条件，并与试验结果进行了对比。研究结果对于装甲材料的选用和防护设计具有实际意义。

1 理论分析

1.1 靶板不可压缩条件下的射流跳弹角

Proskuyakov［6］假设平面射流在小角度条件下以超声速vj撞击靶板，将在碰撞点O产生附着冲击波，如图1所示。OS为冲击波阵面，射流材料经冲击波阵面后会改变其运动方向；另外当冲击波压力小于靶板的动态屈服强度时，靶板变形很小，可忽略不计。设射流与靶板的夹角为φ；vj2为激波后的“出流”速度；ρj，ρj2分别为射流密度和激波面后的出流密度；v1，v2分别为vj与vj2在激波面OS的切线上的投影；v′1和v′2分别为vj与vj2在激波面OS的法线上的投影；γ，φ分别为激波面OS与靶板和来流的夹角。

图1 斜入射射流的折转示意图

在激波阵面两侧，利用质量守恒和动量守恒方程以及图1中的几何关系可得出射流入射靶板的跳弹角：

式中：p为碰撞压力；η为材料的压缩率，即η＝ρj2／ρj－1。

对于密实的金属材料，冲击波作用下的p～v关系可用Hugoniot状态方程描述：

式中：cj为射流材料声速，λj为线性常数。

从式（1）可以看出，当射流密度和速度一定时，跳弹角与射流材料的压缩率有关，同时射流碰撞靶板产生的冲击波压力随材料压缩率的增加而增加。当冲击波压力大于靶板材料的动态屈服强度时，射流就会穿入靶板而不会产生反弹。对于中等硬度的靶板，其动态屈服强度约为20GPa［6］，由式（1）、式（2）即可计算出聚能射流的跳弹角与射流速度的关系。

1.2 靶板可压缩条件下的射流跳弹角

从上述射流跳弹角度计算推导过程可知，假设靶板不可压缩显然与实际不符。事实上在射流的超声速撞击下，靶板材料会在冲击波作用下产生压缩，导致射流前向运动过程中会向下折转一角度ε2，如图2所示。由于碰撞界面的向下折转，相当于射流“软着落”，导致界面压力低于不可压缩时的计算值。因此在计算射流的跳弹角时，必须对其修正。

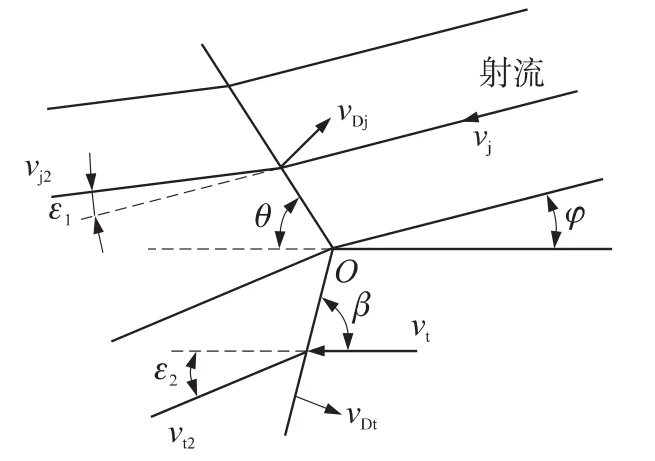
图2 斜入射射流击靶波系图

如图2所示，设vj2相对于波前来流速度vj的转角为ε1，靶中冲击波阵面后的“出流”速度为vt2，相对于来流速度vt的转角为ε2。vDj，vDt分别为射流和靶中冲击波阵面速度，激波面与靶表面的夹角为θ，靶中冲击波阵面与来流夹角为β。

在射流中激波阵面两侧利用斜激波关系可得［7］：

在靶板中激波阵面两侧利用斜激波关系可得：

式中：c为材料声速；λ为线性常数；u为质点速度；下标j，t分别表示射流和靶板相关参数，边界条件为

当已知射流和靶板材料相关参数后，利用式（3）作出pj＝pj（φ－ε1）曲线，利用式（4）作出pt＝pt（ε2）曲线，由式（5）可知，两曲线交点即为所求的解。

因此，考虑靶板的可压缩性后射流的跳弹角修正为φ′＝φ＋ε2，即

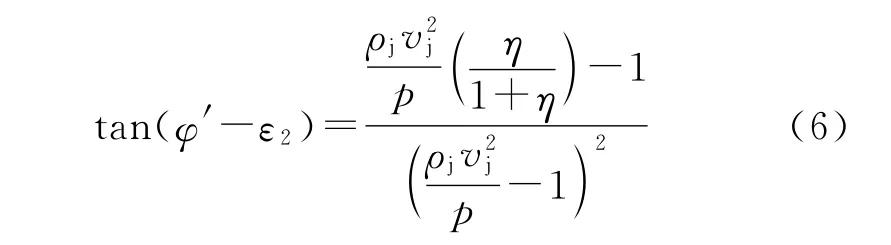
联立式（2）～式（6）可得来流速度和反弹角的关系。可以看出，射流的反弹条件不但与射流速度、密度、cj，λj和压缩率等物理参数有关，还与靶板材料的密度、ct和λt等参数相关。

2 试验研究

2.1 试验装置

采用精密聚能装药对大倾角条件下的603均质装甲钢板（RHA）进行斜侵彻试验以测定聚能射流的反弹角，精密聚能装药口径为30mm，锥角为60°，药型罩材料为紫铜，头部速度vj＝0.65cm／μs，ρj＝8.9g／cm3，声速cj＝0.396cm／μs，λj＝1.5。试验时炸高为70cm，聚能装药在此炸高条件下对603钢垂直穿深为70mm。603装甲钢相关物理参数为［7］：ρt＝7.85g／cm3，声速ct＝0.457cm／μs，λt＝1.49。试验时将聚能装药固定在20mm厚的软泡沫板上，保持聚能装药轴线水平。射流轴线与靶板表面的夹角为φ，用象限仪调整靶板角度，按1°大小顺次改变靶板的倾角，直至射流产生跳弹为止。通过观察试验现象和所测数据判断其是否跳弹。试验装置示意图见图3，现场试验见图4。

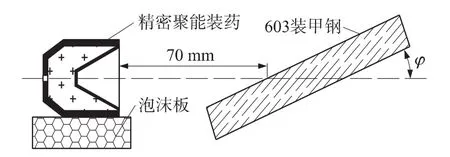
图3 试验装置示意图

图4 聚能装药侵彻试验实物照片

2.2 试验结果及分析

分别对φ＝6°，7°，8°靶板进行了侵彻试验，对斜侵彻开坑长度L、宽度B和深度H进行测量。试验结果如表1所示；试验结果照片如图5所示，其中射流从右侧侵彻。

表1 射流对不同倾角靶板的侵彻试验结果

从图5可以看出，当φ＝8°时装甲钢未被侵入，形成的开坑较大，呈椭圆形，唇缘现象很明显，射流出口处有明显崩落现象，且左侧坑壁较直，故无明显跳弹现象。当φ＝7°时，在装甲钢形成了较深的开坑，开坑入口前方有明显的喷铜现象，这可能是由于射流杵体较粗，与靶板表面作用所致，但射流并没有侵入装甲钢的内部。开坑是斜向下的，有进一步侵彻入装甲钢内部的趋势，射流出口处有崩落现象，且坑壁较直，故射流没有发生跳弹。当φ＝6°时，开坑长为100mm左右，入口处有明显的喷铜现象，其中开坑中间部位最深，向两侧依次递减，射流发生了明显的跳弹现象。

图5 φ＝6°，7°，8°时侵彻试验结果

从表1所测数据可以看出，当φ分别为8°和7°时，开坑长度、深度和宽度几乎相同，与垂直穿深相比，降低了约30%。而当φ＝6°时，擦痕长度相比7°时大了1倍，开坑深度降低了65%，而宽度与前两者相比相差不大。

图6给出了可压缩射流对刚壁斜侵彻和考虑靶板的可压缩性时的跳弹角计算结果对比，同时将文献［6］的试验结果也绘于图6中。可以看出当不考虑靶板的可压缩性时，计算结果与试验结果有较大差异，明显低于实际侵彻试验结果，而考虑靶板的可压缩性时，其预测结果与试验结果符合良好，试验结果基本落在了预测角度区间之内。射流跳弹角随其头部速度增加而减小。

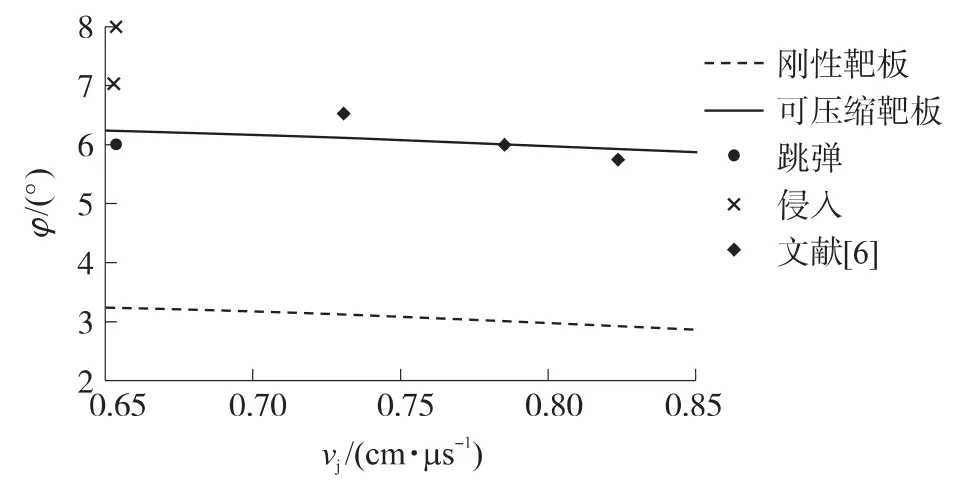
图6 计算结果和试验结果比较

3 结论

本文针对已有射流跳弹角计算方法的不足，考虑了靶板材料的可压缩性，给出了射流的跳弹角的计算方法，并与试验结果进行了对比。当射流头部以6 500m／s速度撞击603装甲钢靶，射流轴线和靶板表面夹角分别为8°和7°时，无明显跳弹现象发生；当夹角为6°时，发生了跳弹。不考虑靶板的可压缩性时，计算结果与试验结果有较大差异，明显低于实际侵彻试验结果；而考虑靶板的可压缩性时，其预测结果与试验结果符合良好。射流跳弹角随其头部速度增加而减小。研究结果对于射流的侵彻和防护设计提供了参考。

［1］SEGLETES S B.A model for rod ricochet［J］.International Journal of Impact Engineering，2006，32：1 403－1 439.

［2］SEGLETES S B.Further development of a model for rod ricochet［J］.International Journal of Impact Engineering，2007，34：899－925.

［3］DANESHJOU K，SHAHRAVI M.Penetrator strength effect in long－rod critical ricochet angle［J］.Journal of Mechanical Science and Technology，2008，22：2 076－2 089.

［4］TATE A.A simple estimate of the minimum target obliquity required for the ricochet of a high speed long rods projectile［J］.Int J Mech Sci，1977，19：661－671.

［5］张自强，赵宝荣，张锐生，等.装甲防护技术基础［M］.北京：兵器工业出版社，2000.ZHANG Zi－qiang，ZHAO Bao－rong，ZHANG Rui－sheng，et al.Basic technology of armor protection［M］.Beijing：Ordnance Industry Press，2000.（in Chinese）

［6］PROSKURYAKOV E V.Rebounding of a shaped charge jet［J］.Journal of Applied Mechanics and Technical Physics，2007，48（5）：633－635.

［7］经福谦.实验物态方程导引［M］.北京：科学出版社，1999.JIN Fu－qian.Introduction to the experimental equation of state［M］.Beijing：Science Press，1999.（in Chinese）