高超声速内外流一体化飞行器动态特性

刘 绪，赵云飞，王东方，刘 伟

（国防科学技术大学 航天与材料工程学院，长沙410073）

高超声速内外流一体化飞行器的动态稳定性参数（工程上常称为“动导数”）研究是控制系统设计和动态品质分析的重要参数，其工程需求主要体现在以下3个方面［1］：①飞行器轨道设计的重要参数；②飞行器姿态控制系统设计的重要参数；③飞行器纵、横向动态稳定性分析的重要依据。

随着美国 HyperX［2］、FALCON（猎鹰）［3］和“黑雨燕”等项目以及在欧洲、日本等项目的相继开展，吸气式高超声速飞行器的研究工作逐渐进入到工程预发展阶段［4］。内外流一体化飞行器姿态控制精度要求很高以确保进气道启动，其操稳特性分析评估也更重要，需要准确预测动导数。X－51“乘波者”高超声速飞行器第2次飞行试验，由于超燃冲压发动机的进气道未能启动而失败。HTV－2首飞试验失败，在BTT（Bank to Turn）方式实现偏航过程中飞行器沿纵轴偏转，在横滚速度达到极限后超出可控范围。美国工程审查委员会（ERB）分析认为：对飞行过程中的若干空气动力学关键参数认识有限，在缺少主动控制的条件下，HTV－2将进入弹道螺旋飞行（典型的横侧不稳定问题）。

目前国内外对动导数辨识方面的工作主要还是针对传统的以火箭发动机为动力的弹箭类飞行器，对包含内流的吸气式飞行器动态特性研究较少。因此高超声速内外流一体化飞行器的研制亟需开展动态特性模拟技术研究。其核心是三方向（俯仰／偏航／滚转）的直接阻尼导数模拟方法研究；同时还迫切需要开展加速度导数、交叉导数、交叉耦合导数的数值算法研究，为纵横向耦合运动特性研究提供技术支撑。动导数预测及稳定性预示将为飞行器控制系统设计、高超声速飞行器动不稳定发生的边界分析及相应的动态稳定性判据研究提供关键气动参数。

动导数计算方法分为小扰动线化理论、牛顿理论与气动力工程模型相结合的动导数工程近似方法、模拟动态实验的数值自由振荡法、数值强迫振荡法。工程近似方法的最大特点在于快捷，但依赖于经验性，考虑气流分离、再附和尾流等效应较为困难，对于包含内流的一体化复杂外形流动难以适应。因此考虑了流动非线性的模拟动态实验的全数值计算是动导数研究发展的重要方向。

本文在Etkin非定常气动力模型基础上，给出了小振幅强迫振动下的俯仰、偏航和滚转三方向直接阻尼导数的强迫简谐分析方法，并发展了包括交叉导数、交叉耦合导数在内的多种动导数辨识方法。在采用Finner标模验证的基础上，开展了高超声速内外流一体化飞行器的动态特性分析。

1 数值方法

在贴体坐标系ξ－η－ζ下，对完全气体、忽略质量

力下的三维无量纲Navier－Stokes方程形式如下：

式中：U为守恒变量；E，F，G为无粘通量；Ev，Fv，Gv为粘性通量。

本文在空间上采用二阶精度的Roe格式。Roe格式是基于Godunov方法的基本思路发展起来的，是通量差分分裂（FDS）格式的一种，由于其优秀的间断分辨率和较小的数值耗散性，目前得到广泛的应用。采用引入“双时间步”（dual－time－step）方法的LU－SGS隐式格式离散流体运动方程时间项。动网格生成采用刚性网格生成方法。远场入流边界采用适用于动态边界条件下的一维Riemann不变量的无反射边界条件。对于定常／非定常超音速出流，边界点上的值由内流场计算结果外推得到。对于壁面边界，采用速度无滑移、绝热壁条件。奇性轴采用外插后周向平均处理。

2 动导数计算方法

在飞行器姿态控制系统设计及轨道（弹道）设计中，所需要的动态稳定性参数有数十个之多。表1列出了一些重要的动态阻尼导数［5］。表中：Cl，Cm，Cn分别为滚转、俯仰、偏航力矩系数；α，β分别为攻角和侧滑角；p，q，r分别为滚动轴、俯仰轴、偏航轴的角速度分量。目前国内外公开文献主要是研究俯仰、偏航或滚转三方向的直接阻尼导数，而对交叉导数、交叉耦合导数的数值计算较少涉及。本文采用小振幅强迫简谐分析法给出了多种导数的数值辨识方法。

表1 动态阻尼导数

飞行器做单自由度的俯仰运动，如果其质心速度不变，则确定运动的独立状态变量只有攻角α和俯仰角速度q。对俯仰力矩系数Cm，根据Etkin假定［6］，俯仰力矩系数可写成：

给定强迫振动：α（t）＝θ＝α0＋αmsinkt，其中，α为瞬时攻角，θ为俯仰角，α0为基准状态的攻角，αm为攻角振幅，k为减缩频率。在k不很大且忽略高阶导数的影响时，当非定常振动过程达到谐振解，通过数值积分可以求出俯仰阻尼导数为

式中：ts为积分起始时间，Tc为振动周期。

类似地，通过给定不同的扰动方式可以推导出其他类型的动态稳定性参数的计算公式。其中强迫滚转运动的形式为φ＝φmsinkt，φ为滚转角，φm为滚转角振幅；强迫偏航运动的形式为ψ＝ψmsinkt，ψ为偏航角，ψm为偏航角振幅。

3 验证算例

本文采用Finner标模作为验证算例，Finner标模是外形为“十”字翼的导弹，其动态特性有标准实验数据和基于准定常欧拉方程的求解结果。图1给出了“十”字翼导弹的外形尺寸［7］。导弹全长L为10倍的弹体直径。本文采用块间完全对接的多块结构化网格，对称面网格与分区情况见图2。网格总量为200万。近壁第一层网格到壁面的距离为1×10－4L。

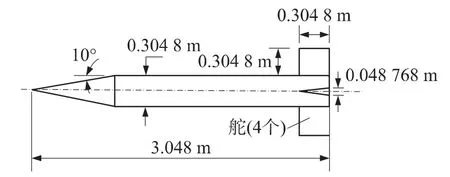
图1 “十”字翼导弹外形尺寸

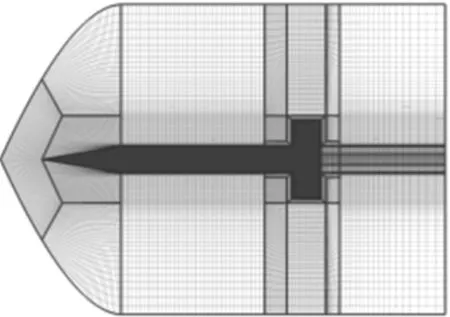
图2 对称面网格与分区图

3.1 俯仰阻尼导数辨识

给定强迫俯仰振动形式α（t）＝θ＝α0＋αmsinkt，其中初始攻角α0＝1.5°，振幅αm＝1.5°，减缩频率k＝0.05，质心位置Xcg／L＝0.5。

图3给出了俯仰阻尼导数的计算结果与实验数据［8］和基于准定常欧拉方程结果［9］的比较。从中可以看出，本文预测的俯仰阻尼导数比文献中采用准定常欧拉方程的求解结果更加接近风洞实验的数据。

图3 俯仰阻尼导数计算结果

3.2 滚转阻尼导数辨识

给定强迫滚转振动形式φ＝φmsinkt，取φm＝2.5°，k＝0.05，Xcg／L＝0.5。

图4将强迫滚转辨识出的动导数与文献［10－11］中的实验数据进行了比较。滚转阻尼导数的实验精度一般不高，主要由于实验中存在支架、洞壁干扰等不确定因素，这使对同一模型在不同风洞中的实验结果也存在一定的差异。本文计算得到的滚转阻尼导数介于2个实验结果之间，验证了方法和程序的可靠性。

图4 滚转阻尼导数计算结果

4 动态特性分析

高超声速巡航导弹X－51是美国空军研究实验室（AFRL）联合波音公司（负责机身）和普惠公司（负责发动机）研制的一架超燃冲压发动机验证机－乘波器（SED－WR）飞行试验平台。本文以内外流一体化飞行器X－51为背景，利用公开的图像数据资料进行反向建模，生成的类X－51三维实体外形见图5，其进气道内部结构见图6。通过开展小振幅强迫简谐运动的非定常流场数值模拟，对进气道冷流状态下的类X－51动态稳定性参数进行数值辨识。

图5 类X－51三维实体外形

图6 进气道内部结构

4.1 直接阻尼导数辨识

计算采用块间完全对接的多块结构化网格，网格总量为460万，共划分为62块。不同位置的结构化网格与拓扑结构见图7和图8。计算条件为：马赫数6.5，高度27km。俯仰／偏航／滚转3个方向的强迫简谐运动的振幅均为1°，k＝0.1，无量纲时间步长Δt＝0.005。图9给出了攻角为0°时的强迫俯仰振动一个周期内不同时刻的压力等值线，其中ti＝ts＋（i－1）Tc／4，i＝1，2，3，4。头部斜激波、膨胀波以及尾翼激波在图中清楚地反映出来，内部流动已经建立。同时可以看出强迫振动的振幅很小导致各时刻流场状态差别不大。在攻角0°～6°范围之间本文给出了3个方向强迫振动的力矩系数曲线，如图10～图12所示，图中，Cmm，Cml，Cmn分别为俯仰、滚转、偏航力矩系数。

图7 对称面网格与分区图

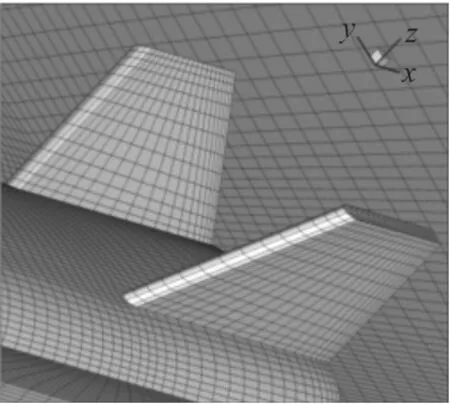
图8 舵面附近的结构化网格

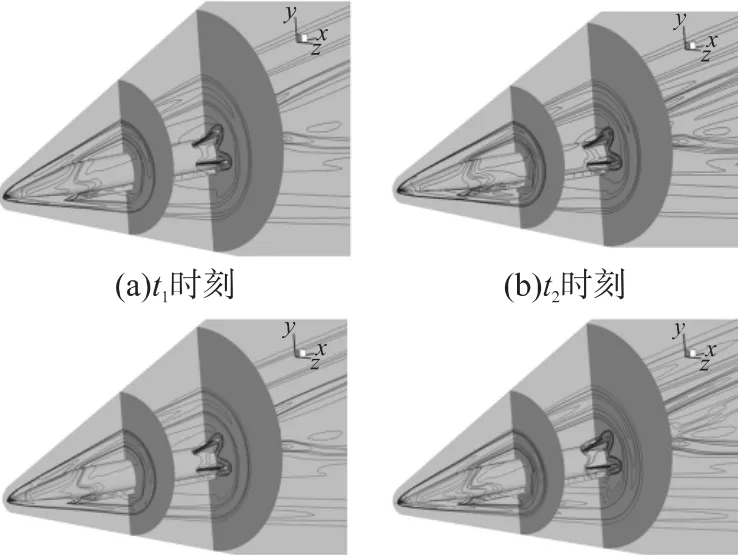
图9 一个周期内不同时刻的压力等值线

图10 （a）、图11（a）和图12（a）分别给出了俯仰、滚转和偏航运动对应力矩系数的迟滞环曲线。这是非定常运动时物体上漩涡运动和物面运动之间存在的时间延迟现象在气动力系数上的反映。迟滞环形状饱满，非定常滞后效应比较明显。在计算启动后一个振荡周期内即进入迟滞环，迟滞环重复性较好。不同攻角下的强迫振荡迟滞环的转动方式相互一致。从与3个迟滞环相对应的时间历程曲线图10（b）、图11（c）和图12（d）可以看到，非定常气动力矩收敛情况很好，从第2个周期开始已经完全达到谐振。3个振动方向上的俯仰力矩系数、滚转力矩系数、偏航力矩系数随时间按正弦规律变化。

图10 强迫俯仰振动力矩系数曲线

图11 强迫滚转振动力矩系数曲线

通过积分强迫简谐振动的迟滞环曲线，表2给出了俯仰／偏航／滚转3个方向的直接阻尼导数辨识结果。各方向下的直接阻尼导数均为负值，说明飞行器在俯仰／偏航／滚转方向受到扰动后处于动稳定状态。俯仰阻尼导数和偏航阻尼导数量级一致，但滚转阻尼导数要小1～2个量级。

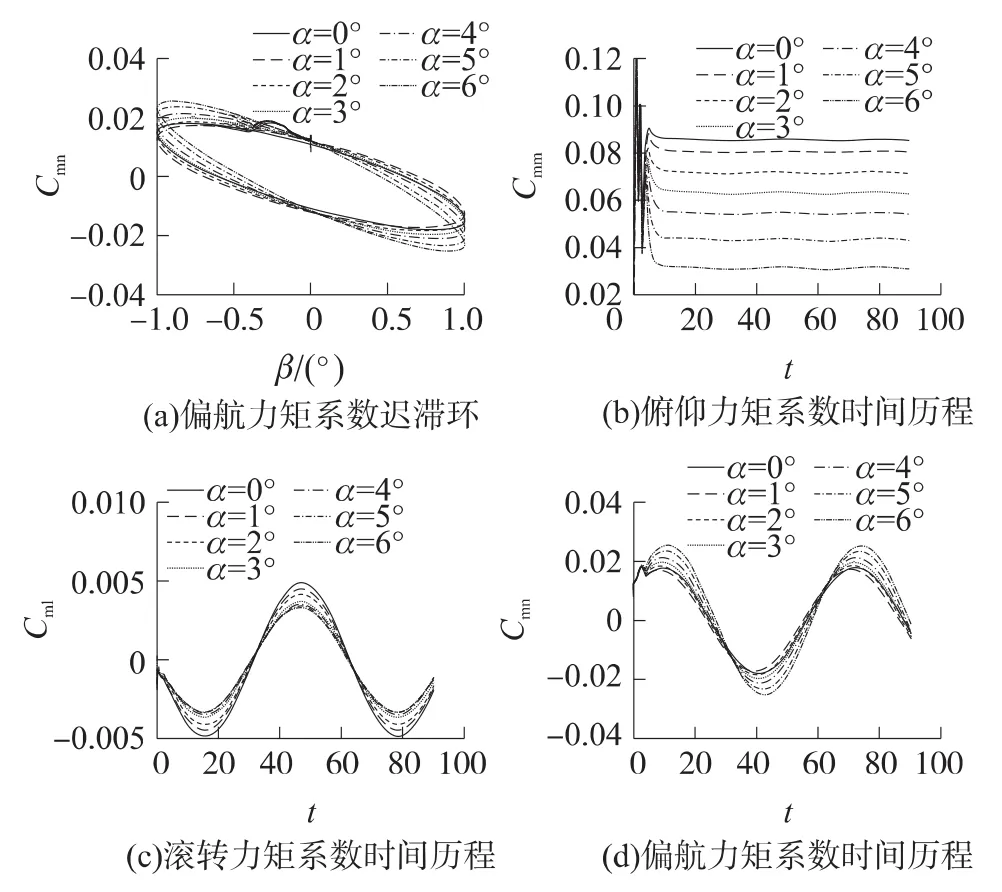
图12 强迫偏航振动力矩系数曲线

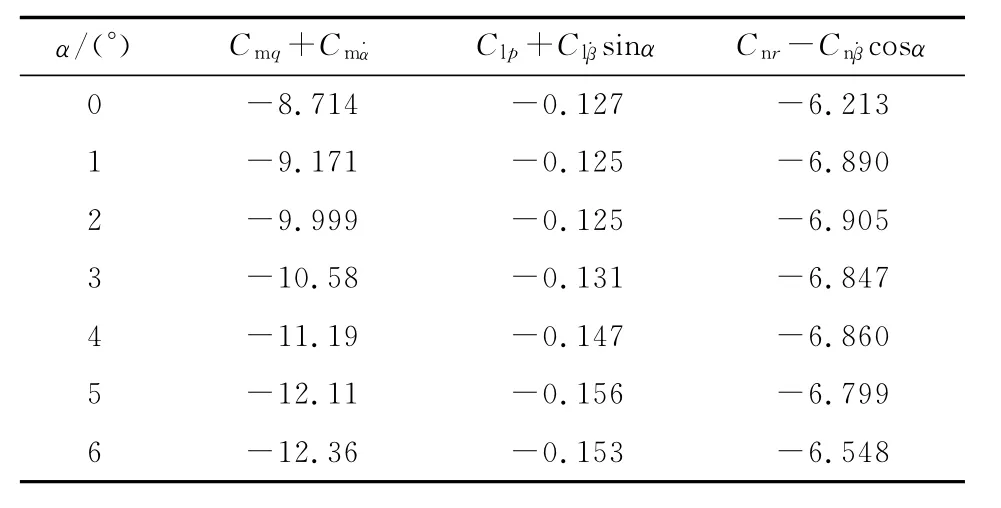
表2 直接阻尼导数辨识结果

4.2 交叉阻尼导数辨识

图11（d）和图12（c）的偏航和滚转力矩系数随时间变化能够达到谐振，周期性变化明显，说明滚转方向和偏航方向的交叉性较强。但图10（c）和图11（b）中的力矩系数基本为一个常数，受周期性简谐运动的影响不大，说明俯仰方向和滚转方向的交叉耦合性很弱。类似地，图10（d）和图12（b）显示出俯仰方向和偏航方向的交叉耦合性同样很弱。综合上述规律，在本状态下飞行器偏航与滚转横向之间的影响明显，但纵横向交叉耦合性不强，故本文对交叉导数开展了数值辨识工作，其结果列于表3。

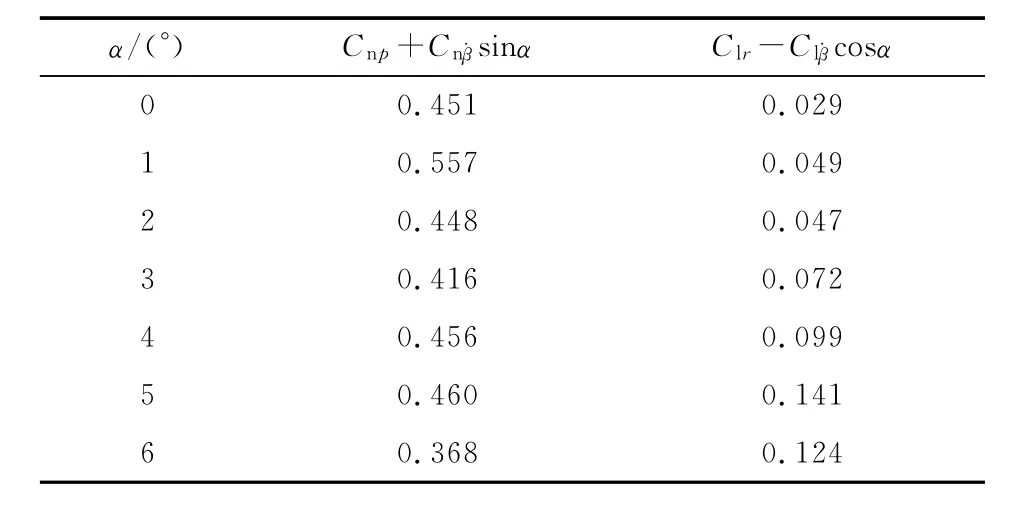
表3 交叉阻尼导数辨识结果

从辨识结果来看，强迫滚转运动时滚转阻尼导数在各计算状态下均为负值，而滚转－偏航力矩交叉导数均为正值，二者量级相差不大，说明飞行器在滚转时是动稳定的，但可能引起偏航方向的动不稳定问题，需要控制系统对其姿态进行控制。强迫偏航运动与此类似，偏航阻尼导数在各计算状态下均为负，而偏航－滚转力矩交叉导数均为正，但其量级比偏航阻尼导数小2个量级。计算时涉及表面摩阻等复杂的计算问题，增加了计算难度，因此交叉导数的计算还需做深入研究。

4.3 强迫振荡计算参数选取比较

强迫振动法辨识动态稳定性参数的精度依赖于3个重要的计算参数：时间步长、子迭代步数、减缩频率。时间步长和子迭代步数这2个参数的组合实际上决定了双时间步方法计算非定常流动的收敛程度。频率相似问题是影响强迫振动法辨识动导数精度的重要影响因素。本文选取了几组不同的参数值，分别考察时间步长、子迭代步数、减缩频率对包含内流的高超声速飞行器动导数辨识的影响。

减小时间步长、加大子迭代步数都可以提高非定常流动的收敛程度，从而提高动态稳定性参数的辨识精度，但计算量也会大幅增加。因此有必要先进行强迫振荡的试算，确定保证准确度的适宜计算时间步长和子迭代步数。本文无量纲时间步长Δt取0.005，子迭代步数n为5步，在保证计算精度的前提下有较好的计算效率。表4给出了更小的时间步长和更大的子迭代步数时的动导数辨识结果，可以看到计算结果基本一致。

表4 不同时间步长和子迭代步数下的动导数辨识结果

减缩频率实际上是强迫振动频率快慢的反映，其大小会影响动导数的量值乃至符号。减缩频率的选取必须像马赫数、攻角一样考虑到与实验的相似性。本文以强迫滚转运动为例，考察了不同减缩频率对动导数辨识的影响。图13显示出迟滞环随减缩频率增加由内而外形成嵌套。减缩频率越小，迟滞环曲线越狭长，非定常滞后效应越弱，动导数辨识难度高，非定常流场的计算量增大。但考虑到与实际情况的相似性，k不应取得过大，否则影响计算精度。表5给出了不同k值的滚转阻尼导数和滚转－偏航交叉导数，可以看出减缩频率对动导数辨识结果的影响，随着k的增大，横向之间的影响加强。

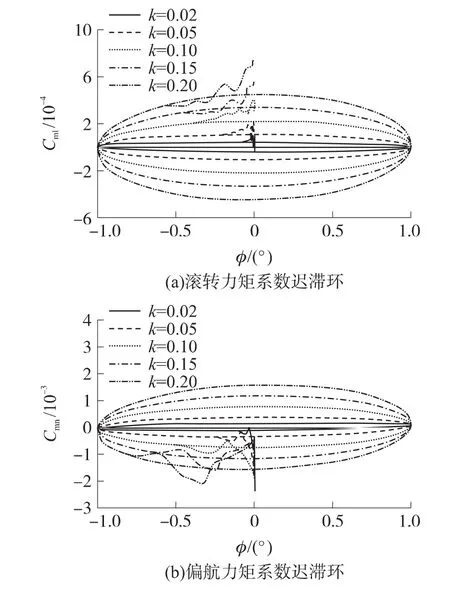
图13 强迫滚转振动不同减缩频率下的迟滞环曲线

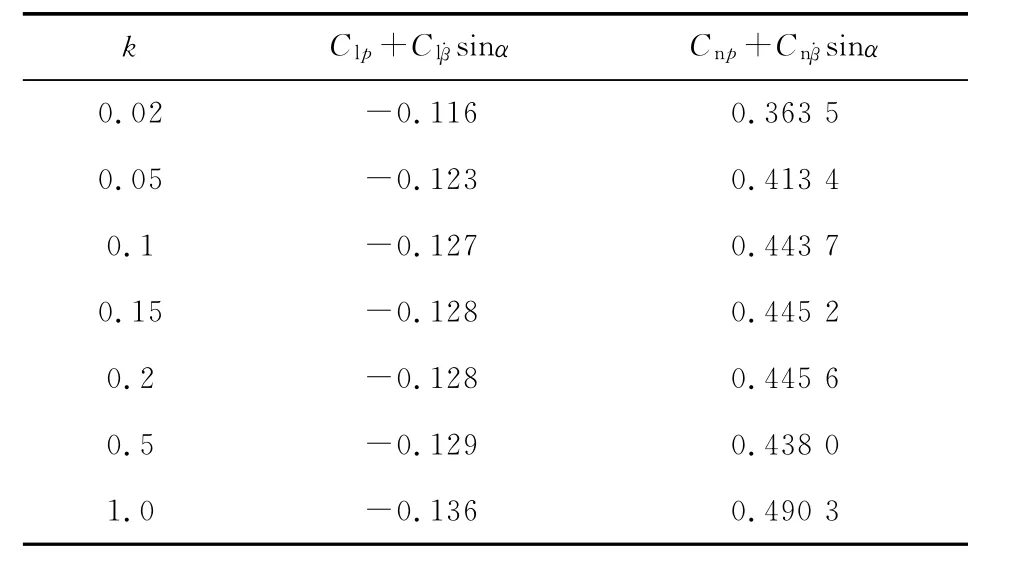
表5 不同减缩频率下的动导数辨识结果

5 结论

本文基于三维非定常N－S方程，采用小振幅强迫简谐分析法开展了高超声速内外流一体化飞行器动态气动参数的计算研究。本文给出的动导数辨识技术不仅适用于传统的以火箭发动机为动力的弹箭类飞行器，对包含内流的吸气式高超声速飞行器适用性良好，各攻角下的非定常滞后效应明显，迟滞环重复性较强。辨识得到的高超声速飞行器3个方向的直接阻尼导数均为负值。对横侧向动稳定性、纵横向耦合动稳定性问题的分析显示，其纵横向耦合性不强，但横向之间的交叉影响明显，各交叉导数均为正值，但可能引起偏航／滚转方向的动不稳定问题，需要控制系统对其姿态进行控制。

［1］刘伟.细长机翼摇滚机理的非线性动力学分析及数值模拟方法研究［D］.长沙：国防科学技术大学，2004.LIU Wei.Nonlinear dynamics analysis for mechanism of slender wing rock and study of numerical simulation method［D］.Changsha：National University of Defense Technology，2004.（in Chinese）

［2］PEEBLES C.The X－43Aflight research program：lessons learned on the road to Mach 10［M］.Washington，D.C.：AIAA Inc.，2007.

［3］WALKER S，RODGERS F.Falcon hypersonic technology overview，AIAA－2005－3253［R］.2005.

［4］杨超，许赟，谢长川.高超声速飞行器气动弹性力学研究综述［J］.航空学报，2010，31（1）：1－11.YANG Chao，XU Yun，XIE Chang－chuan.Review of studies on aeroelasticity of hypersonic vehicles［J］.Acta Aeronautica et Astronautica Sinica，2010，31（1）：1－11.（in Chinese）

［5］童秉纲，陈强.关于非定常空气动力学［J］.力学进展，1983，13（4）：377－394.TONG Bing－gang，CHEN Qiang.Some remarks on unsteady aerodynamics［J］.Advances in Mechanics，1983，13（4）：377－394.（in Chinese）

［6］刘伟，杨小亮，赵云飞.高超声速飞行器加速度导数数值模拟［J］.空气动力学学报，2010，28（4）：426－429.LIU Wei，YANG Xiao－liang，ZHAO Yun－fei.Numerical simulation of acceleration derivative of hypersonic aircraft［J］.Acta Aerodynamica Sinica，2010，28（4）：426－429.（in Chinese）

［7］MIKHAIL A G.Roll damping for projectiles including wraparound，offset，and arbitrary number of fins［J］.Journal of Spacecraft and Rockets，1995，32（6）：929－937.

［8］SHANTZ I，GROVES R T.Dynamic and static stability measurements of the basic finner at supersonic speeds，NAVORD Report 4516［R］.1960.

［9］OKTAY E.CFD predictions of dynamic derivatives for missiles，AIAA 2002－0276［R］.2002.

［10］REGAN F J.Roll damping moment measurements for the basic finner at subsonic and supersonic speeds，NAVORD Report 6652［R］.1964.

［11］WHYTE R H.Spinner－a computer program for predicting the aerodynamic coefficients of spin stabilized projectiles，Genera1 Electric Class 2Reports［R］.1969.