一种改进的自适应滑模变结构导引律

高 峰，唐胜景，师 娇，郭 杰

（1.北京理工大学 宇航学院飞行器动力学与控制教育部重点实验室，北京100081；2.中国运载火箭技术研究院，北京100076）

现代战场立体化的趋势对武器系统多用途化的需求逐步提高。对于新一代反坦克导弹，不仅要求能够摧毁地面装甲目标，还要求其具备一定的低空防御能力，如打击处于攻击状态的武装直升机。

相比于主战坦克、装甲车等地面目标，空中目标的机动性更强；但另一方面，由于飞行的需要，空中目标的防护相对薄弱，只要命中目标，反坦克导弹常用的战斗部足以对目标造成致命毁伤。一般反坦克导弹的飞行速度与可用过载均低于专用的防空导弹，因此需要根据导弹的具体情况，设计合适的导引律，使其在保证命中精度的同时能够合理分配弹道的过载。

经典比例导引律是攻击非机动目标的最优导引律，可以实现非机动目标视线角速度的零化，但在攻击机动目标时其性能会急剧下降。为提高导弹对高机动目标的拦截能力，研究人员基于不同的出发点提出了一些高精度改进比例导引律［1－3］，虽然可以实现对机动目标的攻击，但存在着所需导引信息过多，或者形式复杂等问题，且并不适用于速度较低的反坦克导弹。

滑模变结构控制对干扰和摄动具有某种完全自适应的优点［4］，而且滑动模态对摄动的不变性十分有益于控制系统的设计。另外，滑模变结构控制设计比较简单，便于理解应用，因此在导引律尤其是拦截高机动目标导引律的研究中得到了广泛的应用与发展［5－10］。

本文以零化弹目视线角速度为出发点，设计了一种自适应滑模变结构导引律，并根据实际研究中出现的具体问题，改进了变开关项的形式，并综合应用饱和函数，削弱了变结构控制的抖振现象，最终形成一种改进自适应滑模变结构导引律。导引律可以满足反坦克导弹对空中目标的命中精度需求，同时可以合理分配末制导段的法向过载。

1 弹目相对运动关系

在纵向平面内，导弹与目标的相对运动关系示意图如图1所示。图中，r为导弹相对目标的距离，vM为导弹速度，θM为导弹弹道倾角，q为弹目视线角，vT为目标速度，θT为目标航迹角。规定水平基准线逆时针旋转到弹目视线上时，q为正，反之为负。

根据图1所示的运动关系，得到弹目相对运动关系方程组：

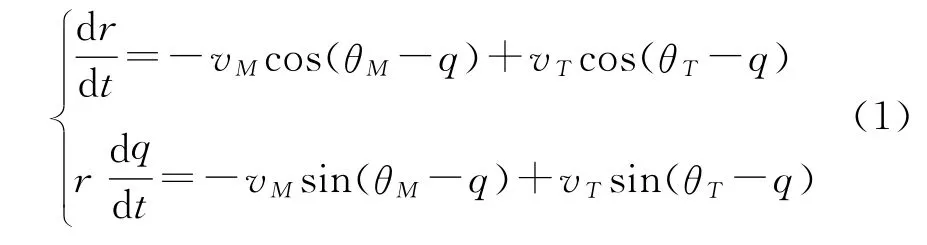
2 导引律初步设计与分析

2.1 导引律推导

对式（1）第二式求微分，并根据第一式进行简化，可得：

取u＝为控制项，由式（2）可得：

在导引律的设计中，根据准平行接近原理，一般希望在制导过程中使视线角速度趋近于0，即使导弹在目标机动时也可以实现的零化。为达到这个目的，应用滑模变结构理论，选取＝0作为导引律的切换平面，即切换函数设计为

通过变结构控制，使系统在有限时间内到达切换平面内，系统进入滑动模态时，即可使在有限时间内零化，满足＝0的理想导引要求，在滑动模态附近，渐进实现平行接近导引。

为使系统到达切换面，要求系统的运动必须趋向切换平面，即满足可达性条件：

可达性条件保证了系统运动可以在有限时间内到达切换平面，但对这段时间内具体的状态轨迹没有约束。为改善这段运动的动态品质，可以通过趋近率的设计加以控制。在滑模变结构导引律的研究中，常采用指数趋近率的形式。根据导弹控制系统的时变性，设计一种对时变参数具有自适应能力的指数趋近率，具体形式为

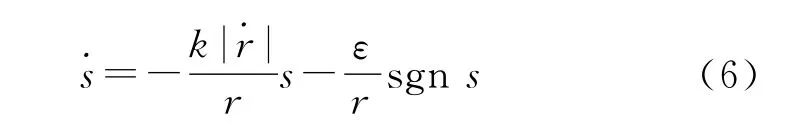
式中：k＞0，ε＞0。

趋近率表达式（6）的自适应性主要体现在切换函数向切换面的运动速率随弹目距离r的变化而调整。在末制导初始阶段，r较大，趋近速率较慢；随着导弹接近目标，r→0时，趋近速率迅速上升，保证了不会发散，从而提高了命中精度。在式中，当s＝→0时，趋近速率约等于ε／r，可以保证有限时间到达切换面。由于趋近率的自适应性，最终得到的导引律也具有了自适应能力。

将式（4）、式（6）代入式（3），求得控制项：

在实际制导过程中，目标的机动信息一般很难准确获取，通常利用卡尔曼滤波或扩展卡尔曼滤波技术，通过建立目标机动模型，可以实现目标的加速度估计。但这种假设的目标机动模型在工程上可能存在很大的建模误差，甚至导致糟糕的估计结果。因此，在滑模变结构导引律的研究中，可以将其作为干扰项处理［11］。

将d作为干扰项进行简化后，式（7）可简化为

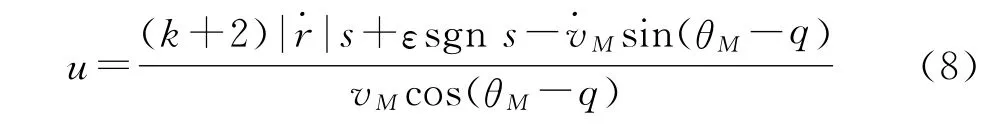
从而可以得到自适应滑模变结构导引律的形式：

2.2 稳定性分析

构造Lyapunov函数：

根据式（3）以及式（8），可得Lyapunov函数的导数：

式中：d′为目标机动干扰项的预估值，可根据目标特性离线估计。

根据Lyapunov稳定定理，为使导引律收敛，需要有＜0。因此，根据式（11），需要满足：

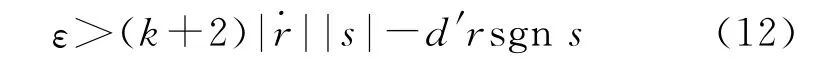
则可保证系统渐进稳定。

2.3 导引律分析

如式（9）所示，设计的自适应滑模变结构导引律可视为由比例导引项、切换偏置项以及加速度补偿项等3部分组成。反坦克导弹在末制导段一般进行无动力飞行，切向加速度较小，若忽略导弹攻击段的切向加速度，则式（9）可简化为

即导引律可视为一种具有时变比例系数和一个切换偏置项的改进比例导引律。该导引律无需估计目标机动信息，仅需目标机动的界限即可。滑模条件满足时，控制指令中的切换偏置项起到了估计目标加速度的作用。

3 导引律的改进

3.1 抖振的削弱

对于采用滑模变结构控制的系统，在实际控制过程中，开关在时间和空间上的滞后会导致控制的不连续性，产生抖振现象，进而影响控制系统的稳定性，导致导弹命中精度的降低。抖振是变结构控制系统的严重缺陷，也是阻碍变结构控制应用的主要障碍［12］。在导引律的研究中，为削弱抖振现象的影响，目前最常用的方法是饱和函数法，另外还有变开关项系数法等。

1）饱和函数法。

饱和函数法的基本思想是将不连续的符号函数连续化，具体可将符号函数取代为

或

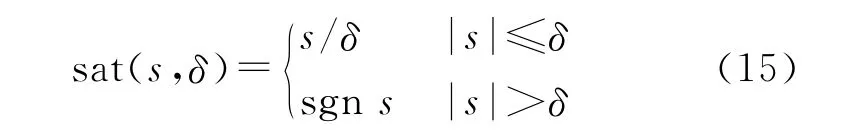
式中：δ＞0，是一个微小量，一般可称为边界层厚度，也称为消颤因子［13］。

以改进后的函数代替符号函数，可使控制在切换面附近具有高增益性。若δ较小，则可保持高度的鲁棒性；但实际在控制器上，大幅时间滞后需要较大的δ，且在极端情况下，将导致大幅振动且系统不再是变结构系统。

在饱和函数法的2种形式中，式（14）抑制抖振的效果更好，因此也更为常用。另外还有一种死区法，可视作饱和函数法的一种变形，因其抑制抖振的效果不如饱和函数法，所以并不常用。

2）变开关项系数法。

变开关项系数法可以视作趋近率参数调节方式的一种改进，趋近率表达式中含有符号函数的εsgn称为开关项，系数ε的取值非常关键。根据式（6），若ε选择较小的值，状态轨迹接近切换面时的运动速率变小，可有效减小颤振幅度。但若ε选择过小，会导致到达切换面的时间无穷大，系统不再是滑动模态控制系统。

因此，为兼顾减少到达切换面的时间以及控制抖振幅度的目的，可设定ε为变量，随着接近切换面，使ε逐渐减小。在文献［14］中，刘永善等人研究了基于模糊控制技术确定ε变化的形式，可有效削弱抖振。但该方法需要应用弹上传感器等设备对目标的运动进行预估，并且模糊器的设计也为导引律的设计增加了难度。

为此，本文采用变开关项系数法时，对ε的形式进行了改进，将ε设计为随r逐渐减小的变量，即随着导弹飞向目标，ε也随之减小。为简单起见，ε的形式设计为r的一次函数，即

式中：a＞0，b＞0，其取值需要根据ε的取值范围及r的变化范围进行。在接近目标时，r逐渐接近于零，因此可首先确定b的取值，其作用是保证系统在末制导的大部分时间内处于滑模控制系统；然后根据末制导开始时r的最大值和ε的上限进行a的取值，在保证系统可以较快进入滑模面的同时尽量减小抖振幅度。根据趋近率表达式中ε的作用可知，a和b的取值越大，系统进入滑模面的速度越快，同时出现抖振的可能性或抖振幅度也会增大。

3.2 导引律的改进

研究中发现，分别采用饱和函数或变开关项系数进行抖振的削弱处理，难以有效地削弱抖振现象。

如图2～图3所示，分别采用饱和函数法和变开关项系数法时，虽然末制导段的弹目视线角速度进入滑模面的速度较快，但均出现了不同程度的抖振现象。其中，采用变开关项系数法时，尽管对的抑制效果更好，但抖振现象也更为严重。而且饱和函数中消颤因子δ取值越小，或是变开关项系数中参数a和b的取值越大，抖振现象越严重；反之，对的抑制效果会下降，当抖振现象完全消除时，甚至无法进入滑模面。

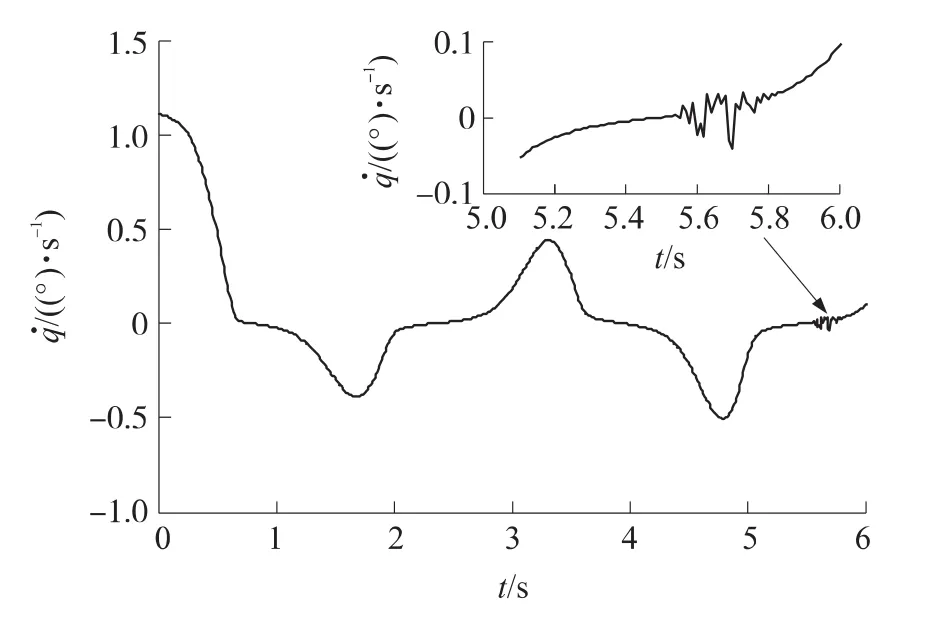
图2 采用饱和函数法时的弹目视线角速度曲线

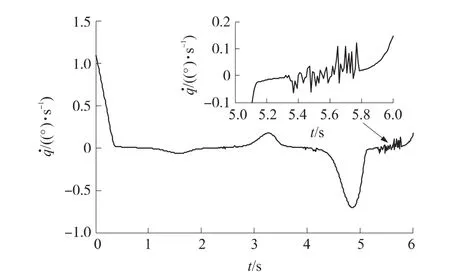
图3 采用变开关项系数法时的弹目视线角速度曲线

图4 采用饱和函数法时的法向过载曲线

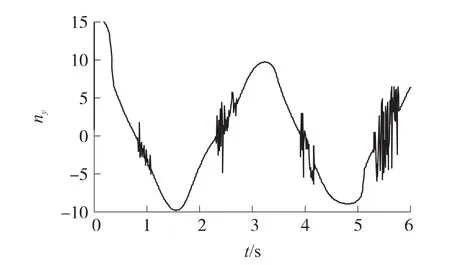
图5 采用变开关项系数法时的法向过载曲线

在本文研究中，尝试综合采用饱和函数法和变开关项系数法进行消颤处理，取得了较好的效果。首先，用饱和函数替换导引律表达式中的符号函数，然后采用本文设计的一次函数形式的变开关项系数，将式（14）和式（16）代入式（9），最终得到改进的自适应滑模变结构导引律：

若忽略导弹攻击段加速度，则式（17）可变为

4 仿真分析

基于导引弹道仿真对设计的导引律进行仿真分析，仿真参数设置如下：导弹平飞高度h＝150m，速度为vM＝180m／s；目标初始位置（2 000，300）（m）；转入末制导时刻弹目水平距离rx＝1 000m，并以此时刻作为仿真开始时间，即t＝0；同一时刻目标开始作蛇形机动，目标运动参数为vT＝50m／s＝10g（cos2t）／vTs－1；导引头盲区距离为70 m，导弹进入盲区时给予视线角速度信号零值，以此为依据计算脱靶量。仿真中比例导引律（PNG）的比例系数取4；改进自适应滑模变结构导引律（IAVSG）中的参数取值为k＝2，δ＝0.001，a＝0.1，b＝50。仿真得到弹道曲线以及各类参数变化曲线如图6～图9所示。

图6 弹道曲线比较

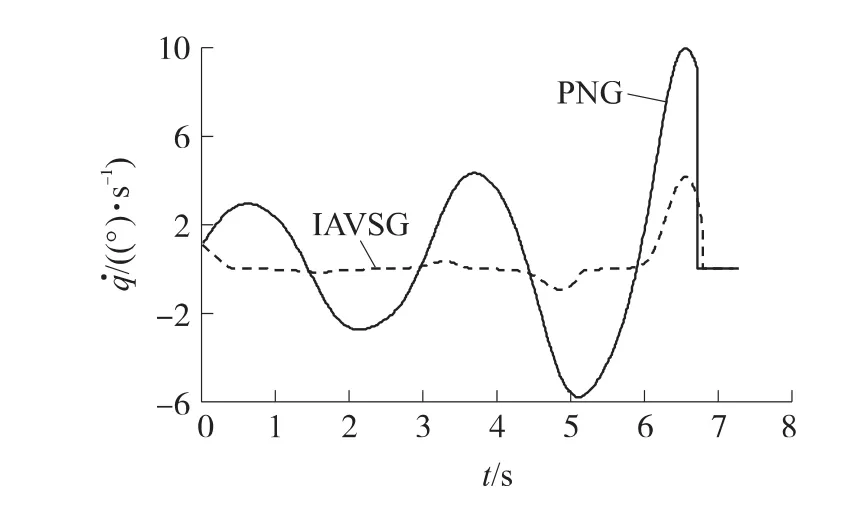
图7 弹目视线角速度曲线比较

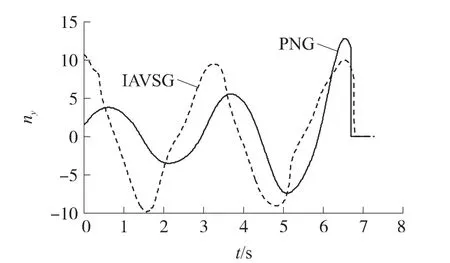
图8 法向过载曲线比较

图9 弹目视线角曲线比较

如图6所示，IAVSG的弹道曲线机动幅度比PNG大，而且距目标越远时这种对比越明显，说明IAVSG为抑制的变化在末制导开始阶段导弹就需要随目标的机动进行较大幅度的机动。

如图7所示，在末制导开始后，采用IAVSG的很快进入滑模面，在最后阶段由于弹目距离过小才离开了滑模面。与图2、图3相比，进入滑模面的速度较快，虽然对的抑制效果稍差，却完全消除了的抖振现象。而采用PNG时变化很大，尤其在接近目标时甚至接近10（°）／s。

抑制的代价就是在追击过程中一直需要导弹进行较大幅度的机动，因此法向过载会保持在较大的范围内变化，如图8所示。但在接近目标时，IAVSG的法向过载要小于PNG，因此可以视为IAVSG可以更合理地分配整个末制导段的法向过载。与图4、图5相比，采用IAVSG的法向过载曲线也完全消除了振荡现象。

图9所示为弹目视线角q的变化曲线，由于受到了抑制，因此采用IAVSG时q的变化明显要比采用PNG时小很多。

仿真得到PNG和IAVSG的脱靶量分别为2.473m和0.449m，说明在攻击机动目标时IAVSG的精度要远高于PNG。同时IAVSG也完全消除了变结构控制导致的抖振现象，有益于保持控制系统的稳定性。

5 结束语

本文提出的改进自适应滑模变结构导引律通过设计形式简单的变开关项系数并综合采用饱和函数法，兼顾了保证系统趋近速率和控制抖振的需求。该导引律具备了远优于比例导引律的精度，并实现了对末制导段导弹法向过载较为合理的分配，可以满足反坦克导弹对低空目标的作战需求。同时本文提出的变开关项系数的形式及消除抖振的方法对变结构导引律的研究也有一定的参考价值。

［1］程凤舟，陈士橹.拦截弹头的修正比例导引律［J］.空军工程大学学报，2003，4（4）：15－18.CHENG Feng－zhou，CHEN Shi－lu.An amendable proportional navigation law for intercepting warhead［J］.Journal of Air Force Engineering University，2003，4 （4）：15 － 18.（in Chinese）

［2］郭鹏飞，任章.一种攻击大机动目标的组合导引律［J］.宇航学报，2005，26（1）：104－106，111.GUO Peng－fei，REN Zhang.An integrated guidance law for target escapes with high acceleration［J］.Journal of Astronautics，2005，26（1）：104－106，111.（in Chinese）

［3］王辉，章虹虹.高精度偏置比例导引末制导律研究［J］.航天控制，2009，27（6）：19－22，32.WANG Hui，ZHANG Hong－hong.The development of highprecision biased proportional navigation terminal guidance control［J］.Aerospace Control，2009，27（6）：19－22，32.（in Chinese）

［4］HUNG Y W，GAN H J C.Variable structure control a survey［J］.IEEE Transactions on Industrial Electronics，1993，40（1）：2－22.

［5］BRIERLEY S D，LONGCHAM R.Application of sliding node control to air－air interception problem［J］.IEEE Transactions on Aerospace and Electronic Systems，1990，26（2）：306－325.

［6］RAVINDRA B K，SARMA I G，SWAMY K N.Switch bias proportional navigation for homing guidance against highly maneuvering targets［J］.Journal of Guidance，Control and Dynamics，1994，17（6）：1 357－1 363.

［7］ZHOU Di，MU Chun－di，XU Wen－li.Adaptive sliding－mode guidance of a homing missile［J］.Journal of Guidance，Control，and Dynamics，1999，22（4）：589－594.

［8］郭建国，周凤岐，周军.基于零脱靶量设计的变结构末制导律［J］.宇航学报，2005，26（2）：152－155，216.GUO Jian－guo，ZHOU Feng－qi，ZHOU Jun.Variable structure terminal guidance law based on zero miss－distance［J］.Journal of Astronautics，2005，26（2）：152－155，216.（in Chinese）

［9］杨军.红外寻的制导空空导弹变结构比例导引律研究［J］.西北工业大学学报，1998，16（1）：38－41.YANG Jun.A variable structure PN law suitable for high performance IR homing air to air missile［J］.Journal of Northwestern Polytechnical University，1998，16（1）：38－41.（in Chinese）

［10］宋建梅，张天桥.带末端落角约束的变结构导引律［J］.弹道学报，2001，13（1）：16－19.SONG Jian－mei，ZHANG Tian－qiao.The passive homing missile’s variable structure proportional navigation with terminal impact angular constraint［J］.Journal of Ballistics，2001，13（1）：16－19.（in Chinese）

［11］任义元，袁建平，方群.空空导弹变结构末制导律研究［J］.计算机仿真，2009，26（10）：25－29.REN Yi－yuan，YUAN Jian－ping，FANG Qun.A study of terminal variable structure guidance law of air－to－air missile［J］.Computer Simulation，2009，26（10）：25－29.（in Chinese）

［12］顾文锦，赵红超，杨智勇.变结构控制在导弹制导中的应用综述［J］.飞行力学，2005，23（1）：1－4.GU Wen－jin，ZHAO Hong－chao，YANG Zhi－yong.Application of variable structure control in missiles guidance［J］.Flight Dynamics，2005，23（1）：1－4.（in Chinese）

［13］佘文学，周军，周凤岐.一种考虑自动驾驶仪动态特性的自适应变结构制导律［J］.宇航学报，2003，24（3）：245－249.SHE Wen－xue，ZHOU Jun，ZHOU Feng－qi.An adaptive structure guidance law considering missile’s dynamics of autopilot［J］.Journal of Astronautics，2003，24（3）：245－249.（in Chinese）

［14］刘永善，刘藻珍，李兰忖.攻击机动目标的被动寻的模糊变结构 制 导 律 研 究 ［J］.系 统 工 程 与 电 子 技 术，2007，29（2）：254－258.LIU Yong－shan，LIU Zao－zhen，LI Lan－cun.Research on fuzzy variable structure guidance law for passive homing missiles against maneuvering targets［J］.Systems Engineering and Electronics，2007，29（2）：254－258.（in Chinese）