速度可调空空导弹鲁棒末制导律
史 鲲,梁晓庚
(西北工业大学 自动化学院,西安710072)
传统空空导弹末制导律多为比例导引律或者扩展的比例导引律,这种导引律结构简单、便于工程实现,但缺点是对于目标的大范围机动和初始条件的变化,其鲁棒性较差。
线性和非线性H∞鲁棒控制理论是处理包含不确定性和扰动系统控制问题的一种行之有效的方法[1],该方法不仅已经应用于飞行器自动驾驶仪的设计[2],许多学者也将其应用在导弹末制导律的设计中。如文献[3-4]通过求解哈密尔顿-雅克比偏微分不等式(HJPDI),得到了非线性H∞鲁棒制导律,但由于求解偏微分不等式十分困难,因此难以在实际工程中使用。郭建国等[5]提出了一种全局非线性H∞鲁棒末制导律,该方法利用李雅普诺夫稳定性理论严格证明了制导系统的全局渐近稳定性,无需求解复杂的HJPDI,通过数字仿真验证了该制导律具有较强的鲁棒性和较高的制导精度。但由于传统空空导弹以固体火箭发动机作为动力装置,导弹速度不可调节,因此并未对弹目相对运动速度进行控制。
当前,随着燃气流量调节技术的发展[6],变流量冲压发动机凭借其优越的性能,逐渐成为导弹的动力装置。例如欧洲的“流星”先进空空导弹,采用了可变流量的整体式固体火箭冲压发动机作为其动力装置[7],通过对燃气流量的调节,不仅可以扩大冲压发动机的有效工作范围,还可以调节推力的大小,从而改变导弹的径向加速度,实现真正的六自由度控制。
本文以速度可调空空导弹为背景,基于末制导律设计中的准平行接近原理,结合非线性H∞鲁棒控制方法,将目标机动看作外部扰动,设计了一种即具有较强鲁棒性,又能够充分发挥冲压发动机的推力调节能力,实现导弹快速攻击目的的非线性鲁棒末制导律。最后通过数字仿真与结果分析,验证了该制导律的性能和优势。
1 鲁棒末制导问题的数学描述
将导弹和目标看作质点,考查如图1所示的弹目相对运动示意图。图中,M和T分别表示导弹和目标。坐标系OX0Y0Z0为惯性坐标系,原点O与导弹重合。坐标系OXYZ为末制导视线坐标系,其中,OX轴与弹目视线重合,指向目标方向为正,OY轴处于铅垂平面内,向上为正,OZ轴按右手法则确定。两坐标系之间的转换关系由q和ψ2个角度表示,分别为弹目视线的俯仰角和方位角,即惯性坐标系经过两次旋转,就可与视线坐标系重合。
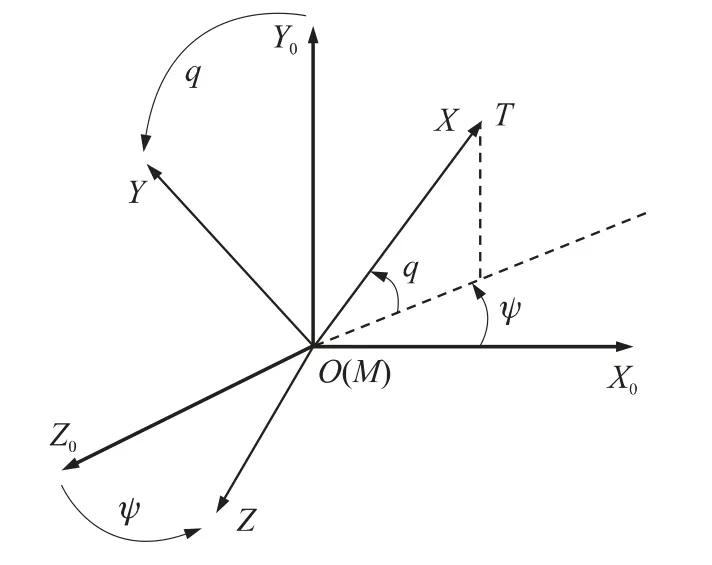
图1 弹目相对运动几何关系图
令r为弹目相对距离,ami和ati(i=x,y,z)分别为导弹和目标的加速度在视线坐标系上的分量,利用矢量的求导法则,可以得到三维弹目相对运动方程组[8]:
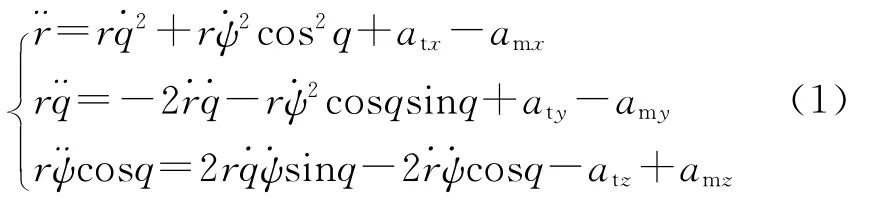
令
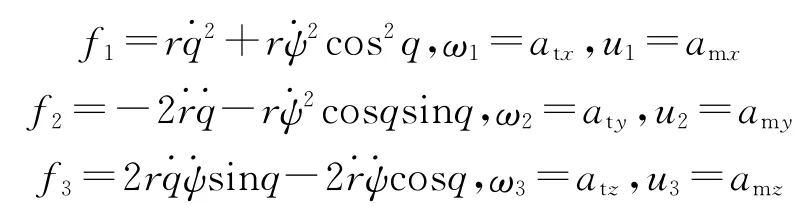
则式(1)所示的弹目相对运动学方程可改写为
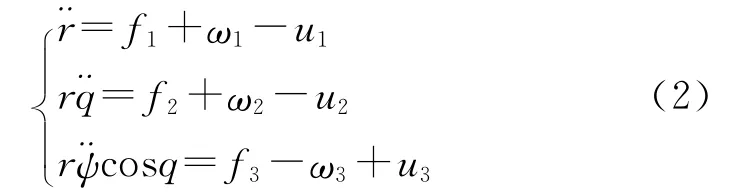
将式(2)中的uj(j=1,2,3)视为控制量,ωj(j=1,2,3)视为外部扰动,则H∞鲁棒末制导律设计问题就可以表述如下。
对于给定的系数γ,系统在导弹控制量u=(u1u2u3)T的作用下,在任意初始位置,对于有界外部扰动ω=(ω1ω2ω3)T,都有
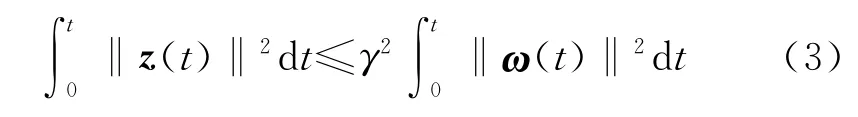
成立。式中:z为加权输出指标向量;系数γ表示对目标机动的敏感程度,一般选为γ≥1。
2 三维鲁棒制导律设计
考虑弹目相对运动方程式(2),将鲁棒制导律设计为如下形式:
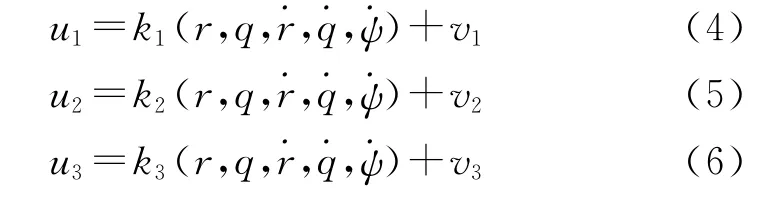
式中:kj,vj(j=1,2,3)待定。
根据制导律设计中的准平行接近原理,设计的鲁棒制导律应使弹目视线角速度尽量趋近于0,即→0,→0。又由于空空导弹采用可调推力的整体式固体火箭冲压发动机作为其动力装置,制导律还应该保证弹目相对速度在整个末制导拦截过程中至少不要衰减,从而缩短拦截时间。为此,令系统式(2)的加权输出指标向量为
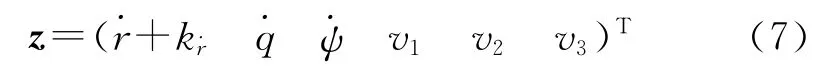
式中:+k项是为了保证足够大的弹目相对速度,k是一个大于0的常数,其值在后文中确定。选择v1,v2和v3项作为系统的输出量,目的是希望导弹所需要的机动能量最小。
根据李雅普诺夫理论,引入正定李雅普诺夫函数:
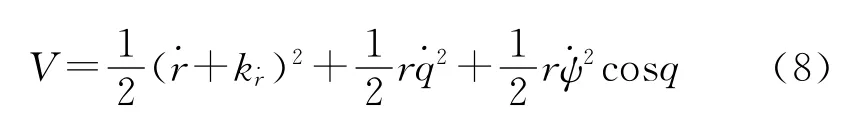
式中:|q|<π/2。对V进行求导,得:
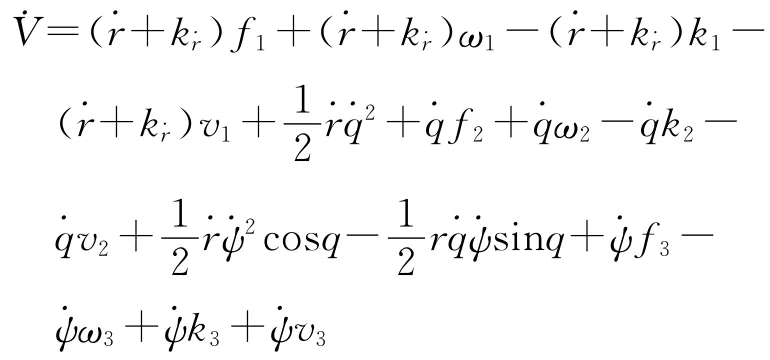
如果≤0,则闭环系统全局渐近稳定。再定义函数:
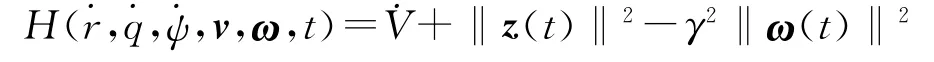
式中:v=(v1v2v3)T。由最优控制理论,对于不同的目标机动,解方程:
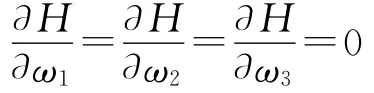
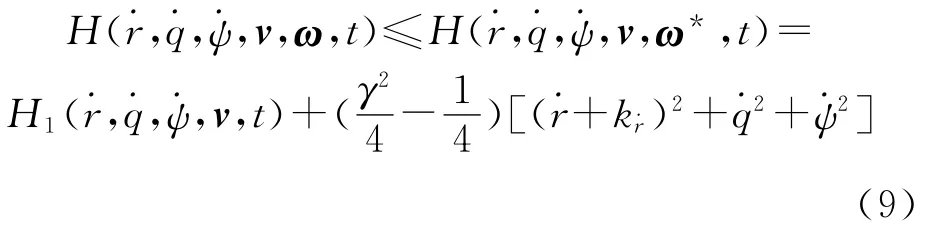
式中:

再考虑所需要机动的能量最小,解方程:
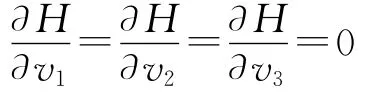
代入H1中,可得:
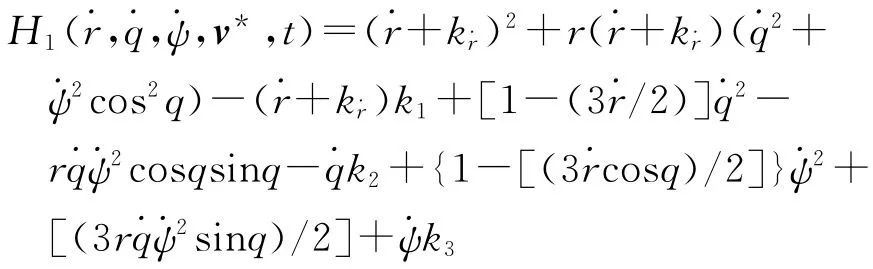
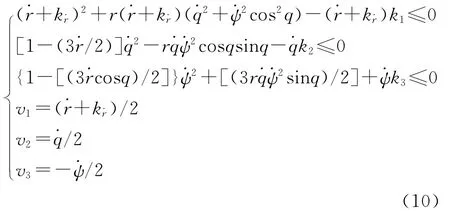
显然,当满足如下条件:时,有H1(,,,v,t)≤0。则 由 式(9),又 有γ≥1,可得H(,,,v,ω*,t)≤0。也就是在式(10)的 条件下,当γ≥1时,有:

由于
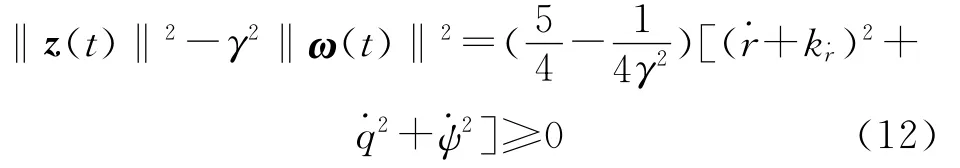
代入式(11)可得:
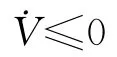
根据李雅普诺夫第二法可知,闭环系统是全局渐近稳定的。特别当系统扰动ω(t)=0,即目标不机动时,有:
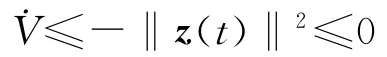
对式(11)两边积分得:
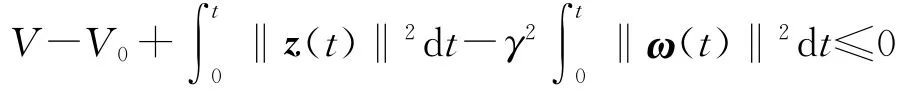
式中:V0为系统初始时刻的李雅普诺夫函数。由于制导律的设计采用了准平行接近原理,使得在整个末制导过程中,弹目视线俯仰角速度和方位角速度都非常小(2≈0,2≈0),则可以忽略式(8)中的后两项,那么如果0+k=0,就可以认为V0近似等于0;又由于弹目接近速度的变化在量级上比和大得多,则可以得出V-V0≥0。通过以上分析可知,如果令

就可以得到:
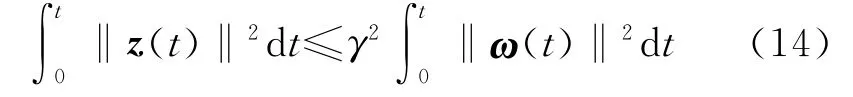
可得出如下结论:当如式(4)~式(6)所示的制导律满足式(10)时,该制导律具有H∞鲁棒性。由式(10)所示的条件,可以取
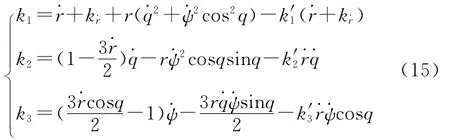
首先确定k′1。将k1代入式(10)中第一式,可得(+k)2k′1≤0,该式是要保证制导律对目标机动atx具有鲁棒性,因此选择:

再确定k′2和k′3。将k2代入式(10)中第二式,得2k′2≤0。由于在导弹飞向目标的过程中,<0,因此k′2的取值应不小于0。当ω(t)=0,将k2和v2=/2代入式(1),可得根据准平行接近理论,应保证趋近于0,由此,可得k′2的取值范围为

同样地,可求出k′3的取值范围为

k′2和k′3不仅保证了制导律对目标机动aty和atz的鲁棒性,还决定了实现角速度趋近于0的速度。但其取值并非绝对值越大越好,还应该结合导弹飞行中实际过载的能力,合理地选择k′2和k′3的取值。同样,k′1的取值也应考虑导弹过载和推力的限制。
至此,可以给出由式(4)~式(6)、式(10)、式(15)~式(18)所示的速度可调空空导弹非线性H∞鲁棒末制导律。
对于参数k的选择,式(13)可以解释为希望导弹通过改变自身的速度,在整个末制导过程中保持末制导初始时刻的弹目相对速度而不衰减,从而以较短的时间击中目标。然而,该选择将导致一个严重的问题,即当目标本身的机动使得弹目相对速度的绝对值||增大时,制导律将使导弹在视线方向上减速,反而增加了导弹的拦截时间。为此,对制导律的第一项u1做如下修正,即当||-|0|≥0,也就是弹目相对速度大于或等于初始相对速度时,令u1=0;当||-|0|<0时,u1等于按照前述制导律解算所得值。这样一来,可以保证导弹的拦截时间:

3 末制导律仿真及分析
考虑纵向平面内的拦截问题,设定导弹和目标的仿真初始条件如下。
导弹的位置为惯性坐标系下Xm0=0;Ym0=5km;导弹的初始速度vm0=1 200 m/s,弹道倾角θm0=0;目标的位置为惯性坐标系下Xt0=10km,Yt0=10km;目标的初始速度vt0=300m/s,弹道倾角θt0=π;目标在弹道坐标系(O2X2Y2Z2)下的切向加速度和法向加速度分别为atx2= -20m/s2和aty2=-80m/s2,也就是说,目标不仅具有改变速度方向的机动,还具有改变速度大小的机动。
制导律中参数的选择为k′1=-0.1,k′2=1,k′3=-1。
为了将本文设计的末制导律(TGL1)与不控制弹目相对速度的末制导律(TGL2)(即式(4)中u1=0)相比较,在相同的初始条件下,先后对2种制导律进行了仿真。仿真对比结果如图2~图5所示。
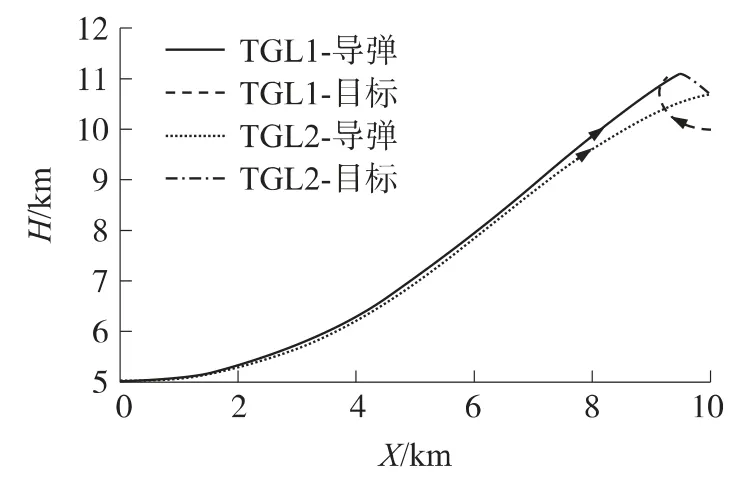
图2 弹目相对运动轨迹对比图
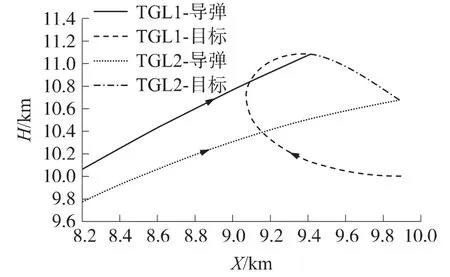
图3 命中点放大图
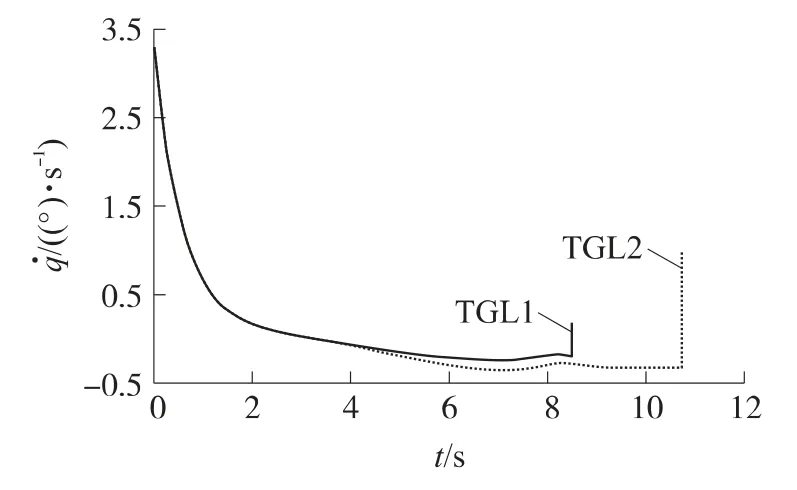
图4 视线角速度对比图
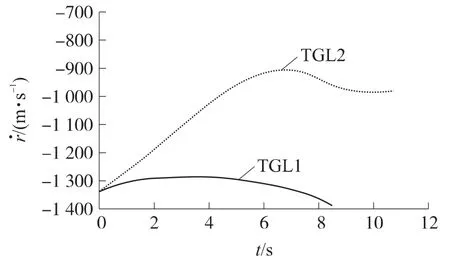
图5 弹目相对速度对比图
图2为2种制导律仿真所得的弹目相对运动轨迹对比图。从图中可以看出,与不控制弹目相对速度的末制导律相比,本文设计的末制导律在弹道上更为平滑一些。从图3所示的命中点放大图可以看到,尽管2种末制导律都能以较高的精度(TGL1的脱靶量为0.199m,TGL2的脱靶量为0.465m)命中目标(从图4中可以看出,2种末制导律都能将视线角速度控制在0(°)·s-1附近),但本文设计的末制导律在拦截时间上却具有明显的优势,二者相差将近2s。这一点也可从图5所示的弹目相对速度对比图中得到说明。在不控制弹目相对速度的制导律的作用下,弹目相对速度的绝对值衰减较大,而本文设计的末制导律能使弹目相对速度几乎保持在一个常值,体现了其优势。
4 结束语
本文针对采用可变流量固体火箭冲压发动机作为动力系统的速度可调空空导弹,基于非线性H∞鲁棒控制思想,通过选择合适的李雅普诺夫函数,不仅保证了制导系统大范围渐近稳定,还推导出了能够控制弹目相对速度的鲁棒末制导律。数字仿真表明,该制导律对于目标大范围机动具有较强的鲁棒性,制导精度较高,明显缩短了导弹拦截时间,能够充分发挥先进动力系统的特点和优势,具有一定的前瞻性和工程应用参考价值。如何将该制导律与冲压发动机推力调节控制、气动舵控制相结合,是今后研究的重点。
[1]梅生伟,申铁龙,刘志康.现代鲁棒控制理论与应用[M].北京:清华大学出版社,2003.MEI Sheng-wei,SHEN Tie-long,LIU Zhi-kang.Modern robust control theory and application[M].Beijing:Tsinghua University Press,2003.(in Chinese)
[2]GOMAN M,SIDORYUK M,USTINOV A.Control law designs for flexible aircraft:comparison of theH∞-based and classical methods,AIAA2005-6265[R].2005.
[3]李新国,陈士橹.非线性H∞鲁棒制导律设计[J].宇航学报,2000,21(增刊):48-51.LI Xin-guo,CHEN Shi-lu.Study of nonlinearH∞robust guidance law[J].Journal of Astronautics,2000,21(S):48-51.(in Chinese)
[4]CHEN H Y.3DnonlinearH∞/H2law with dissipative theory,AIAA2002-5024[R].2002.
[5]郭建国,周军.基于H∞控制的非线性末制导律设计[J].航空学报,2009,30(12):2 423-2 427.GUO Jian-guo,ZHOU Jun.Design ofH∞control based nonlinear terminal guidance law[J].Acta Aerodynamica et Astronautica Sinica,2009,30(12):2 423-2 427.(in Chinese)
[6]牛文玉.燃气流量可调的固体火箭冲压发动机控制方法研究[D].哈尔滨:哈尔滨工业大学,2009.NIU Wen-yu.Study on control methods for variable flow ducted rockets[D].Harbin:Harbin Institute of Technology,2009.(in Chinese)
[7]曹军伟,王虎干.固体火箭冲压发动机在空空导弹上应用的优势[J].航空兵器,2009(2):47-49.CAO Jun-wei,WANG Hu-gan.Predominance of ducted solid rocket ram jet applied to airborne missile[J].Aero Weaponry,2009(2):47-49.(in Chinese)
[8]佘文学,周凤岐.三维非线性变结构寻的制导律[J].宇航学报,2004,25(6):681-685.SHE Wen-xue,ZHOU Feng-qi.High precision 3-D nonlinear variable structure guidance law for homing missile[J].Journal of Astronautics,2004,25(6):681-685.(in Chinese)

