固体火箭发动机零维两相内弹道研究

陈 军

（南京理工大学 机械工程学院，南京210094）

随着高能推进剂在火箭发动机中的普遍应用，两相流动对发动机性能的影响越来越受到重视。文献[1]在前人研究的基础上，深入研究了一维两相内弹道的模型与计算方法，文献[2]得出了火箭喷管在两相流动下可以显式计算的性能公式。

一维两相内弹道在计算与应用上显得较复杂，而工程中常采用能够快速计算的零维内弹道模型[3]。本文采用文献[2]的两相流性能公式，构造了零维两相内弹道模型，并与纯气相零维内弹道模型进行了对比计算，分析了它们的变化特性和预示精度。

1 固体火箭发动机零维两相内弹道的微分方程

为使问题简化，在建立零维内弹道计算方程时作如下假设：

①对凝聚相微粒的基本假设是，凝聚相微粒是具有均一尺寸的单分散混合物，即将按质量平均的凝聚相微粒半径作为整个微粒群的半径，不存在微粒间的相互作用及相变，而仅考虑气相与凝聚相之间的气动作用项和传热项；

②推进剂在燃烧室内完全燃烧，并且燃烧过程中燃烧温度不变；

③推进剂燃烧的气相产物是组分不变的理想气体。

为建立计算压强的内弹道公式，需要考虑燃气质量的变化规律。根据质量守恒原理，燃烧室内燃气的质量mm（包括气相质量mg与凝聚相质量mc）随时间的变化率应等于燃烧室内燃气生成率b与燃气从喷管排出的质量流率之差，即

燃烧室中的燃气质量mm可以表示为

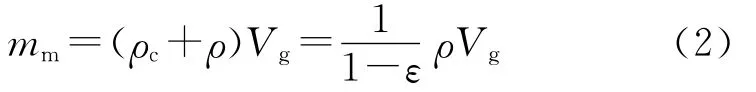
式中：ρc为凝聚相的平均密度，ρ为气相的平均密度，Vg为燃气在燃烧室中的自由容积，ε为凝聚相质量比。微分式（2），得：

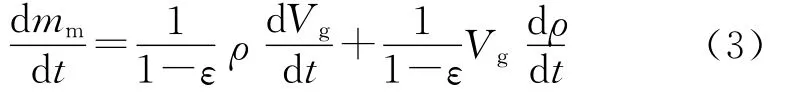
式中：Ab，分别为推进剂装药的燃烧面积和燃烧速度。

密度的变化按状态方程可以转化为零维平均压强p的变化关系，故式（3）可以变为

式中：χ为燃气温度T的修正系数，R为燃气的气体常数。

燃气生成率为

式中：ρp为推进剂密度。

将式（5）和式（6）代入式（1），可得零维两相内弹道微分方程：

或

与纯气相的零维内弹道微分方程相比，零维两相内弹道微分方程中多了修正项1－ε，同时喷管质量流率为两相流动的质量流率。实际上，零维两相内弹道微分方程的本质是，影响压强变化的各项均是混合流动中的气相因素。当ε→0时，则与纯气相的零维内弹道微分方程相同。

由于ρ≪ρp，零维两相内弹道微分方程可近似为

类似分析，可知零维两相内弹道后效段方程为

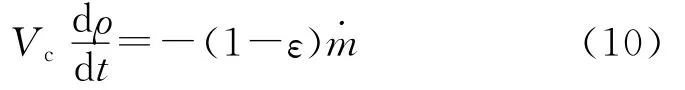
式中：Vc为燃烧室容积。

2 零维两相内弹道中的两相特性参数

在零维两相内弹道模型中，涉及到的两相特性参数包括凝聚相质量比ε和两相质量流率。

目前绝大多数推进剂添加的金属燃烧剂为铝粉。由文献[1]，推进剂中Al的质量分数w（Al）在小于15%时与对应燃气中的凝聚相（Al2O3）质量比ε可近似为线性关系，即

在w（Al）＝（0～26.92）%时，凝聚相质量比ε为

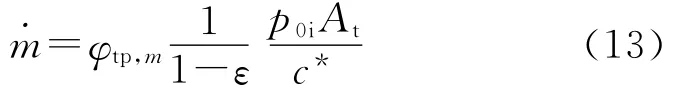
式中：p0i为喷管入口总压，由文献[3]给出的近似结果有p0i＝p；At为喷管喉部截面积；c＊为特征速度；系数φtp，m为两相流的流量系数，表达式为[2]

由文献[2]可知喷管的两相质量流率公式为

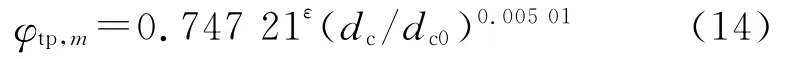
式中：dc为凝聚相粒子直径（μm）；dc0为凝聚相参考粒子直径，dc0＝0.52μm。为此，还需要确定凝聚相直径dc的大小。

这里采用文献[4]中的平均粒子尺寸估算公式，即

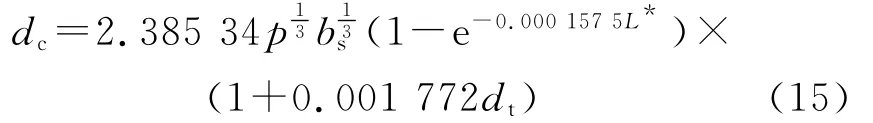
式中：bs为凝聚相微粒的质量摩尔浓度（mol/0.1kg）；L＊为发动机的特征长度（mm），即L＊＝Vg/At；dt为喷喉直径（mm）；p为燃烧室压强（MPa）。

在一定的凝聚相质量比ε下，凝聚相微粒的质量摩尔浓度bs与粒子的平均直径dc有关。不考虑相变，考虑凝聚相的质量mc是由单个粒子质量mci组成，即有

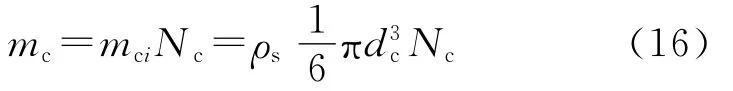
代入式（15），得粒子的平均直径dc为

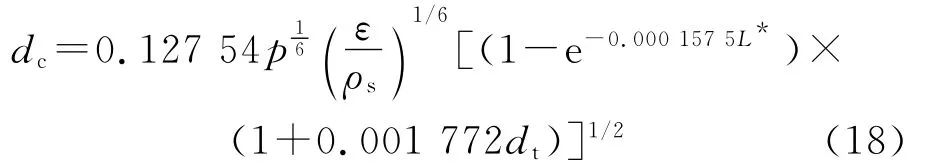
3 零维两相内弹道的平衡压强

当燃气生成率等于喷管质量流率时，压强处于平衡状态，即dp/dt＝0，由内弹道方程（8），可得：

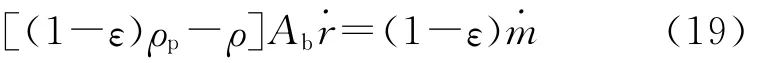
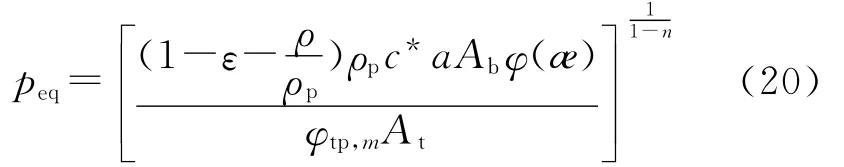
由于ρ/ρp≪1，平衡压强公式可近似为

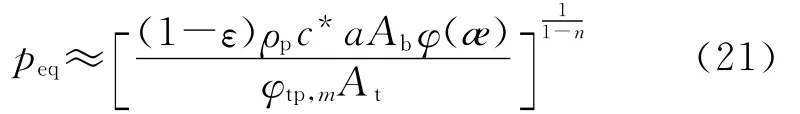
由于粒子的平均直径dc与压强还存在一定量的变化关系，故两相流量系数φtp，m与压强也存在变化关系。将式（18）代入式（14）可得流量系数φtp，m：

式中：系数Ctp为

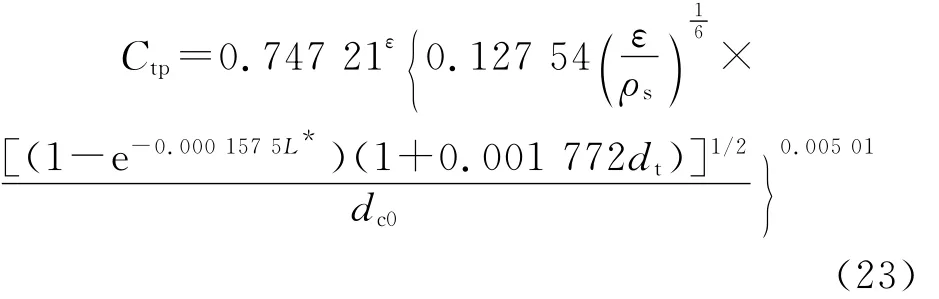
从压强指数0.000 835可知，压强对两相流的流量系数影响很小，简化计算时可以忽略不计。

将式（22）代入平衡压强公式（20）和式（21），得：

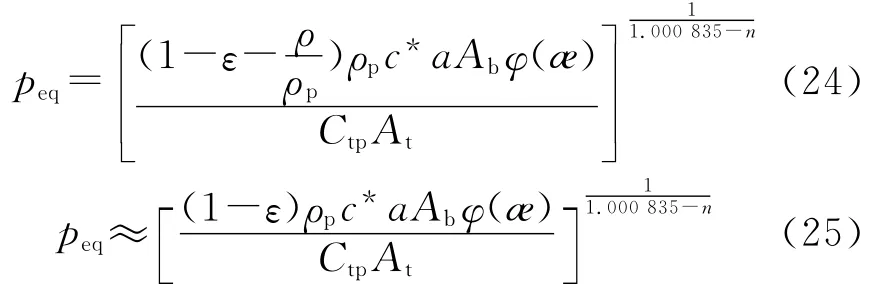
定义装填参量M为

则平衡压强公式可表示为

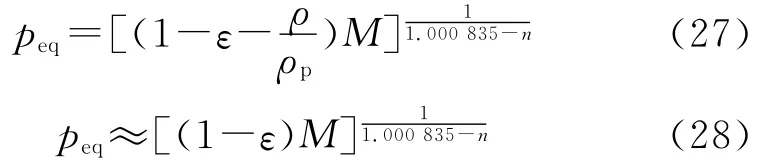
近似式（28）可显式地直接计算平衡压强，而式（27）中由于包含有密度ρ项，不能直接计算，是隐式方程，需要迭代求解。为提高简化计算的精度，可对式（27）中的密度ρ项展开为幂级数，并忽略高阶项，可得

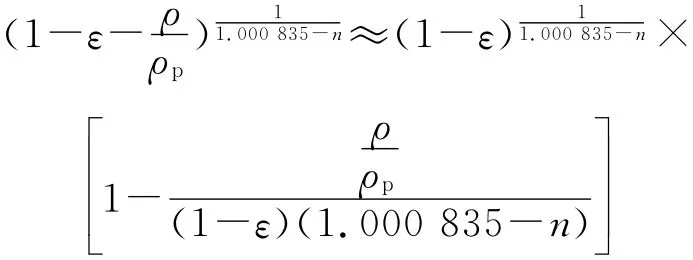
于是，式（27）变为

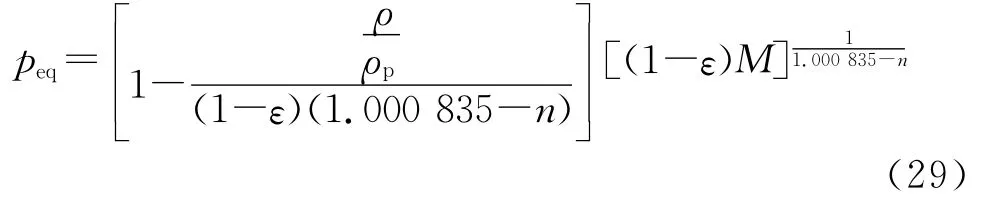
代入状态方程，可得显式的精度更高的平衡压强公式为

计算表明，式（30）的计算结果更精确，式（28）的计算结果与之相比误差为2%左右。

利用零维两相内弹道的平衡压强公式，可以大大简化火箭设计过程中对两相内弹道压强的计算，有效提高设计精确度。

4 零维两相内弹道的计算与分析

为求解零维两相内弹道微分方程，需要对式（8）进行变形，则

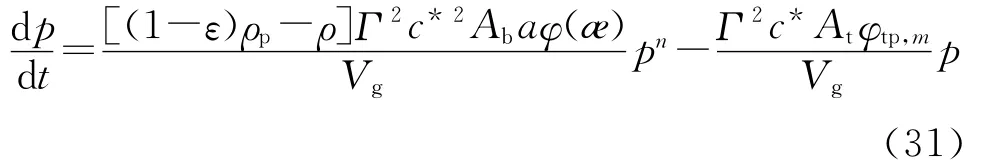
零维两相内弹道计算的主要过程：

①根据选用的不同推进剂，由式（11）或式（12）得到相应的凝聚相质量比ε；

②给定初始时间、初始压强等初始条件和时间步长等参数；

③计算当前时刻装药的几何参数，由式（18）计算粒子的平均直径dc，再由式（14）计算对应的两相流量系数φtp，m；

④利用龙格－库塔法解零维两相内弹道的微分方程式（31），得到下一时刻的压强；

⑤重复上述过程，直到计算出全部时刻对应的压强。

求解时，考虑到燃烧室中的温度假设是不变的，即有T＝T0＝Const。

为检验上述模型的有效性与正确性，计算了某远程固体火箭发动机[1]的内弹道。该发动机采用两级装药（星孔＋圆孔）；推进剂为含铝5%的丁羟复合推进剂，由式（11）可知，燃气的凝聚相质量比ε＝9.322%；凝聚相为液态 Al2O3，其密度ρs＝3.0×103kg/m3[6]。

对微分方程（31）求解，在准定常条件下，得到压强－时间曲线，如图1所示。由图可见，计算结果与实验数据吻合很好。计算得到的头部压强平均值与实验值的误差为0.3%，具有较好的计算精度。

计算得到的推力（F）－时间曲线如图2所示。由图可见，计算结果与实验数据吻合很好。计算得到的平均推力与实验值的误差为2.2%，同样具有满意的计算精度。

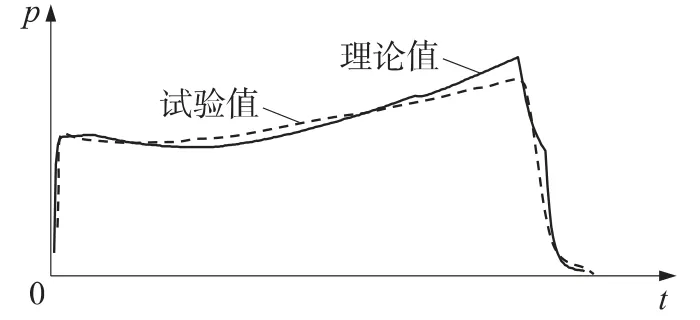
图1 某远程火箭零维两相p－t曲线

图2 某远程火箭零维两相F－t曲线

如果不考虑两相流动，采用纯气相流动假设，在相同条件下，得到的计算曲线如图3和图4所示，可见吻合程度较低。计算得到的头部压强平均值与实验值的误差为7.8%，推力的误差值为5.4%，误差明显增大，达不到一般的工程计算要求，这正是由于纯气相理论模型忽略了凝相对流动的影响。

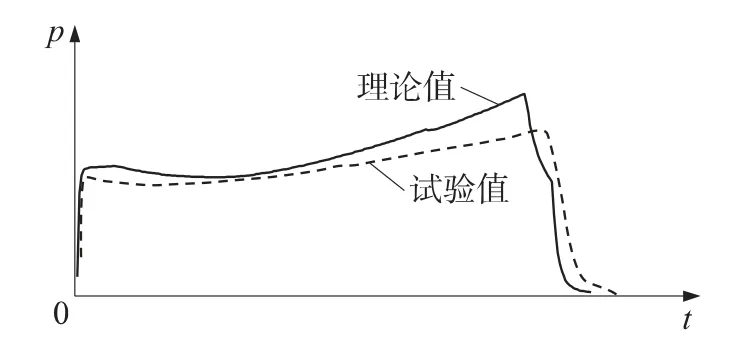
图3 某远程火箭纯气相零维p－t曲线

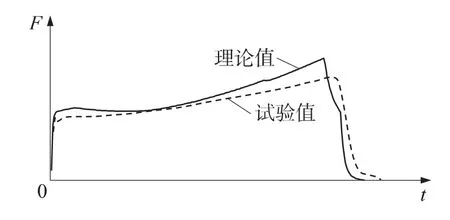
图4 某远程火箭纯气相零维F－t曲线

比较零维两相内弹道与纯气相零维内弹道的微分方程可知，考虑两相流动实际上是对流量的修正：对燃气生成量的修正系数为1－ε；对喷管质量流率的修正系数为φtp，m。本文给出的计算实例可以计算相应的修正量为1－ε＝0.91，φtp，m＝1.06。实际上，参考修正系数φtp，m的大小，利用纯气相内弹道方程，通过流量修正的办法也可以降低纯气相内弹道的计算误差。图5为通过修正后的纯气相内弹道压强－时间曲线，对喷管流量的修正系数为1.07，可见，与实验数据的吻合程度大大提高。计算得到的头部平均压强与实验值的误差为0.9%，精度明显提高。

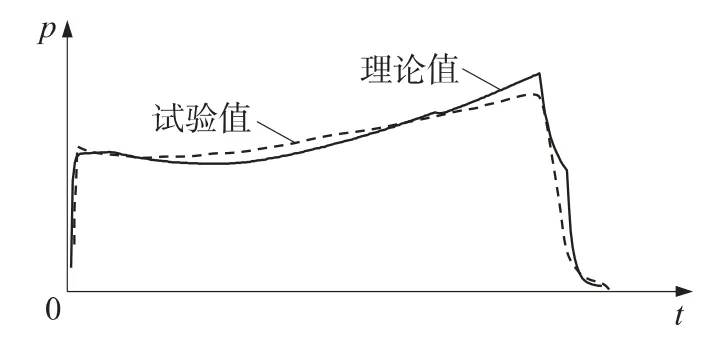
图5 某远程火箭修正后的纯气相零维p－t曲线

再讨论平衡压强的计算。利用近似公式（28）计算得到燃烧结束时刻的平衡压强为18.80 MPa，而式（30）计算得到对应时刻的平衡压强为18.44 MPa，利用微分方程求解的对应平衡压强为18.55 MPa。以微分方程的求解结果作为参照，可知近似式（28）的计算误差为1.4%，而式（30）的计算误差为0.6%，更为精确。

与纯气相平衡压强公式相比，零维两相内弹道的平衡压强公式中包含了两相特性参数1－ε和Ctp对计算的修正。本文给出的计算实例得出Ctp＝0.96。

5 结论

通过对构建的零维两相内弹道模型的计算与对比分析，可以得出如下结论：

①建立的零维两相内弹道模型是适当的，计算表明该模型可以有效地降低纯气相模型引起的理论与实际之间的模型偏差，使得内弹道的预示精度大大提高；

②与纯气相零维内弹道模型相比，零维两相内弹道微分方程中凝聚相对内弹道的影响实际上是对流量的修正：对燃气生成量的修正系数为1－ε，对喷管质量流率的修正系数为φtp，m，对平衡压强的影响包括1－ε和Ctp两项；

③与一维两相内弹道模型相比，采用零维两相内弹道模型的计算工作量大大减小；与纯气相零维内弹模型相比，增加的计算工作量很少，只需对计算程序做少许改动。

[1]陈军，封锋，余陵.固体火箭发动机一维两相内弹道研究[J].弹道学报，2010，22（3）：16－20.CHEN Jun，FENG Feng，YU Ling.Research on one－dimensional two－phase internal ballistics of SRM[J].Journal of Ballistics，2010，22（3）：16－20.（in Chinese）

[2]陈军.火箭喷管两相流动性能计算公式[J].弹道学报，2012，24（1）：69－74.CHEN Jun.Properties’formulae of rocket nozzle with one－dimensional two－phase flow [J].Journal of Ballistics，2012，24（1）：69－74.（in Chinese）

[3]武晓松，陈军，王栋.固体火箭发动机原理[M].北京：兵器工业出版社，2011：236－243.WU Xiao－song，CHEN Jun，WANG Dong.Principles of solid rocket motor[M].Beijing：Ordnance Industry Press，2011：236－243.（in Chinese）

[4]COATS D E.A computer program for the prediction of solid propellant rocket motor performance，AD－A－015140[R].1975.

[5]凌永祥，陈明逵.计算方法教程[M].西安：西安交通大学出版社，2005：263－273.LING Yong－xiang，CHEN Ming－kui.Computational methods course[M].Xi’an：Xi’an Jiaotong University Press，2005：263－273.（in Chinese）

[6]AHUJA R，BELONOSHKO A B，JOHANSSON B.Melting and liquid structure of aluminum oxide using a molecular－dynamics simulation[J].Phys Rev E，1998，57：1673.