基于目标坐标系的高超声速无动力滑翔能态方程

闫晓东，王 智

（西北工业大学 航天学院，西安710072）

发展具有超远程、快速打击能力的战略武器系统一直是各军事大国的兴趣。由于弹道导弹易于被探测，而且随着反导技术的发展，弹道导弹的作战效能逐渐降低，近年来，采用高超声速滑翔飞行器替代弹道导弹完成远程打击任务日益受到重视。美国国防部和空军2003年联合推出了“猎鹰”（Falcon）计划，该计划提出的通用航空飞行器（CAV）是一种采用助推火箭发射的升力体外形高超声速滑翔飞行器，依靠气动力控制，可跨大气层无动力滑翔飞行［1－2］。

高超声速滑翔飞行器采用升力式外形，依靠气动力控制，可跨大气层无动力滑翔飞行，从而实现快速远程攻击。由于高超声速滑翔过程十分复杂，其作战任务又具有多样性与灵活性，对制导系统的自主性、自适应性都提出了很高的要求。在线轨迹规划是提高制导系统自适应性的有效途径。一般在线轨迹规划过程中，均需要对动力学方程进行积分以获取相关参数，因此，动力学方程的形式对于轨迹规划算法的复杂度和计算效率具有重要影响。

文献［3］提出了一种将目标平面地心固连坐标系作为参考坐标系的动力学方程，该动力学方程忽略了地球旋转的影响，尽管简化了方程形式，但是对于长时间、超远程高超声速滑翔飞行，其误差较大。本文将目标平面坐标系作为参考坐标系，推导了三自由度无动力滑翔能态方程，并考虑了地球旋转的影响。该能态方程使得原终端时间自由问题转化为定积分区间问题，且动力学方程的状态变量量级相同，有效提高了轨迹规划及优化的数值效率。此外，纵程和横程是轨迹规划的重要规划变量，该能态方程的状态变量经度和纬度直接表征了纵程和横程，有效提高了轨迹规划的便利性。

1 坐标系的定义及变换

三自由度无动力滑翔动力学方程一般建立在弹道坐标系中，以地心固连坐标系为参考坐标系。

地心固连坐标系：坐标系原点为地心O，OXe轴在赤道平面内指向格林威治子午线，OZe轴垂直于赤道平面指向北极，OXeYeZe构成右手直角坐标系。

设再入点Oi（θ0，φ0）为对应的星下点经纬度；再入段终点Of（θf，φf）为对应的星下点经纬度。现将地心固连坐标系的赤道平面重新定义为目标平面，即包含再入点Oi、终点Of的地球大圆平面，如图1所示。

图1 坐标系示意图

转换后的地心固连坐标系（以下称为目标平面坐标系）原点为地心O，轴由地心指向再入点星下点Oi，轴垂直于参考再入平面，其方向为沿着轴看去，目标Of在Oi的顺时针方向。构成右手直角坐标系。

地心固连坐标系和目标平面坐标系对应的球坐标之间的转换关系为

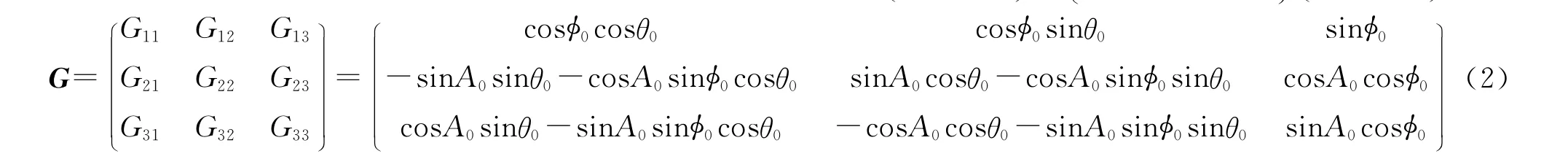
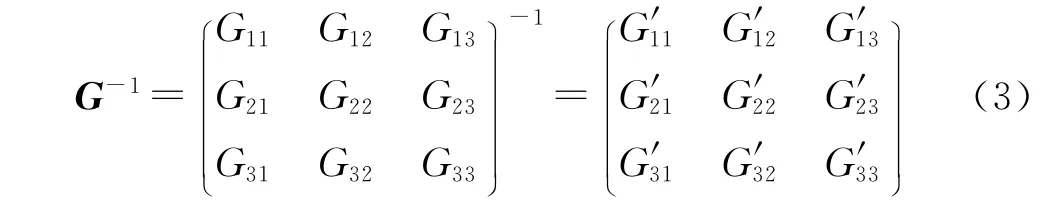
式中：A0为再入点瞬时纵向平面与正北方向的夹角，即视线角，从正北顺时针转到视线为正；φ0和θ0分别为再入点地心纬度和再入点经度。当A0、φ0、θ0确定后，G为常数矩阵。

2 无动力三自由度动力学方程

2.1 动力学方程

不考虑地球旋转，假设飞行器的侧滑角为0，无动力三自由度质点动力学方程为［4－5］

上述动力学方程组中有6个状态变量：r，θ，φ，v，γ，ψ。r为地球球心到飞行器质心的距离；θ为经度；φ为纬度；v为相对地球速度；γ为速度倾角；σ为速度倾侧角；速度方位角ψ＝0表示正北方向，从正北顺时针旋转为正；ωd为地球旋转角速度；aD，aL分别为阻力加速度和升力加速度，可由下式给出：

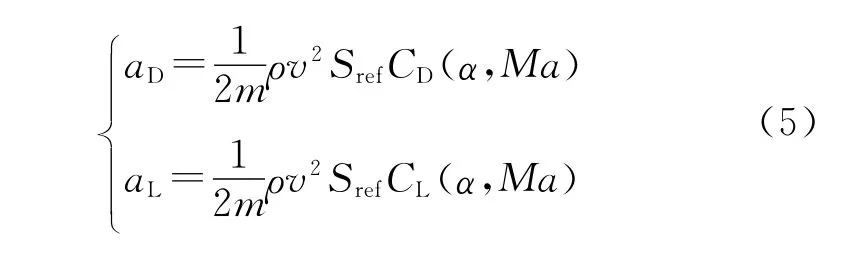
式中：CD，CL分别为飞行器的阻力系数和升力系数，它们是攻角α和马赫数Ma的函数；Sref为飞行器参考面积；ρ为大气密度。

2.2 目标平面坐标系下的动力学方程

在目标坐标系中，纵向运动参数不变，即（后面公式中均采用原符号）：

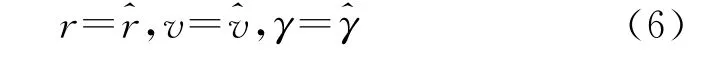
横向运动参数与地心球面固连坐标系的运动参数θ、φ的关系式由式（1）确定。与ψ之间的关系为

由式（1）、式（3）可得：

由式（8）可得：

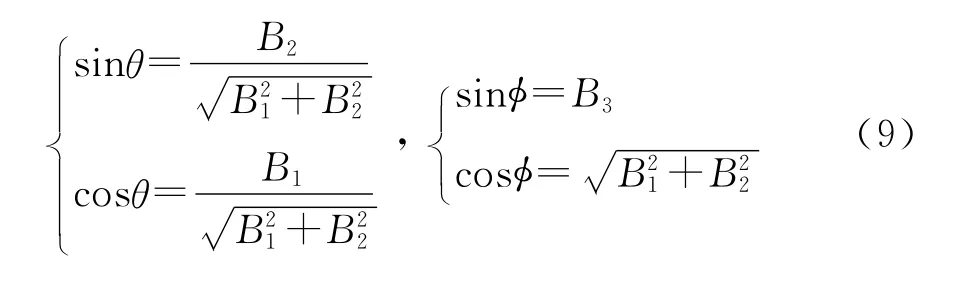
由式（1）可得：

对式（10）求导，并整理得到目标平面坐标系下的动力学方程为

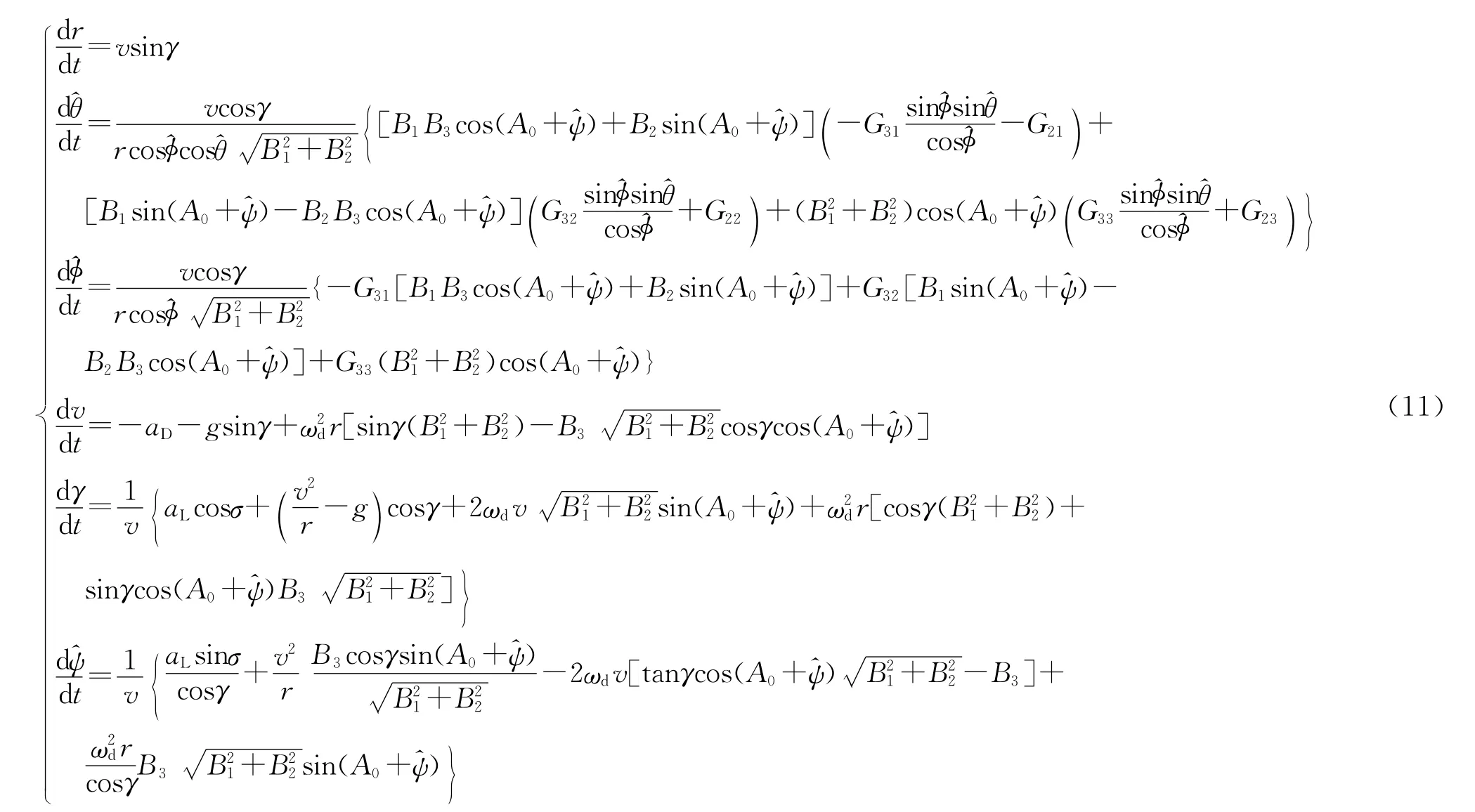
3 目标平面坐标系下的三自由度无动力能态方程

在高超声速滑翔飞行器的无动力飞行中，沿着轨迹能量是单调减小的，这使得能量是比时间更合适的控制变量。设能量E为

式中：Rd为地球平均半径，μ为地球引力常数。由式（12）可知，v可以表示为E和r的函数，从而飞行器运动方程中的速度微分方程可以去掉，飞行器运动方程由六阶降为五阶。式（12）两边同时对时间求导，有：

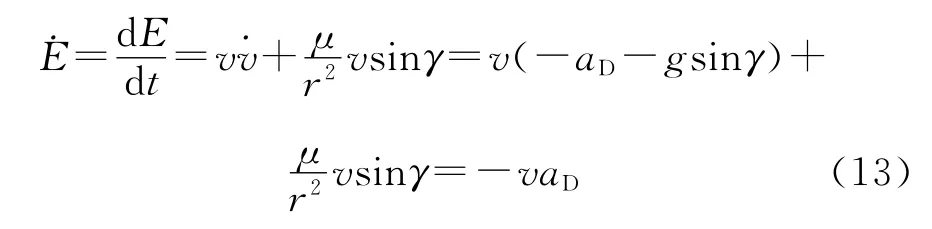
利用如下关系：

可将飞行器各运动状态变量对时间的导数变为对能量的导数。

为了提高数值计算的效率，对能量E进行归一化处理。令：

式中：E0为再入初始时刻的能量，Ef为终端时刻的能量。归一化处理后，初始能量为0，终端能量为1，即e0＝0，ef＝1。将r采用Rd进行归一化，即＝r／Rd，结合式（11）、式（14）、式（15），可得目标坐标系中以归一化能量为自变量的能态方程为

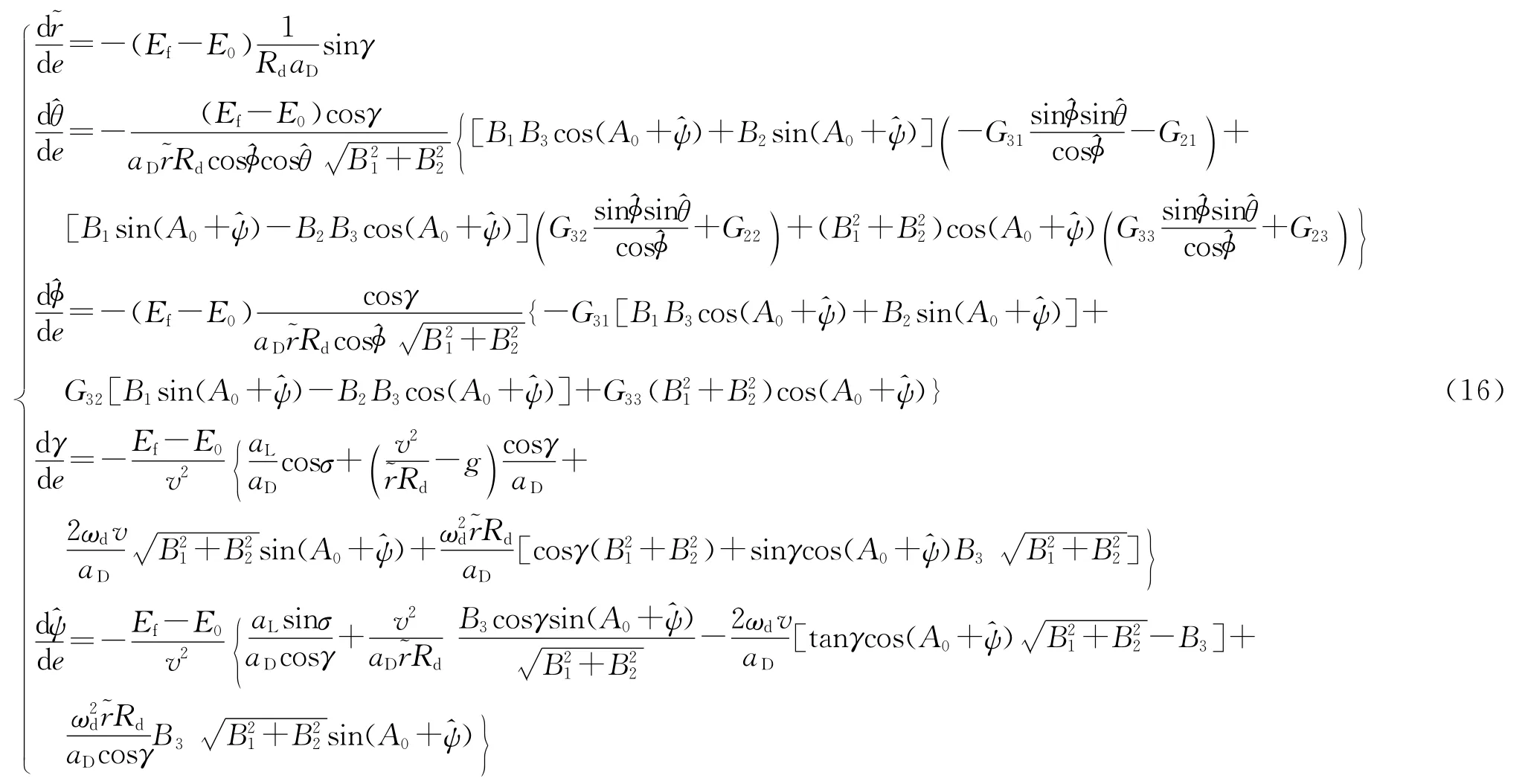
4 算例

4.1 初始条件

仿真计算以CAV－L为对象［6］，气动系数见文献［6］，飞行器质量m＝907.0kg，特征面积Sref＝0.35m2，h0为初始高度。状态初值见表1和表2。

表1 地心球面固连坐标系状态初值

表2 目标坐标系状态初值

仿真终端轨迹参数：θf＝179.504°，φf＝28.61°，hf＝20km，vf＝1 800m／s。目标坐标系下，＝0°，＝58.653 3°，预定航程s＝Rd＝6 531km。

4.2 仿真结果

在目标坐标系下采用该能态方程的仿真结果如图2～图5所示。不难发现，以归一化能量为独立变量的能态方程积分区间为［0，1］，动力学方程积分状态的数量级相似。由于目标平面坐标系下纵程和横程可由经度和纬度直接计算得到，因而动力学方程的状态变量经度表征了纵程，纬度表征了横程，如图2所示。

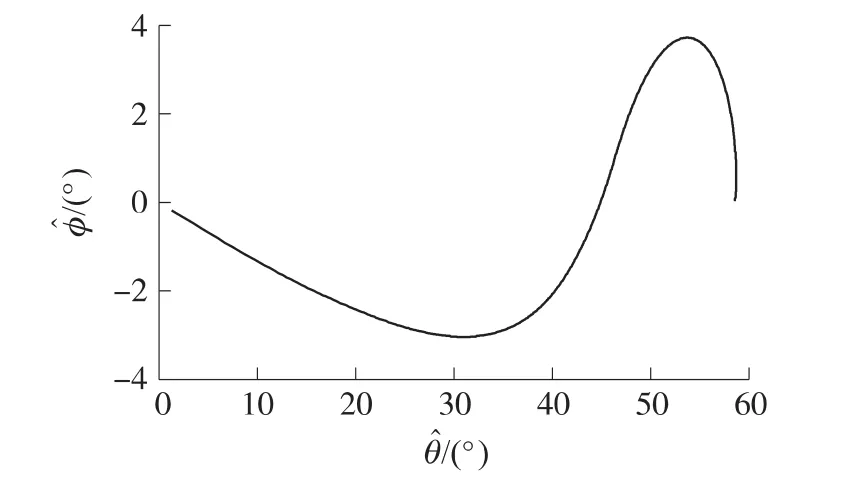
图2 地面轨迹曲线

图3 航向角曲线

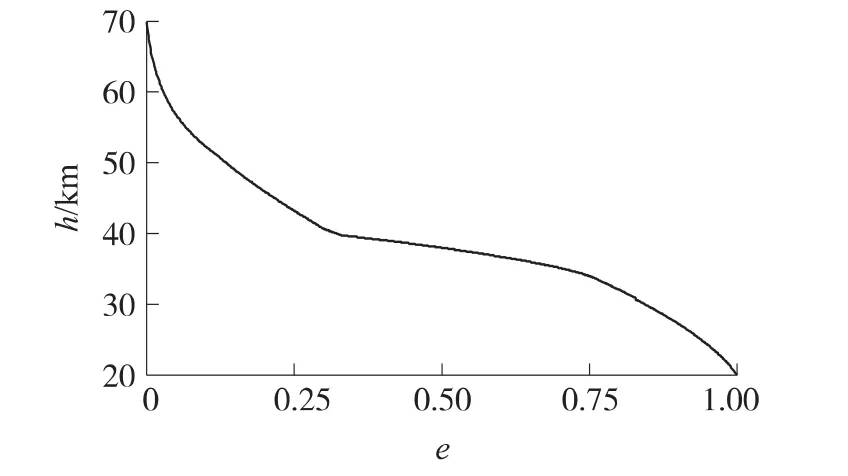
图4 高度曲线

图5 速度曲线

5 结束语

高超声速滑翔飞行器具有很高的机动能力，可以实现超远程打击任务。在其无动力滑翔过程中，需要考虑诸多约束，如过程约束、终端约束以及地理约束等，因而多约束条件下的弹道规划和优化是高超声速滑翔飞行器任务分析、制导方法研究的重要内容。在弹道规划和优化设计中，由于动力学方程的高度非线性，动力学方程的求解只能采用数值解法，因此动力学方程要尽可能提高数值求解效率，便于规划问题的求解。本文推导了目标平面坐标系下的归一化能态方程，尽管方程形式较为复杂，但有助于提高数值计算效率，便于弹道规划。

［1］WALKER S H，RODGERS F.Falcon hypersonic technology overview，AIAA 2005－3253［R］.2005.

［2］WALKER S H，SHERK J.The DARPA／AF falcon program：the hypersonic technology vehicle＃2（HTV－2）flight demonstration phase，AIAA 2008－2539［R］.2008.

［3］MEASE K D，CHEN D T，TEUFEL P.Reduced－order entry trajectory planning for acceleration guidance［J］.Journal of Guidance，Control，and Dynamics，2002，25（2）：257－266.

［4］闫晓东，唐硕.亚轨道飞行器返回轨道设计方法研究［J］.宇航学报，2008，29（2）：467－471.YAN Xiao－dong，TANG Shuo.An alternative method of entry trajectory design for suborbital launch vehicle［J］.Journal of Astronautics，2008，29（2）：467－471.（in Chinese）

［5］赵汉元.飞行器再入动力学和制导［M］.长沙：国防科技大学出版社，1997.ZHAO Han－yuan.Entry dynamics and guidance of flight vehicle［M］.Changsha：National University of Defense Technology Press，1997.（in Chinese）

［6］PHILLIPS T H.A common aero vehicle（CAV）model，description，and employment guide［R］.Schafer Corporation for AFRL and AFSPC，2003.