高速旋转弹飞行姿态磁测解算方法

龙达峰，刘 俊，2，张晓明，李 杰

（中北大学1.电子测试技术重点实验室；2.仪器科学与动态测试教育部重点实验室，太原030051）

常规弹药制导化、灵巧化改造是当今常规弹药技术发展的主流方向，弹体飞行过程中姿态角的实时精确测量是实现其精确控制飞行的前提与技术瓶颈[1－2]。受常规弹药的高旋转、高冲击、小体积等恶劣应用环境的限制，所选用的导航传感器必须满足抗高过载、小体积、量程与精度合适等需求，能采用的姿态传感器甚少，主要有 MEMS陀螺仪、太阳方位角传感器、地磁场传感器等[3－4]。以地磁场作为测量基准，通过磁传感器在弹体内的适当布阵，由相关算法解算弹体姿态参数的自主导航方法是当前磁测研究的热点[2，5－7]。磁测系统的姿态方程是非线性超越方程组，通常采用弦截法、抛物线法和牛顿迭代法等进行数值解算姿态参数。牛顿法是有效的方法，但其解算的收敛性和实时性与迭代初值相关。针对低旋转弹体的全弹道姿态解算，可以把前一解算点姿态作为当前解算迭代初值，这样能够把迭代过程引入收敛区，加快算法的收敛速度。对于高速旋转弹体，如采用这种方法，收敛缓慢甚至发散。因此，本文利用遗传算法在数值求解中能快速逼近最优解的特性，让遗传算法在姿态区间内对根进行快速搜索得到近似解，并以此近似解作为牛顿迭代法的迭代初值，然后采用牛顿法求取数值最优解，保证算法的收敛性与实时性。

1 磁测姿态解算方法

1.1 磁测姿态解算的基本公式

根据磁阻传感器姿态测量原理，捷联磁阻传感器测量值与导航系中地磁分量的关系为

式中：为地磁矢量在弹体坐标系中的分量为地磁矢量在导航坐标系中的分量。以地面发射坐标系为导航参考坐标系，弹体坐标系的原点O取在弹体质心，Ox轴与弹体纵轴重合，指向头部为正，Oy轴位于弹体纵向对称面内与Ox轴垂直，指向上为正，Oz轴垂直于Oxy平面，方向按右手直角坐标系确定。则导航坐标系与弹体坐标系的姿态矩阵Cbn为

式中：θ为俯仰角，ψ为偏航角，γ为横滚角。由式（1）整理后可得：

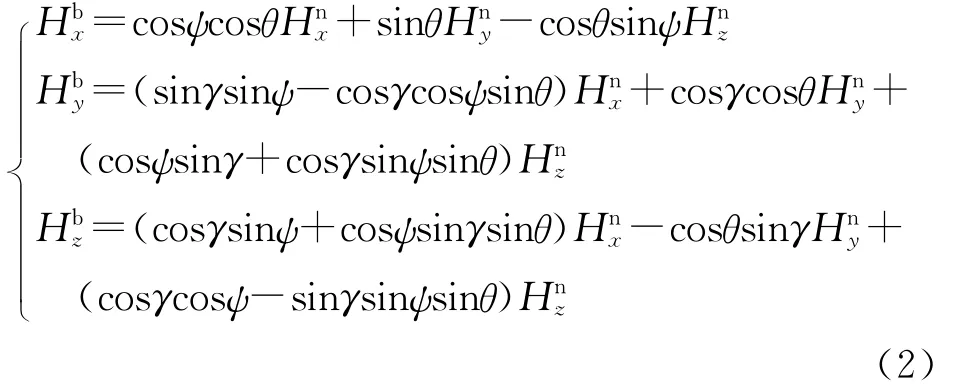
该非线性方程组是姿态解算的基本公式，在不考虑探测盲区的情况下，利用数值解算可以提取全弹道飞行姿态参数。

1.2 基于牛顿迭代法的姿态解算方法

牛顿法是解决非线性无约束最优化问题的方法，在给定合适的初值情况下，它能够快速收敛到方程的解，根据牛顿迭代法求解非线性方程的基本思想，首先将方程组（2）简写成如下形式：

对大多数炮射高速旋转弹，在标准气象条件下其距离散布远大于方向散布，偏航角变化很小。姿态解算时ψ，和均可视为已知量，通过解算方程组（2）可得到弹体姿态角θ和γ。假设X＊＝（θ＊γ＊）T为近似解，X0＝（θ0γ0）T为迭代初值。方程组（3）在近似解X＊处的一阶Taylor展开式为，则式（4）可简写为

若ATA可逆，式（5）存在最小二乘解为ΔX＝（ATA）－1ATB。此时姿态方程（5）的第一个近似解为X＊＝X0＋ΔX。迭代过程中根据max‖ΔX‖≤ε判断方程是否收敛，ε为迭代精度。若当次迭代的解不满足收敛条件，在进行下一次迭代前，需将当前近似解作为下一次迭代的初始值，重复迭代直到满足精度。因此，通过求解线性方程组（5），可以间接得到原非线性方程组（2）的近似解。

2 遗传－牛顿法的姿态优化算法

上述牛顿迭代法中，过程的收敛性与初始近似解X0的选取相关，初始点的选取只能在X＊的合适邻域内，但实际上很难检验所选X0是否靠近X＊。针对低旋转弹体的全弹道姿态解算，可以把前一解算点姿态作为当前解算迭代初值，这样能够把迭代过程引入收敛区，加快算法的收敛速度。但对于旋转速度达30 r/s的高速旋转弹体，这种方法收敛缓慢甚至发散。为了克服牛顿法的上述缺点，利用遗传算法在数值求解中能快速逼近最优解的特性，首先确定目标函数f（X）解的上下界，让遗传算法在尽量小的区间内对根进行搜索近似解，以该近似解作为牛顿法的迭代初值X0，以保证算法的收敛性[8]。

本文所述遗传－牛顿法的姿态优化算法步骤如下[9－10]。

①根据俯仰角的定义域[－90°，90°]，选定遗传算法的初始群体Ppop（s），s＝1，2，…，7。初始群体由7个染色体组成，染色体是俯仰角的8位二进制编码，分别为俯仰角－90°，－60°，－30°，0°，30°，60°，90°对应的二进制编码。

②对Ppop（s）初始群体中的每一个染色体分别计算其适应度函数fi，若fi趋于稳定，计算概率：

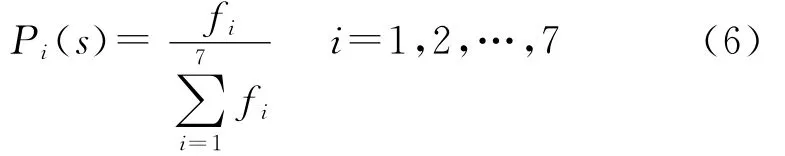
③以此概率分布从Ppop（s）中随机选出染色体用于构成新种群Pnewpop（s＋1）：Pnewpop（s＋1）＝｛Ppop（s）｜s＝1，2，…，7｝，设交叉概率Pc＝0.5，变异概率Pm＝0.01，通过交叉与变异操作形成一个新的种群Pnewpop（s＋1），重复上述计算操作（包括适应度函数与概率、交叉以及变异等），直到俯仰角的解算精度达到1°之内，并将此解作为应用牛顿法初始值θ0。

④横滚角的初值γ0求解方法与俯仰角基本相同，篇幅所限，不再列出详细解算过程，最后，以X0＝（θ0γ0）作为初始值，利用牛顿迭代法解算姿态方程的最优解。

3 算法仿真及误差分析

以某高速旋转弹作为仿真对象，本文采用六自由度刚体弹道方程，在标准气象条件下，利用 Matlab仿真计算得到全弹道姿态角数据。假定发射点所在地地理参数：东经105°24′，北纬38°01′，海拔800m，射向α＝42.25°，射角β＝42°，全弹道偏航角变化范围约为0.4°，俯仰角在42°～－59.6°之间变化，弹丸旋转平均转速约为40r/s。根据IGRF模型，仿真生成各轴磁传感器输出数据。

3.1 算法仿真

算法解算时，取原始姿态角数据中的偏航角作为每次迭代解算的偏航角初值，即假定偏航角为理论值，取初始俯仰角为射角42°，初始横滚角为0°，迭代精度设置为0.001°。用遗传－牛顿法解算全弹道飞行姿态，并与弹道方程所得的理想全弹道姿态进行了比较。姿态解算结果如图1、图2所示。

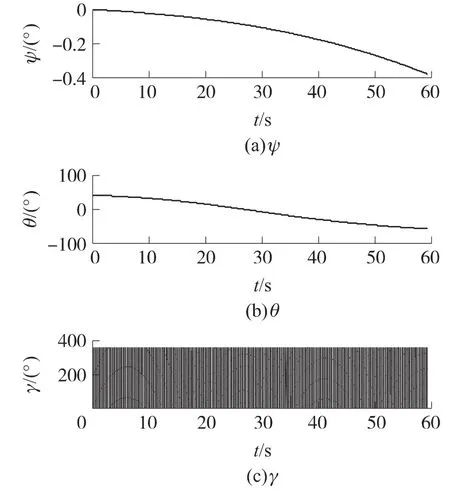
图1 姿态解算结果

图2 解算姿态角误差

在未知初始姿态情况下，初值X0的搜索过程必须遍历姿态角的整个姿态定义域，解算算法的精度取决于遍历过程中步长的设置，需要在精度与速度间做合适的选择，减小步长有利于提高姿态角的姿态解算精度，但也会导致遍历搜索速度变慢，从而影响算法的实时性。牛顿－遗传算法与常规遍历算法的解算精度、速度比较如表1所示，表中，St为搜索区间，h为步长，t为计算时间，M为进化代数，N为迭代次数，Δθ和Δγ分别为θ和γ姿态角的解算误差。

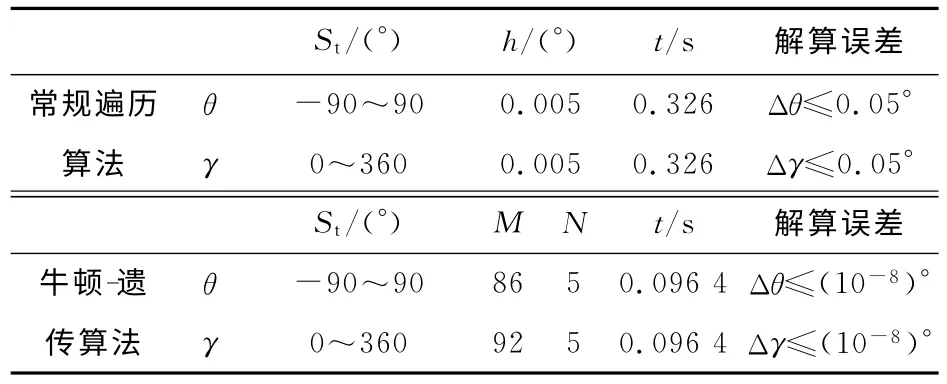
表1 牛顿－遗传算法与常规遍历算法的解算精度、速度比较

结果表明，如果偏航角与理论值一致，解算得到的俯仰角和横滚角误差非常小，在（10－8）°数量级，完全可以忽略不计。对比表1可知，牛顿－遗传算法相比常规遍历算法确实提高了算法实时性与解算精度。在实弹飞行环境下，可以通过增大步长，适当地牺牲姿态解算的精度来提高计算速度。

3.2 偏航误差对解算的影响

上述算法仿真时，偏航角假定已知，在没有其他辅助测量情况下，偏航角是无法确定的。在分析偏航误差对解算的影响时，假定全弹道无偏航，偏航角ψ＝0，其他仿真条件与3.1中相同，解算姿态角误差如图3所示。

图3 解算姿态角误差（偏航为零）

从图3中可以看出，假定偏航角不变，会造成偏航角误差，在解算俯仰角和横滚角时带来误差。偏航角误差约0.4°，俯仰角误差约0.15°，横滚角误差约0.4°。可见偏航角误差对俯仰角和横滚角的解算误差影响程度不同。

为进一步分析偏航误差对解算结果的影响，假设上述给定的偏航角在弹体飞行过程中分别改变了1°，5°和10°，其余仿真条件不变，由此解算姿态角误差曲线如图4所示。

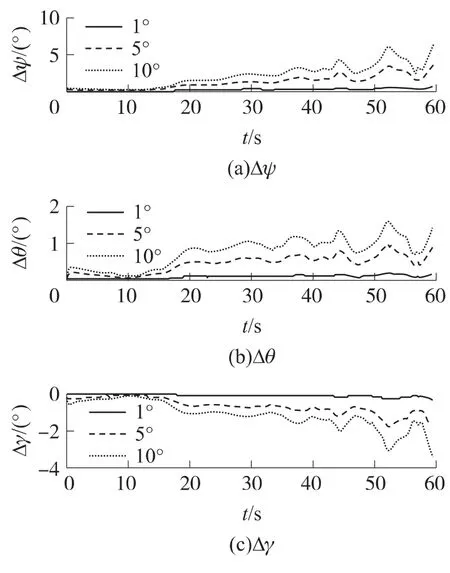
图4 偏航变化对解算精度的影响

从仿真结果中可以看出，当偏航角变化1°时，俯仰角误差约为0.2°，横滚角误差约为0.5°；当偏航角变化5°时，俯仰角误差约为1°，横滚角误差约为2°；当偏航角变化10°时，俯仰角误差约为2°，横滚角误差约为6°。实际上常规弹药在射程内偏航角变化10°的可能性很小，通常在1°～5°范围内。因此，即使恶劣环境下横滚角误差也不会超过2°，而环境条件较好的情况下俯仰角误差和横滚角误差分别低于0.2°和0.5°。数值计算表明，假定偏航角不变，解算得到的俯仰角和横滚角的精度能够满足测量要求，算法具有较高的解算精度。

3.3 磁测数据误差对解算的影响

三轴磁阻传感器存在的灵敏度误差、零偏误差、非正交误差和安装误差以及周围电磁干扰等均会造成磁测量数据不准确。为了分析磁测数据误差对解算的影响，仿真中假设三轴磁阻传感器存在10～500nT的随机测量误差，并设置偏航角与理论值一致，其余仿真条件与3.1中相同。图5为500nT磁测数据误差时的解算误差曲线。由仿真结果可知，磁测数据存在100nT随机测量误差时，俯仰角误差幅值小于0.3°，横滚角误差幅值小于0.5°；而最大偏差为500nT时，俯仰角误差幅值小于1.5°，滚转角的误差幅值最大也不超过3°。

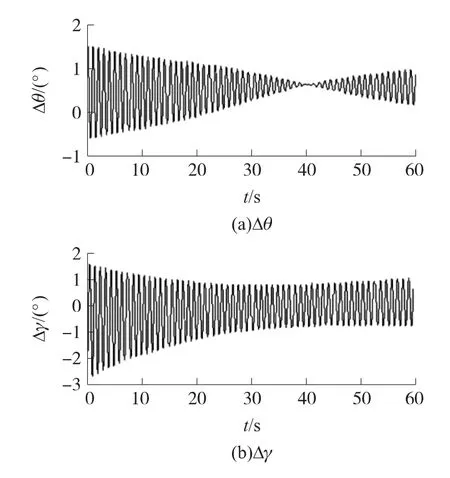
图5 磁测数据误差对解算精度的影响

此外，为分析初始地磁三分量数据的不准确对解算结果的影响，分别假设初始地磁三分量有100～1 000nT的误差（ΔH0），其余条件不变，仿真结果如图6所示。

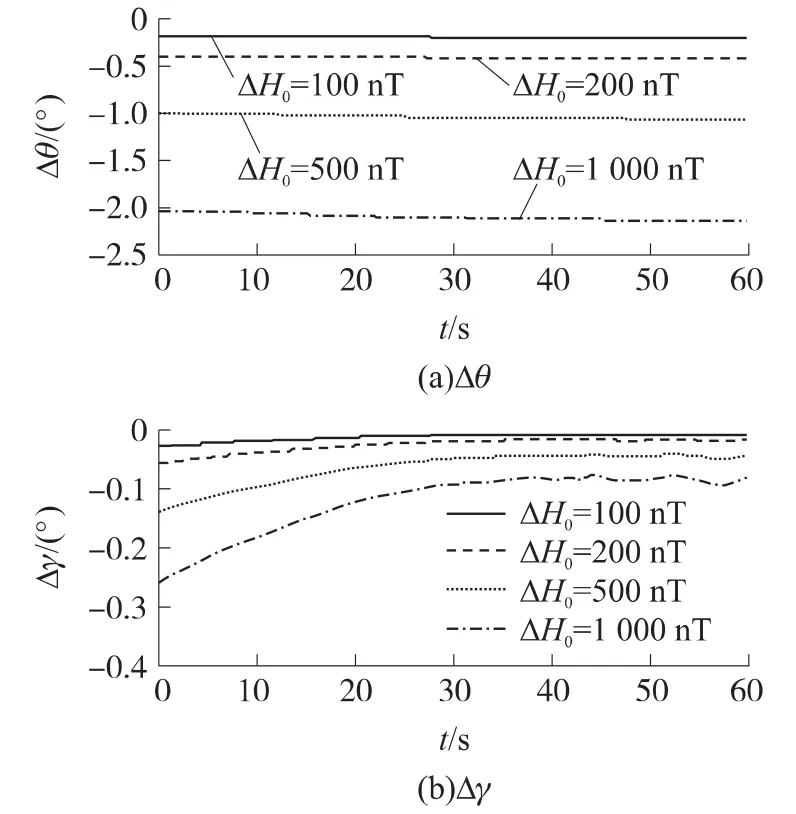
图6 初始地磁三分量不准确导致的姿态角误差

从结果来看，初始地磁三分量和磁阻传感器测量数据的变化对姿态角解算带来不同的误差影响，初始地磁三分量存在固定的常数误差，导致的姿态角误差呈单调变化；而磁测数据三轴分量存在固定的常数误差，这导致姿态角误差随弹丸旋转而产生周期性变化。这种情况表明，对数据进行后期处理时，可以通过频率的不同区别不同误差。

4 结束语

受常规弹药的高旋转、高冲击、小体积等恶劣应用环境的限制，利用捷联磁传感器测量高速旋转弹飞行姿态是一种有工程应用价值的测试方法。针对磁测姿态方程是非线性超越方程组，磁测解算中牛顿迭代法存在收敛缓慢甚至发散的问题。本文利用遗传算法在姿态角定义域内对根进行快速搜索得到近似解，并以此近似解作为牛顿迭代法的迭代初值，保证算法的收敛与实时性。以某高速旋转弹为算例，进行了姿态角解算，分别从给定姿态角误差、初始固定参数误差和磁测数据误差三个方面进行了算法误差影响分析，数值仿真结果表明，牛顿－遗传算法确实能够解决算法收敛缓慢与发散的问题，且提高了算法实时性与解算精度，验证了算法的可行性，但由于算法的仿真计算是建立在普通PC机平台的离线数据处理方式上，特别是由于弹上计算机性能的限制，算法在实弹飞行环境下必须综合考虑姿态计算的速度与精度平衡。

[1]高峰，张合.基于基准角和补偿角的常规弹药滚转角磁探测算法研究[J].探测与控制学报，2008，30（5）：11－15.GAO Feng，ZHANG He.Algorithm of roll angle determination of conventional ammunitions based on benchmark angle and compensation angle[J].Journal of Detection and Control，2008，30（5）：11－15.（in Chinese）

[2]史金光，韩艳，刘世平，等.制导炮弹飞行姿态角的一种组合测量方法[J].弹道学报，2011，23（3）：37－38.SHI Jin－guang，HAN Yan，LIU Shi－ping，et al.An approach of combination measurement for flight attitude angles of guided projectile[J].Journal of Ballistics，2011，23（3）：37－38.（in Chinese）

[3]鲍亚琪，陈国光，吴坤，等.基于磁强计和 MEMS陀螺的弹箭全姿态探测[J].兵工学报，2008，29（10）：1 227－1 231.BAO Ya－qi，CHEN Guo－guang，WU Kun，et al.Research on attitude determination using magnetometers and MEMS inertial sensors[J].Acta Armamentarii，2008，29（10）：1 227－1 231.（in Chinese）

[4]苟秋雄，刘明喜，李虎军.基于磁阻传感器的末制导迫击炮弹滚转姿态初始对准技术研究[J].弹箭与制导学报，2008，28（3）：45－47.GOU Qiu－xiong，LIU Ming－xi，LI Hu－jun.Research of terminal guide mortar bomb roller attitude initial alignment technique based on magnetic resistance sensor[J].Journal of Projectiles，Rockets，Missiles and Guidance，2008，28（3）：45－47.（in Chinese）

[5]马国梁，李岩，葛敬飞.磁阻传感器测量旋转弹滚转姿态的原理分析[J].弹道学报，2012，24（1）：32－36.MA Guo－liang，LI Yan，GE Jing－fei.Principle analysis for roll attitude spinning projectile using magnetic measurement of resistance sensor[J].Journal of Ballistics，2012，24（1）：32－36.（in Chinese）

[6]史连艳，张自宾，宋文渊.基于 MR/GPS的弹体姿态解算方法研究[J].系统仿真学报，2010，22（12）：2 948－2 951.SHI Lian－yan，ZHANG Zi－bin，SONG Wen－yuan.Study of rocket body attitude solving method based on MR/GPS[J].Journal of System Simulation，2010，22（12）：2 948－2 951.（in Chinese）

[7]李玎，卜雄洙.基于非正交磁传感器组合的旋转弹体横滚角测试[J].兵工学报，2010，31（10）：1 316－1 321.LI Ding，BU Xiong－zhu.Roll angle measurement of spinning projectile based on non－orthogonal magnetic sensors[J].Acta Armamentarii，2010，31（10）：1 316－1 321.（in Chinese）

[8]钱伟行.捷联惯导与组合导航系统高精度初始对准技术研究[D].南京：南京航空航天大学，2010.QIAN Wei－xing.Research on high－precision initial alignment of strapdown inertial and integrated navigation system[D].Nanjing：University of Aeronautics and Astronautics，2010.（in Chinese）

[9]HOLLAND J H.Adaptation in natural and artificial systems：an introductory analysis with applications to biology，control，and artificial intelligence[M].Ann Arbor：University of Michigan，1975.

[10]DORIGO M，MANIEZZO V，COLORNI A.Ant system：optimization by a colony of cooperative agents[J].IEEE Transactions on System，Man，and Cybernetics，1996，26（1）：29－41.