基于MCMC 的MTBF 值区间估计方法研究
孟庆东,杨 珍
(佛山市南海区技师学院,广东 528237)
0 引言
对机电产品进行可靠性分析最基本的工作是要确定其寿命分布参数。机电产品寿命服从两参数Weibull 分布,其分布参数的贝叶斯估计需要对后验分布进行二重积分。根据贝叶斯公式,在求解可靠性特征量MTBF 值区间估计时,需要进行内积分限为函数的二重积分。在进行积分时,由于Bayes 后验分布复杂且内积分限为函数,数值积分方法失效[1-3]。
利用Bayes 理论进行统计推断,需要积分运算。对于两参数Weibull 分布,需要对Bayes 后验分布进行二重积分。一般有两种方法进行积分运算,即数值积分与Monte Carlo 积分。
运用数值积分计算时会遇到一些问题。当被积函数较复杂时,将导致计算精度降低。同时,积分区间的大小也会直接影响计算结果,使得Bayes 后验计算出现不稳定的趋势。对于多重积分,因为每个外层积分都取决于内层积分在一组点上的取值,所以会出现误差的累积。
Monte Carlo 积分从目标分布中抽样模拟,利用随机抽样所得点进行统计推断,避免了数值积分中的求积节点计算与系统网格的划分,使得积分计算的效率与可操作性显著提高。但是,在Bayes 推断中,运用Monte Carlo 方法是有困难的,具体表现在Bayes 后验分布多为复杂、高维非标准的分布。当目标密度函数易于抽样时,可以利用Monte Carlo 方法产生近似样本,并利用样本的函数值计算Bayes 后验期望估计。当目标密度函数难以抽样时,可以利用MCMC 方法思想直接构造出Bayes 后验分布π(m,η|T)的马尔科夫链,基于所得样本可以进行各种统计推断[4-6]。
1 MCMC 方法
MCMC 方法通过建立一个以后验分布π(x)为平稳分布的马尔科夫链,对π(x)进行抽样,然后根据所得样本进行统计推断[7]。如通过抽样得到π(x)的样本X(1),…,X(n),则:
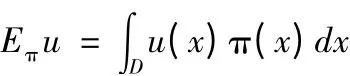
其中D 为状态空间,于是可得估计:
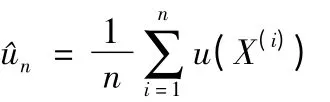
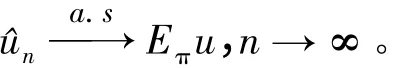
如果X(1),…,X(n)是平稳分布为π(x)的马尔科夫过程的样本时,上式也成立。
为了构造马尔科夫链,设给定状态Xt条件下,下一步状态为Xt+1。则任意选择一个不可约转移概率q(* ,* )以及一个函数α(* ,* ),定义p(x,y)=q(x,y)α(x,y),则p(x,y)为马氏链一个转移核。如果链在时刻t 处于状态x,即X(t)= x,首先由q(* | x)产生一个潜在的转移x →y,然后根据概率α(x,y)决定是否转移。可以从Unif(0,1)中抽一个随机数u,则:
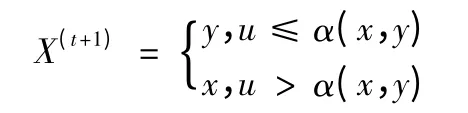
通常,称q(* ,* )为建议分布。
为使后验分布π(x)成为平稳分布,在有q(* ,* )后,应选择一个α(* ,* )使相应的p(x,y)以π(x)为其马氏链平稳分布,可以选择:
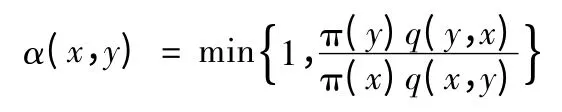
此时,可以证明产生的马尔科夫链是可逆的,满足平稳方程,即: π(x)q(x,y)= π(y)q(y,x)
2 Weibull 分布下MTBF 值区间估计
2.1 先验分布为伽马- 逆伽马分布的MTBF 值区间
选取均匀分布分布为建议分布,则:
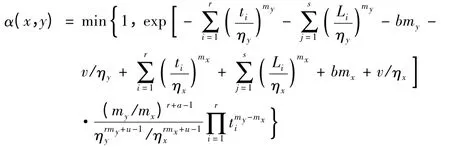
其中,α(x,y)为Metropolis-Hastings 比率,my和ηy是在一步迭代中,从建议分布中抽取的建议值,mx和ηx是一步迭代的初始值。迭代过程如下:
①θ = (m,η)= (θ(t-1)0,θ(t-1)1);
②从建议分布Unif(-0.5,0.5)中产生候选点;θ'
③令θ″ = θ + θ',即让建议值随机游动一个距离;
④根据上式计算接受概率α(θ,θ″);
⑤以概率α(θ,θ″)接受θ″ = θ(t),否则令θ =θ(t)。
以某机电新产品运行时间为现场样本,用上述方法进行计算,得到结果如表1 所示。
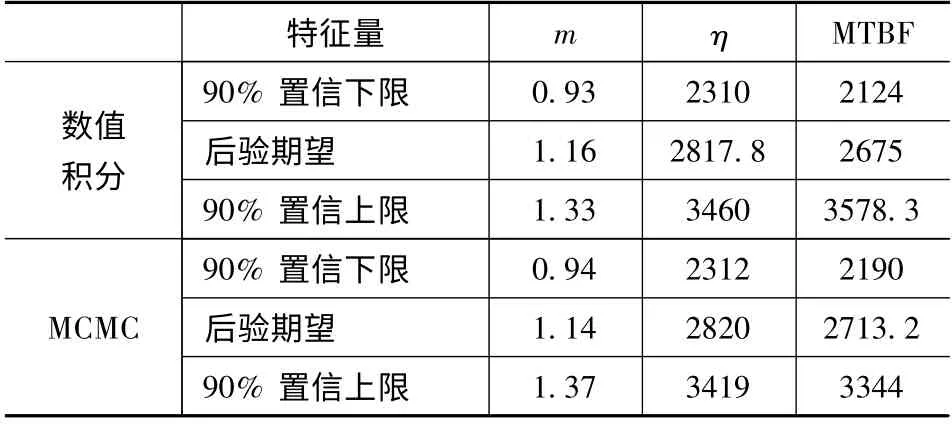
表1 MCMC 方法计算结果
图1 和图2 分别是参数m、η 以及MTBF 值的全部迭代轨迹和后验分布的密度直方图。

图1 参数m 和η 及MTBF 值迭代轨迹图

图2 参数m 和η 及MTBF 值的后验密度直方图
由于计算可靠性特征量MTBF 值区间估计时,数值积分方法失效,依据工程经验用参数点估计的区间估计端点来近似MTBF 值的置信区间。但是这种方法存在一定问题,一是求得的置信区间精度不高,有扩大的趋势;二是近似方法并没有可靠的理论支撑。通过表1 的计算结果,可以看出MCMC 方法解决了上述问题,使得可靠性评估在质量与效率上都得到提高。
2.2 先验分布为二元正态分布的MTBF 值区间估计
先验分布为二元正态分布时,计算结果如表2 所示。
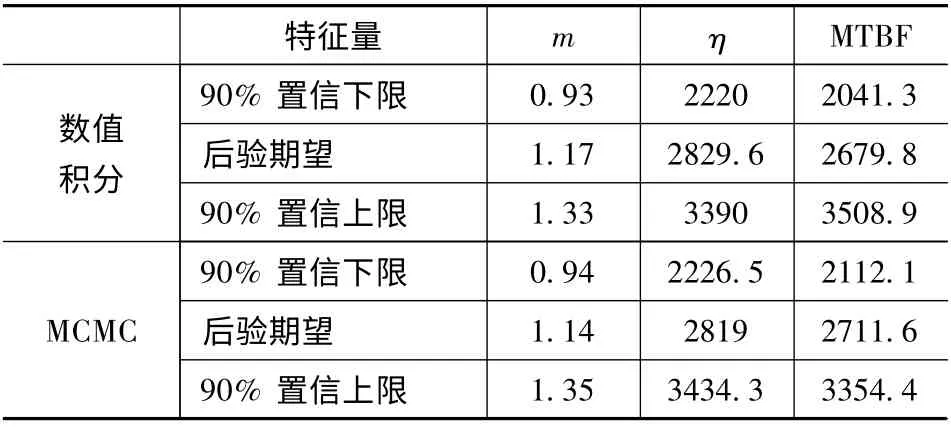
表2 MCMC 方法计算结果
图3 和图4 分别是参数m、η 以及MTBF 值的全部迭代轨迹和后验分布的密度直方图。
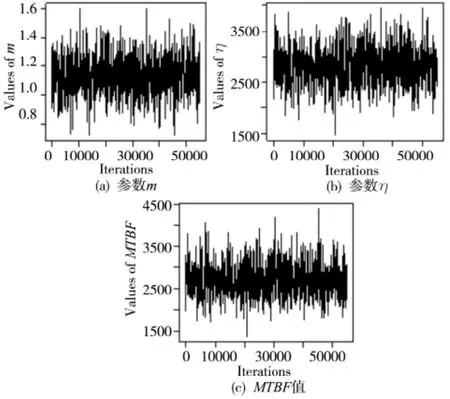
图3 参数m 和η 及MTBF 值的迭代轨迹图
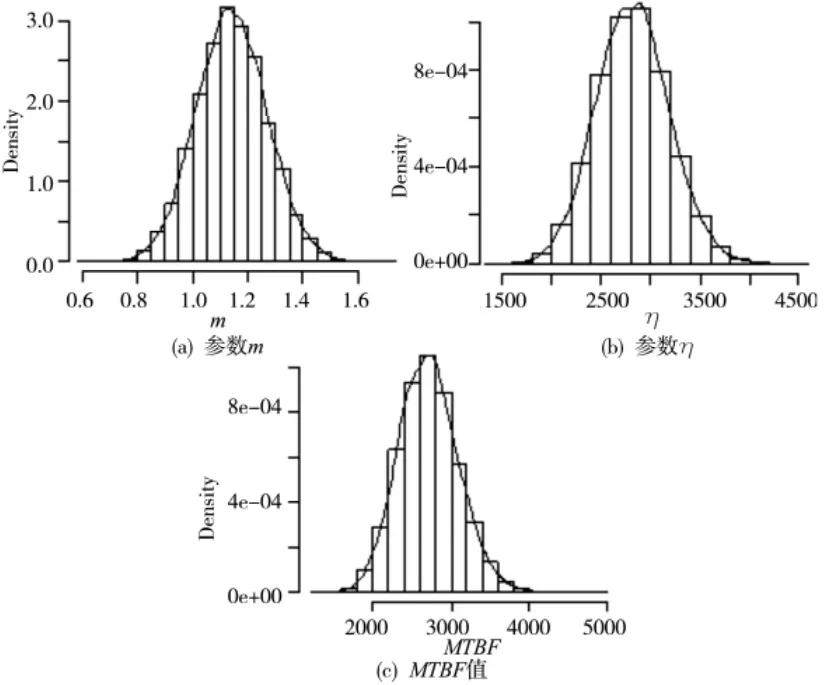
图4 参数m 和η 及MTBF 值的后验密度直方图
3 结论
通过MCMC 构建马尔科夫链,使Bayes 后验计算运用的数值积分方法转化成从简单的分布中抽样并推断。基于抽样所得分布参数样本,MTBF 值、可靠度、失效率等各种可靠性特征量的求解都可以有效实施,不再受数值积分的限制,提高了模型计算的稳定性、可操作性与适应性。MCMC 方法解决了数值积分问题带来的不便,有利于贝叶斯理论在可靠性评估中的推广。
[1]林静. 基于MCMC 的贝叶斯生存分析理论及其在可靠性评估中的应用[D]. 南京:南京理工大学,2008.
[2]李斌全,戴怡. 基于马氏链蒙特卡洛方法的数控系统可靠性评估[J]. 组合机床与自动化加工技术,2011(10):69-71.
[3]潘海涛,温小霓. 基于MCMC 方法的GARCH 模型参数估计[J]. 统计与信息论坛,2009,24(4):12-16.
[4]曹小群,宋君强,张卫民,等. 基于MCMC 方法的Lorenz混沌系统的参数估计[J]. 国防科技大学学报,2010,32(2):68-72,145.
[5]李凌,徐伟. 基于MCMC 方法的继电器加速寿命试验分析[J]. 低压电器,2010(2):13-16,35.
[6]王进玲,曾声奎,马纪明,等. 混合变量系统基于MCMC的自适应重要抽样法[J]. 宇航学报,2012,33(1):94-101.
[7]黎光明,张敏强. 先验信息对MCMC 方法估计概化理论方差分量变异量的影响[J]. 统计与决策,2012(7):27-30.

