基于启发式算法与仿真分析的混合流水线平衡优化*

查 靓，田 行

(三峡大学 机械与材料学院，湖北 宜昌 443002)

0 引言

混合流水线是指在不降低流水线效率的前提下，在一条流水线上实现具有相似特征的多个产品或者是一个产品系列的不同品种的混合生产，与单一产品流水线相比，能够在保持较低库存水平的情况下更加柔性的应对顾客个性化和多样化的需求。混合流水线平衡是混合流水线优化设计的重要问题之一。这是因为混合流水线平衡有利于:(1)消除生产瓶颈，减少架线成本，提高生产效率。(2)提升员工士气，稳定产品质量。(3)加快物流周转，缩短生产周期，减少或消除物料及半成品周转场所。

混合产品流水线平衡远比单一产品流水线平衡复杂，现有研究多采用遗传算法、蚁群算法、粒子群算法等智能算法进行求解。张则强等［1］提出了一种带信息素总合规则和混合搜索机制的蚁群算法进行求解。徐炜达和肖田元［2］研究了带有跨工位操作，且作业完成时间为随机量的混合装配线平衡问题，结合随机模拟和遗传算法设计了混合遗传算法进行求解。Reakook Huang 和Hiroshi Katayama［3］设计了两阶段遗传算法求解多目标U 型混合流水线平衡问题。凌文曙［4］利用遗传算法解决了某车桥混合装配线平衡问题。但是，智能算法计算复杂，耗时较长，基于规则的启发式算法计算简单快捷［5］，容易为生产实践者理解和掌握，在单一产品流水线平衡实际应用较多，但对混合流水线平衡优化精度不高，特别是对不同产品在每个工作站的作业时间均衡效果不佳。因此，本文提出一种将启发式算法和仿真分析相结合的方法，首先将多产品的作业优先次序图转化为单一产品综合作业优先次序图，然后利用基于规则的启发式算法求得初始平衡方案，接着根据混合流水线运行特点建立仿真模型，通过仿真分析，辨识存在的问题并进行改进，从而得到最终优化平衡方案。

1 混合流水线平衡问题的描述

根据流水线上加工产品品种的多少，流水线平衡问题可分为单一产品、多产品和混合产品流水线平衡问题。其中，单一产品流水线上只生产一种产品，多产品流水线上以一定的批量轮番进行多种产品的生产，例如生产100 个产品A 后再生产100 个产品B，混合品种流水线上是以一个最小比例集轮番进行多种产品的混合生产，例如以(A，B)为最小比例集重复生产100 次。

混合流水线平衡问题是指:给定加工多个产品的作业优先次序图，包括作业集合、作业加工时间以及作业间的优先次序关系等信息，将作业组合分配到工作站，要求每个作业都被分派且只能被分派到一个工作站，每个工作站的作业时间不大于节拍，满足作业间的优先次序要求，并使得某些指标达到优化。

2 混合流水线平衡问题向单一产品流水线平衡问题转化

混合流水线由于需要完成多个产品的加工，因此对应了多个产品的作业优先次序图，为了能利用单一产品流水线平衡方法来求解，第一步应该是如何将多个作业优先次序转化为一个作业优先次序图。

令第p 个产品的作业优先次序图用有向图Gp =(Tp，Pp，tp)表示。则PN 种产品的综合作业优先次序图为)G = ()T，)P，)t)。其中:

= {(i，j)| )Ti必须在)Tj完工后才能开始}

由于Tp⊆)T，因此定义δpi表示Tp中是否包括作业i(i ∈)T)，如果包括δpi= 1，否则δpi= 0。计划期内第p 个产品的需求数量为dp，总产品数为)d，则计算出每个作业元素的加权平均作业时间为:

3 启发式算法

在一个有向网络图中，从起点开始，按照作业顺序，连续不断地到达终点的一条通路称为一条网络路线。其中，完成每一作业需要时间最长的路线称为关键路线，关键路径上的作业的松弛时间为0，松弛时间= 作业最迟开始时间－作业最早开始时间－作业时间。正因为关键路径决定了完成所有作业需要的最长作业时间，因此尽可能早的开始执行关键路径上的作业越有利于减少所需要的总工作站数。关键路径可以利用运筹学中的网络前向分析和后向分析，然后根据松弛时间为0 计算得到［6］。

双向启发式算法的特点是［7］，同时从第一个工作站和最后一个工作站开始，从前向后和从后向前同时试分配可行的候选作业到前向工作站和后向工作站，在分配过程中优先分配关键路径上的作业，如果试分配的前向工作站的空闲时间小于试分配的后向工作站的空闲时间，说明前向工作站的试分配方案优于后向的，接受前向工作站试分配方案，放弃后向的，否则接受后向工作站试分配方案，放弃前向的。接着进行下一工作站的试分配，直到所有作业均被分配到工作站。

计算步骤如下:

第一步:计算关键路径作业集合Scp，非关键路径作业集合Scp= S－Scp。

第二步:初始化。所有作业均未分配到工作站Su= S，Sa= φ，同时从第一个工作站和最后一个工作站开始分配作业，因此令首工作站为当前前向工作站，末工作站为当前后向工作站，即i = 1，j = 1。

第三步:创建两个临时前向工作站和后向工作站作业集合，初始为空，FSi= BSj= φ。

第四步:试分配。筛选可行的候选作业集合，即未分配的，且不存在未分配的前序作业可分配到当前前向工作站i，如果候选作业集合中存在关键路径上的作业，首先分配到临时前向工作站FSi，然后按照最长作业时间等规则依序分配候选作业集合里的作业直到FSi的总作业时间超过节拍C 为止。同理，如果存在未分配的且不存在未分配的后序作业可分配到当前后向工作站j，如果候选作业集合中存在关键路径上的作业，首先分配到临时后向工作站BSj，然后按照最长作业时间等规则依序分配候选作业集合里的作业直到BSj的总作业时间超过节拍C 为止。

第五步:确定分配方案。对于临时工作站集合FSi和BSj，如果FSi的空闲时间小于BSj的空闲时间，即Wf ≤Wb，说明当前前向工作站i 的临时分配方案优于后向工作站j 的，因此接受FSi的分配方案成为固定分配方案，放弃BSj，即i = i +1，Sa= Sa∪FSi，Sa= Su－FSi，FSi= BSj= φ。如果Wf ＞Wb，说明后向工作站j 的临时分配方案优于前向工作站i 的，接受BSj的分配方案成为固定分配方案，放弃FSi，即j = j +1，Sa= Sa∪BSj，Sa= Su－BSj，FSi= BSj= φ。

第六步:如果Su= φ 说明所有作业都已分配到工作站，程序结束，输出分配方案，否则，返回第四步继续执行。

算法流程图如图1 所示。

图1 启发式算法的计算流程图

4 评价指标

4.1 单一产品流水线平衡指标

单一产品流水线平衡效果常采用生产线平衡效率p 作为评价指标，如下式:

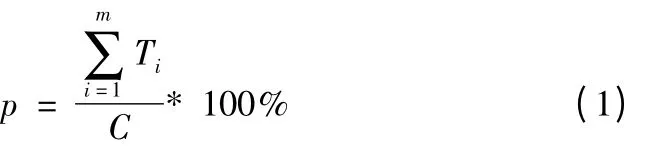
其中m 代表工作站数，Ti代表工作站i 的平均作业时间，C 为节拍。p 值越大说明平衡性越好，生产效率越高。对于p 值，文献［8］给出了推荐的评定标准，如表1 所示。

表1 单一产品流水线平衡性评价标准

4.2 混合流水线平衡指标

由于混合流水线上加工的是多个产品，在一个周期的不同阶段每个工作站实际加工的产品会发生变化，每个工作站的实际作业时间也随之发生变化，尽管按照启发式方法得到的初始方法平衡效率p 值高，但不同阶段的工作站实际作业时间仍存在不平衡现象，甚至出现超过节拍的现象。

通常采用两种方法解决:一是调整生产节拍C，使流水线节拍大于或等于最长工作站作业时间，这种方式降低了生产速度，无法满足客户需求;二是保持节拍C 不变，采取补救措施(如设置线外工作站修补)完成，采取这种方式时，每个工作站作业时间超过节拍的程度也称超负荷量对生产效率影响大，总的超负荷量越大，线外补救的工作就越多，需要的赶工成本越大。此外，工作站负荷不均衡，有的工作站作业时间很长，有的工作站作业时间很短，也会对产品质量和员工士气产生很大影响。

因此，最长作业时间、总的超负荷量以及负荷均衡指数对于混合流水线的最优化设计至关重要，本文选择这三个指标作为混合流水线平衡效果的评价指标。

总的超负荷量的计算如式(2)所示。

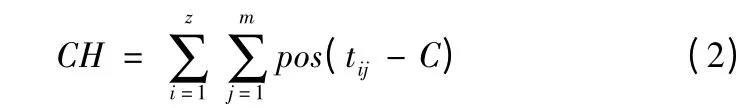
如果a ≥0 则pos(a)= a;否则pos(a)= 0。

负荷均衡指数的计算如式(3)所示。

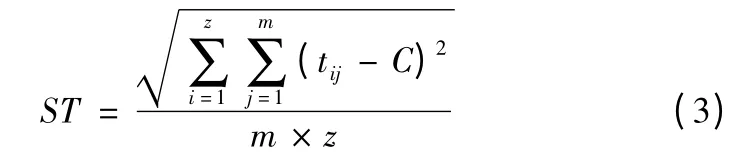
利用平均作业时间和启发式算法得到的初始平衡方案无法保证这三个指标的最优性，因此需要根据混合流水线特点建立仿真模型，进而提出改善方案。

下面通过一个案例来说明和验证本文所提方法的有效性。

5 案例应用

5.1 案例背景介绍

某客车空调生产企业原先客户少，生产品种数少，随着技术能力的增强，为扩大利润，开发了一些新的客户，针对客户需求研发了几个系列的新产品，这些新产品利润高，品种多，但单一品种客户需求数量少，为了节省架线成本和运行成本，受精益生产思想的影响，公司拟针对系列产品采用混合装配流水线进行生产，因此需要设计一条新的混合流水线。

选定A(内置式)、B(全顶置式)、C(半顶置式)三种产品，根据市场调研与预测，每个月三种产品的需求分别为200、200 和400 台，该企业每周工作6 天(一个月26 个工作日)，每日工作8 小时，需求节拍CT 为:

根据需求节拍CT 的值，考虑一定的宽放系数混合流水线的生产节拍设计为15 分钟。

5.2 综合作业优先次序图

三种产品的作业优先次序图如图2、3、4 所示。其中，作业间的优先次序是根据产品装配工艺的要求绘制的，每个作业的作业时间是根据模特法，并考虑一定的评比系数和宽放系数后预订的标准作业时间。

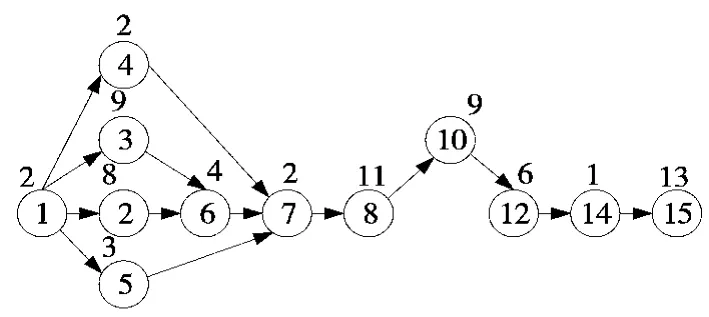
图2 产品A 的作业优先次序图

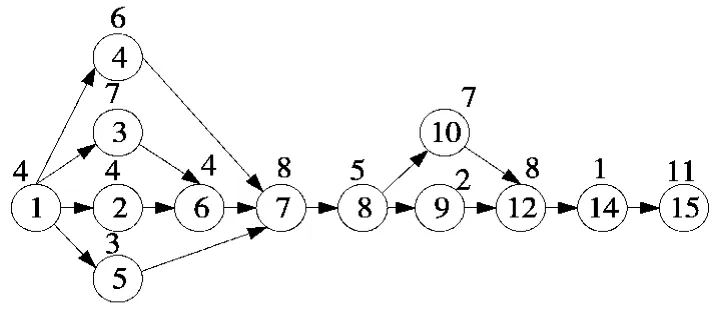
图3 产品B 的作业优先次序图

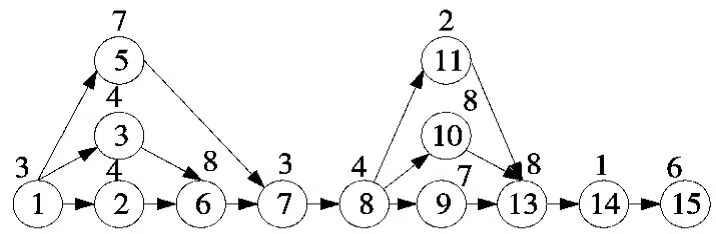
图4 产品C 的作业优先次序图

根据每个月三种产品的需求得到综合产品作业优先次序图如图5 所示。

图5 综合作业优先次序图

5.3 求解单一产品流水线平衡问题

按照基于关键路径的双向启发式算法，首先计算关键路径作业集合为Scp= {1，3，6，7，8，10，12，14，15}，然后按照图1 所示的流程将作业分配到工作站的分配过程如下表2 所示。得到的作业分配方案如表3 所示。平衡有效性指标

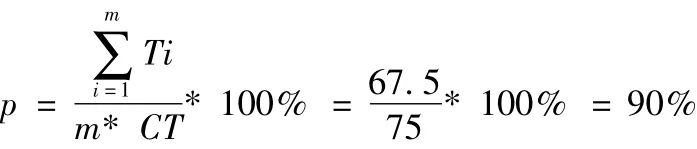
根据表1 的评价标准，p ≥90% 可以认定该单一产品流水线平衡方案是优的。

表3 初始作业分配方案

5.4 仿真分析

一个月内三种产品的需求为200、200 和400，需求比例为1:1:2，为了确保零件消耗的均衡性，采用比例倒数法确定在一个循环内三种产品投放的顺序为CBAC，据此建立仿真模型。仿真结果表明，在一个周期的四个阶段内五个工作站中出现的产品及工作站作业时间如表4 所示，工作站实际负荷如图6 所示。

表4 改善前一个周期内工作站加工产品及作业时间

图6 改善前工作站负荷

最长工作站作业时间为20，远超过节拍15 的要求。工作站1 在第3 阶段，工作站4 在第3、4 阶段，工作站5 在第2、3 阶段，作业时间较长，成为瓶颈工作站，超出节拍，而工作站4 在第一阶段的作业时间只有7，工作站5 在第4 阶段的作业时间只有8，远小于节拍，存在空闲时间。总的超负荷量为4000，负荷均衡指数为0.95。

由此可以看出，虽然初始方案针对以加权平均作业时间为参数的单一产品流水线而言平衡效率为优，但考虑了每个产品实际的作业时间后的混合流水线上，由于排序方案的不同使得每个工作站出现的产品不同，使得工作站作业时间不同，从而出现不平衡现象，甚至超出节拍需求，在有些时间段内个别工作站无法完成作业，需要在工作站上增加额外的活动工人来完成超出的负荷，才能使流水线正常运行。因此有必要寻求更好的平衡方案较少超负荷量水平，从而减少线外工作站的修补工作量，提高生产效率，提高质量。

5.5 优化方案

工作站1 对A 的作业时间为19 分钟，超负荷明显，而工作站2 中对A 产品没有超负荷现象，所以考虑对工作站1 进行拆分，与工作站2 中作业进行重新分配;工作站4 与工作站5 的超负荷现象更加明显，C 产品在工作站4 中作业时间超过节拍，而在工作站5 的作业时间只有8 分钟，远小于节拍;A、B 产品在工作站5 中作业时间超过节拍，而在工作站4的作业时间较小，所以考虑对工作站4、5 进行拆分，对其中的作业重新分配。改进后的平衡方案如表5 所示。

针对改进的平衡方案，加入排序方案后，产品以投入顺序CBAC 循环进入生产线，重新构建仿真模型，仿真结果表明在一个周期的四个阶段内五个工作站中出现的产品及工作站作业时间如表6 所示，工作站实际负荷如图7 所示。

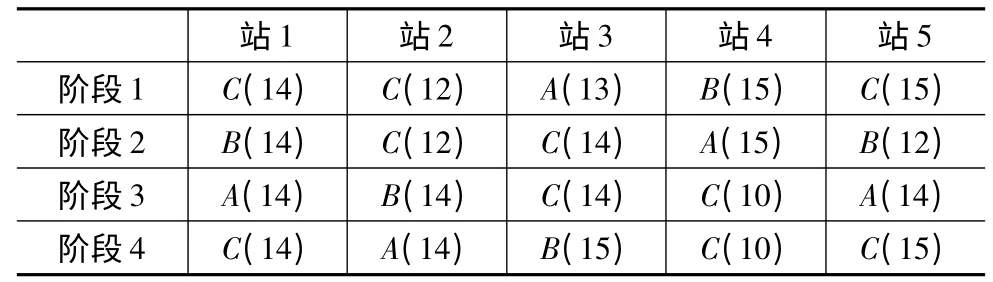
表6 改善后一个周期内工作站加工产品及作业时间

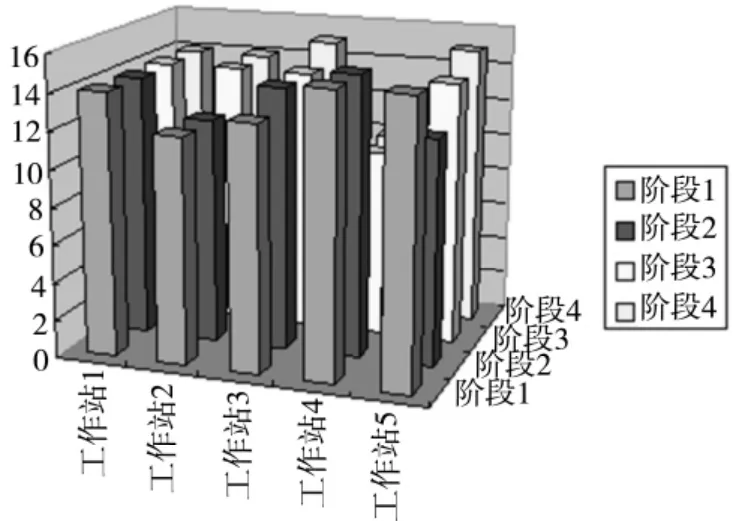
图7 改善后工作站负荷图

改善后最长工作站作业时间为15，满足节拍15的要求，不存在工作站作业时间超过节拍的情况，CH= 0，负荷均衡指数为0.47，大大小于初始方案，改进后的平衡效果优。

6 结束语

混合流水线的平衡过程是实现劳动生产率、设备利用率和满足市场需求三者之间平衡的过程，混合流水线平衡效果直接影响到流水线的生产效率。本文针对混合流水线设计与运行的特点，采用启发式算法和仿真分析相结合的方法求解混合流水线平衡问题，通过对某客车空调生产企业三种产品混流生产线的设计发现，经过平衡优化后，能够减少最长工作站作业时间，避免工作站实际负荷超节拍的情况，大大减少工作站间负荷不均衡，达到提高生产效率，降低生产成本，提升员工士气，稳定产品质量等目的。

［1］张则强，程文明，钟斌，等. 混合品种装配线平衡问题的一种混合搜索机制的蚁群算法［J］. 机械工程学报，2009，45(5):95－101.

［2］徐炜达，肖田元. 可跨工位操作的随机混流装配线平衡问题研究［J］. 系统仿真学报，2009，21(18):5896－5901.

［3］Reakook Hwang，Hiroshi Katayama. A multi-decision genetic approach for workload balancing of mixed-model U-shaped assembly line systems［J］. International Journal of Production Research. 2009，47(14):3797－3822.

［4］凌文曙. 基于遗传算法的混流装配线工作站平衡［J］.合肥工业大学学报，2008，31(8):1287－1291.

［5］Armin Scholl，Christian Becker. State-of-the-art exact and heuristic solution procedures for simple assembly line balancing［J］. European Journal of Operational Research，2006，168(3):666－693.

［6］李荣钧. 运筹学导论［M］. 北京:科学出版社，2009.

［7］Din-Horng Yeh，Hsiu-Hsueh Kao. A new bidirectional heuristic for the assembly line balancing problem［J］. Computers ＆ Industrial Engineering，2009，57(4):1155－1160.

［8］吴隆，余海明，吴媛媛. 基于Lingo 的汽车装配线建模与平衡优化［J］. 工业工程与管理，2008(6):74－77.