基于改进粒子群算法的无刷直流电机控制研究*
付光杰,杨帛润,高俊莹
(东北石油大学 电气信息工程学院,黑龙江 大庆 163318)
0 引言
随着电力电子技术及新型永磁材料的发展,无刷直流电机(Brushless DC Motor,以下简称BLDC)迅速成熟发展起来成为一种新型电机[1]。无刷直流电机既具有体积小、效率高和维修方便等特点,又具有宽阔而平滑的优良调速性能,因此在各个领域得到广泛应用。随着驱动系统的快速发展和无刷直流电机应用领域的不断拓展,要求控制系统日益趋于智能化和数字化,为更多复杂的控制技术提供实现的平台,达到系统设计周期短、成本低、易于改进和维护等目的。
PID 控制是一种技术最为成熟、应用最为广泛的控制算法,具有结构简单、参数调整方便、稳定性好等优点[2-3]。但随着工程系统的日益复杂化,传统的PID 控制器满足不了对控制要求的精确化,尤其对不确定性的、时变的、多变量关联的非线性复杂系统,传统PID 控制器的适应性慢、鲁棒性弱和协调性不好等缺点逐渐显露出来,所以近些年应用智能算法优化PID 控制器在工程控制中逐渐被重视起来。
1 无刷直流电机的控制模型
图1 为无刷电机控制系统结构图,本文主要目的是调速,因此调速系统采用双闭环控制:速度环采用PSO 算法优化的速度控制器;电流环采用电流滞环控制器。转速环作为主环在外侧,电流环作为副环在内侧,可以有效地抑制外界扰动对转速的影响,进而获得良好的静、动态性能[4]。
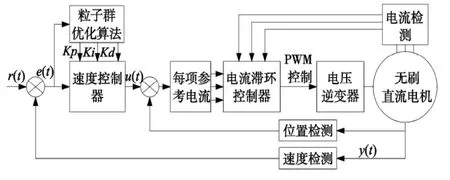
图1 无刷电机控制系统结构图
图1 中r(t)—给定电机转速值;y(t)—反馈的转速值;e(t)—转速偏差;u(t)—PID 控制器输出的电压控制量。
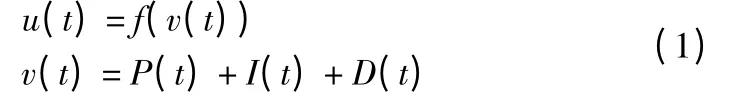
其中:

在上式中dI/dt 的作用是防止积分值越界;Tt是一个时间常量。Kp、Ki、Kd是利用PSO 算法优化的系数;C 通常取值为10。
在PID 控制器中比例环节的主要作用是能够快速地对偏差做出反应,使得控制量向减少偏差的方向发展。积分环节主要作用是通过消除静差来提高系统的抗干扰性,但过大的积分系数会导致滞后现象,使得系统响应速度变慢、超调量变大,甚至可能产生震荡[5]。微分环节调节主要是反映偏差的变化速率,对误差的变化有预判的作用,阻止误差向放大的趋势发展,提前向系统中引入一个有效的修正信号防止偏差信号值趋于过大,减少了调节时间,从而改善了系统的动态特性。但微分环节的抗干扰能力差,对输入的噪声量非常敏感,所以要提前对输入信号进行滤波。
2 粒子群算法PID 控制器的参数优化
2.1 粒子群算法
粒子群优化算法(PSO)是于1995 年Kennedy 和Eberhart 等提出,灵感来源于鸟群在寻觅时的行为,是一种群体智能优化算法,并发展成为一种基于迭代的有效优化工具[6]。
在粒子群算法中,每个待优化问题的潜在解被当做成d 维搜索空间上的一个点,把每一个点称为“粒子”,总共有n 个粒子组成一个群体为S ={x1,x2,…,xn}。被优化问题目标函数确定的适应值(Fitness Value)决定所有粒子性能的优劣程度,还有一个速度决定每个粒子的飞翔方向和速率的大小,然后其他粒子跟踪当前的最优粒子在解空间中进行搜索[7]。
(2)评估单元的开发背景分析。对开发历程的了解与把握,采油厂具有相当大的优势。一个评估单元往往具有较长的开发历程,对这个历程各阶段及其变化的了解程度有助于SEC储量评估的准确性。如某评估单元就是一个典型例子(见图3),单元整个开发历程划分为五个阶段,每个阶段及其转换期的评估参数选取存在较大差异。
初始化的PSO 是一组随机解,通过迭代计算出种群中的最优解。粒子在每一次迭代过程中更新自己的速度和位置依据两个极值。一个是粒子自身找到的最优解为个体极值Pbest,另一个是目前在整个种群中找到的最优解为全局极值Gbest[8]。在第k+1 次迭代计算时,粒子i 根据下列规则来更新自己的速度和位置[9]。

其中,i =1,2,…n 为粒子的编号,xi表示粒子的位置,vi表示粒子的速度,ω 为惯性因子,c1、c2为加速常数,通常c1=c2=2,r1、r2为[0,1]之间的随机数,Pbest是粒子迄今为止搜索到的最优适应值,Gbest是整个粒子群迄今为止搜索到的最优适应值。局部搜索和全局搜索在解决各类问题时都起着相当重要的作用,而惯性因子ω 决定搜索性能。
2.2 改进的粒子群算法
由2.1 节知惯性因子ω 对局部搜索和全局搜索能力影响非常大,在算法初期时较大的惯性因子ω有利于扩大搜索空间和探索更多的未知区域,在算法后期收敛时较小的惯性因子ω 有利于对得到的最优区域进行微调,从而提高算法搜索的准确度,因此本文采用自适应动态赋值的惯性因子使得比固定值得到更好的寻优结果。
如果只对式(2)中惯性因子ω 单一的线性减少,这会使得搜索的步长逐渐减小,从而迭代过程渐渐地收敛到极值,这样的好处是易于收敛,但没有充分利用目标函数的其他信息,导致搜索空间狭小、过早收敛且易于陷入局部极值。为了解决上诉问题,本文引入目标函数提供的相关信息调整惯性因子ω 的值,构造衰减的指数函数exp(-k),保证ω 的取值范围在[0,1],惯性因子取值公式如下:
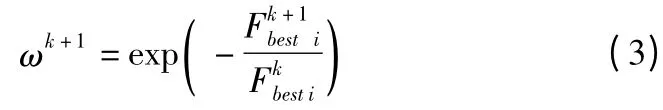
2.3 改进的粒子群算法对PID 参数优化
利用PSO 算法来优化PID 控制器中的Kp、Ki、Kd3个参数,将这3 个参数看作是粒子群中的3 个粒子,在搜索空间中找到最优的位置就是最优的PID 参数[10]。
PSO 优化算法步骤如下:
(1)初始化粒子群,并随机产生所有粒子的位置和速度;
(2)以当前的粒子位置作为PID 参数,按照公式(1)计算控制量u(t),得出转速误差e(t);
(3)循环步骤(2)得到绝对误差积分,作为PSO适应度评价标准;局最优适应值Gbest及其对应的最优值Fbest;
(4)对每个粒子,计算个体最优适应值Pbest和全
(5)根据式(2)更新粒子的速度和位置;
(6)如果没有满足终止条件(通常为预设的迭代次数和适应值下限值),则返回步骤(2),否则,退出算法,得到最优解作为PID 的参数。

图2 PSO-PID 自适应控制算法流程图
本系统初始化粒子群规模n=30,粒子向量v=30组随机数,搜索空间维数D =3,每0.1μs 采样一次速度返回值,每粒例子根据返回值与评价函数来更新自己的个体极值和自己当前的速度值,直到满足最大迭代次数30 或最小适应值为1。比例系数取值范围为[0,300];积分系数取值范围为[0,1];微分系数取值范围为[0,2]。改进的粒子群算法在优化PID 控制器系数的仿真实验中找出一组最优系数为:Kp=206.1549;Ki=0.9398;Kd=1.3012。并计算得出如图3 所示粒子群中的最优个体适应值为Fbest=2.2476。

图3 最优个体适应值图
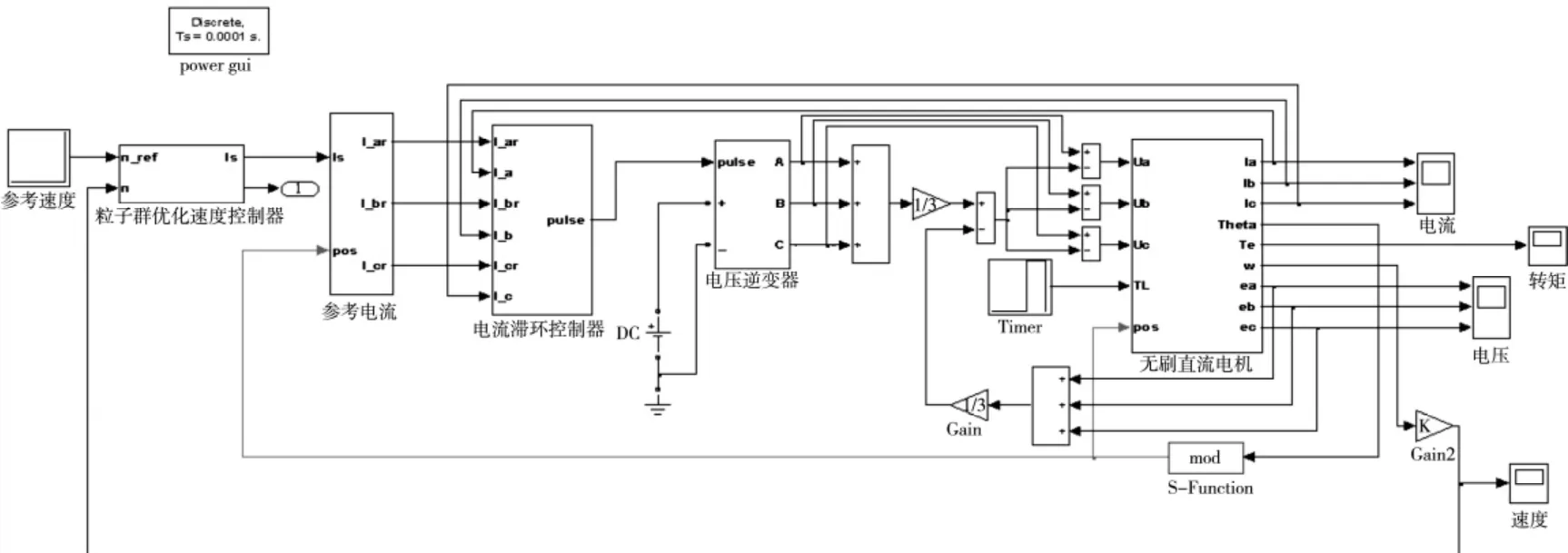
图4 Matlab/Simulink 中BLDC 仿真建模整体控制框图
3 仿真
依据无刷直流电机的控制模型在Matlab/Simulink 环境下建立BLDC 双闭环控制系统仿真模型如图4 所示。
在仿真系统中,无刷直流电机参数设置为:定子相绕组电阻r=1Ω;定子相绕组自感L=0.02H,互感M=-0.06H;转动惯量J=0.005kg·m2;极对数p=1;阻尼系数B=0.0002N·m·s/rad;220V 直流电源供电。在第一种加速情况下:系统空载启动时额定转速nref=900r/min,在t =0.2s 时加负载TL=1Nm,在t=0.5s 加速到nref=1100r/min,运行仿真模型得到基本粒子群算法优化加速时的转速和转矩响应曲线如图5 所示和改进的粒子群算法优化加速时的转速和转矩响应曲线如图6 所示。

图5 PSO 优化加速时转速和转矩响应曲线

图6 改进PSO 加速时转速和转矩响应曲线
在第二种加负载情况下:系统空载启动额定转速nref=900r/min,在t=0.3s 时加负载TL=1Nm,在t=0.5s 时再加负载TL=1.5Nm,在t=0.7s 时撤去负载,运行仿真模型得到基本粒子群算法加负载时的转速和转矩响应曲线如图7 所示和改进的粒子群算法加负载时的转速和转矩响应曲线如图8 所示。

图7 PSO 优化加负载转速和转矩响应曲线

图8 改进PSO 加负载转速和转矩响应曲线
由仿真波形图可以看出,在基于改进的PSO 算法优化PID 控制器控制下,第一种加速的情况下,改进前在电机启动时转速超调量较大,改进后时转速响应快速且平稳,超调小于1%,在t=0.2s 时突然加负载转速下降波动也小于改进前,在突然加速的条件下能保持响应快且超调小,并且迅速恢复到额定转速状态。第二种加负载的情况下,在t =0.3s 和t=0.5s 时分别突然加不同大小的负载,改进后转速下降较改进前波动小,在t =0.7s 时又撤去负载,改进后的转速上升波动小于2%,随即又快速恢复到稳定状态。转矩仿真波形图表明电机启动阶段转矩快速上升且恒定,当达到空载额定转速时,忽略摩擦转矩,电磁转矩均值为零。在突然施加和撤去负载时响应快速且波动小。根据仿真结果验证了采用基于改进的PSO 算法优化PID 控制器的无刷直流电机调速系统具有较好的动态特性和抗干扰性。
4 结论
本文针对传统PID 控制器对无刷直流电机复杂的多变量、耦合的、非线性的系统参数难以整定的情况,采用改进的PSO 算法对速度环PID 参数进行局部和全局的寻优在线优化,并建立了BLDC 双闭环控制系统。仿真验证了本控制系统转速响应迅速、超调量小,具有良好的跟随性和抗扰动性,从而说明改进的粒子群算法是一种有效的PID 优化方法,该改进粒子群算法的无刷直流电机控制方法可广泛应用其他PID 控制的系统中。
[1]殷云华,郑斌,郑浩鑫. 一种基于Matlab 的无刷直流电机控制系统建模仿真方法[J]. 系统仿真学报,2008,20(2):293-298.
[2]Z Gaing. A particle swarm optimization approach for optimum design of PID controller in AVR system [J]. IEEE Trans Energy Conversion,2004,19(2):384-391.
[3]Toscano R.A simple robust PI/PID controller design via numerical optimization approach[J]. Journal of Process Control,2005,15(1):81-88.
[4]赵亮,刘星桥,等. 基于DSP 的无刷直流电机模糊控制系统研究[J]. 电力电子技术,2009,43(5):40-42.
[5]何佳佳,侯再恩. PID 参数优化算法[J]. 化工自动化及仪表,2010,37(11):1-4.
[6]喻骁,刘东,兰维瑶. 基于PSO 算法的机械臂PID 控制器参数优化[J]. 组合机床与自动化加工技术,2011(2):89-92.
[7]李剑波,王东风,付萍,等. 基于改进粒子群算法的主汽温系统PID 参数优化[J]. 华北电力大学学报,2005,32(4):26-30.
[8]郝万君,强文义,等. 基于改进粒子群算法的PID 参数优化与仿真[J]. 控制工程,2006,13(5):29-32.
[9] Ji Zhen,Wang Yiwei,Chu Ying,et al. Bacterial particle swarm optimization[J]. Chinese Journal of Electronics,2009,18(2):195-199.
[10]刘东,冯全源,蒋启龙. 基于改进PSO 算法的磁悬浮列车PID 控制器参数优化[J]. 西南交通大学学报,2010,45(3):405-407.

