基于最小区域法的圆柱度几何误差评定*

黄 祥

(安徽国防科技职业学院 机械工程系，安徽 六安 237011)

0 引言

在机械工业生产中，不但要保证零件的尺寸精度，对形状精度和位置精度也有很高的要求。零件几何误差既可以作为验收零件的依据，又能够作为查找产生误差的本源，进而控制零件加工精度和装配精度，保证机械产品的质量。因此对零件几何误差评定理论与方法等众多问题的探讨与研究，在一段时间内成为计量领域中的热点之一。

零件几何误差的优化评定是一件比较复杂的工作，评定方法主要有最小二乘法、最小外接法、最大内切法及最小区域法，在现行中，对零件几何误差的评定多数情况下采用的是“最小二乘法”，此评定方法整个求解过程相对较为简便，但评定结果的精确度小，不能满足几何误差最小条件评定原则［1］。严格地按照最小条件进行评定的方法是最小区域法［2］，在数学范畴内属于极大值极小化问题、或者是极小值的极大化问题［3-4］。在构建典型几何误差评定规划模型的条件下，探究将最小区域法应用于圆柱度误差的优化评定中，实验表明该方法能够获得更高的精度和更快的速度，具有较好的评定效果和应用前景。

1 圆柱度误差评定模型的构建

几何误差是指零件的被测要素相对于理想要素之间的变动范围，决定零件几何误差大小的重要因素是理想要素所处的位置。在进行几何误差评定时，理想要素的位置必须符合最小条件原则，即为实际要素与理想要素之间的最大变动量应该最小。由此可知，要满足最小条件，与理想要素所在的位置关系密切，依据理想要素的位置和几何误差之间的关系，通过误差变换，建立圆柱度误差评定模型。

用两个同轴的理想圆柱去包容被测要素，当包容区域为最小时，包容区域的宽度就是圆柱度误差值，其圆柱度最小区域评定规划模型为:

在上式中:F 为目标函数，u 和v 为特征参量，分别表示理想外接柱最大半径和理想内接柱最小半径，被测点以(θi，zi，Ri)来表示，其中θi是转角参数，zi是轴向坐标，Ri是在采样点处所测得的半径值。

零件圆柱度误差评定模型是生产中最常见的具有典型特征的几何误差评定模型。

2 规划模型最小区域法的求解

对零件圆柱度误差评定规划模型的求解问题，可以归结为对复杂线性规划的求解。标准线性规划的可行域是一个凸多面体，如非空，一定有基本可行解;如有最优解，一定有最优基本可行解，因此在求解时，进行基本可行解的迭代即可。用基本可行解来说明最小区域法的寻优过程如下:①把标准线性规划的“约束方程组”用“典范型方程组”来表示，找出方程组的基本可行解，并且作为初始基本可行解;②若不存在基本可行解，则说明约束条件存在问题，方程组无解;③如果有基本可行解，将初始基本可行解作为始点，从可行性条件和最优条件入手，用非基变量替换某一基变量，这样在目标函数值中，就能求解得到更优的基本可行解;④按步骤③进行循环叠代，直至可行解满足最优条件，即得到问题的最优答案。

典范型线性规划模型可以表示为［5］:

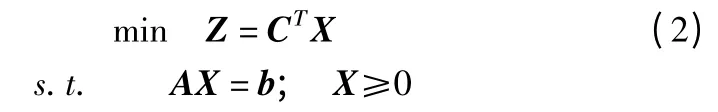
可写为:

式中，XB= (x1，x2，…，xm)Τ是基变量，XN= (xm+1，xm+2，…，xn)Τ是非基变量;A = (B，N)，其中B =(a1，a2，…，am)。

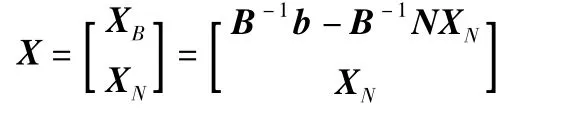
与其相应的目标函数值是:

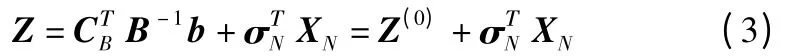
其中:

σN为与非基本变量XN对应的检验向量，若σN≥0，那么这个基本可行解就是最优解。在利用上述最小区域法求解线性规划问题时，在每次叠代计算的数据中，真正起作用的是以下的一些数据:①基本可行解XB=B－1b 及其相应的目标函数值Z =CΤBB－1b;②非基变量检验数σΤN=CΤN－CΤBB－1N 及其换入变量xk。③主元列元素B－1ak、换出变量xe，通过此两个量，可求出一组新的基变量和新的可行基B1，这里只须解出B1即可，上述数据均能从线性规划问题的原始数据中求解得出。任一基本可行解的关键数据，均能直接从原线性规划的典范型运用矩阵和向量中求解，这是最小区域法的特征之一，最小区域法的另外一个特征是对B－1的求解过程，即:当可行基从B 变换到B1时，B1－1的值通过B－1直接求出，显著减少求解过程中的工作量。

规划模型的最小区域法具体求解过程如下:

(1)先将一般线性规划问题转化为典范型;求解得到初始可行基B 的逆阵B－1，由此便可求出初始基本可行解XB=B－1b，XN=0;

(2)然后确定初始基本变量和初始可行基B，再

(3)算出乘子π=CBB－1，即能计算出目标函数的当前值为:Z=CBB－1b=πb;

(5)根据min{σj| σj＜0}=σk确定非基变量xk为换入变量，解出B－1ak，如果B－1ak≤0，说明线性规划问题的可行解集为无界，说明不存在有限最优解，至此求解过程结束，反之进入下一个步骤;

(7)用ak代替ae得到新基B1，由B1－1=EekB－1计算新基的逆阵B1－1，求出新的基本可行解XB=B1－1b，XN=0，重复步骤(3)～(7)，直至求出最优解。

3 应用示例

如图1 所示一阶梯轴(圆柱类零件)，基本尺寸为φ80mm，其尺寸特征规范为φ80e7○E，根据工作条件，圆柱度公差要求为t =0.015mm。采用6 截面等间距周线测量法进行数据的提取，利用本文方法评定该轴段圆柱度误差，并判断圆柱度是否符合要求。

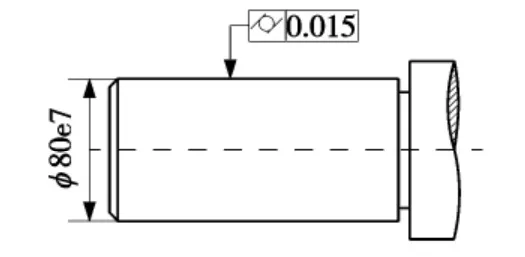
图1 被测轴

图2 圆柱度评定结果可视化

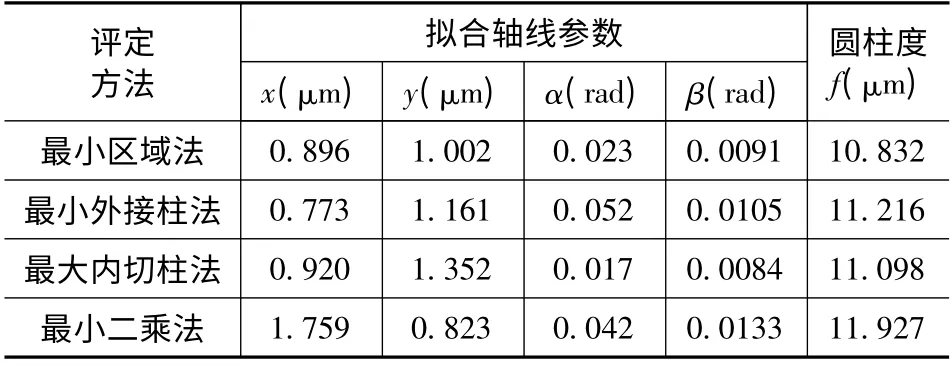
表1 圆柱度评定结果 单位(μm)

表2 与其它方法的最小区域法评定结果比较

图2 为被测轴段圆柱度最小区域包容评定的三维效果图，表1 为圆柱度四种评定方法的评定结果，规划模型求解方法采用本文提出的最小区域法。由结果可以知道，最小区域法圆柱度f =10.832μm ＜t=0.015mm，则可以判断该轴段圆柱度是合格的。遗传算法［6］和最速下降算法［7］也是工程中常用的优化算法，都可用于求解评定模型，表2 列出了三种优化算法对测量数据最小区域法评定结果的对比，从表中数据分析得出，最小区域算法评定值与遗传算法的评定值很接近，但是明显小于最速下降法评定的值，由此可知，用最小区域法能够求出圆柱度误差更为精确的值，同时可以看出，在前述中所建立的圆柱度误差评定规划模型是正确的。

4 结论

构建正确的误差评定数学模型，并采用合适的优化算法，是保证几何误差精确评定的关键。在分析的基础上，建立了基于几何误差特征的圆柱度误差评定数学模型，将规划模型转化为线性规划问题，提出将最小区域法应用于圆柱度误差模型的优化求解中，提高了规划模型的求解精度和求解速度。实验表明，采用最小区域法评定圆柱度误差的正确性和可行性，这为机械工程中圆柱度误差的快速而准确的评定提供了理论基础和技术支持，并可推广到零件其它几何误差评定。

［1］ISO/TS 17450－1:2000(E)Geometrical Product Specification (GPS)—General concepts—Part 2:Model for geometrical specification and verification［S］.

［2］李秀明，石照耀. 基于凸多边形的直线度误差的评定［J］. 机械科学与技术，2008，27(6):736－738.

［3］沈先钊. 圆度、圆柱度和同轴度计算机测量数据最小区域法处理算法研究［J］. 中国机械工程，2003，14(17):1472－1473.

［4］郑鹏，张琳娜. 形状误差目标函数单谷性的分析与研究［J］. 计量与测试技术，2007，34(11):16－18.

［5］粟时平，李圣怡，王贵林. 基于鞍点规划法的形位误差计算机评定［J］. 计量学报，2003，24(1):26－28.

［6］施展. 基于遗传算法的回转体零件轮廓度误差评定方法［J］. 工具技术，2002，36(8):58－60.

［7］N. Parthasarathy. Minimum zone cylindricity evaluation using Steepest descent method［D］.University of Cincinnati，Master degree，2004.