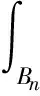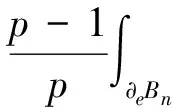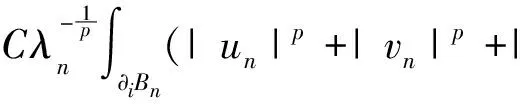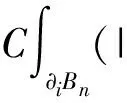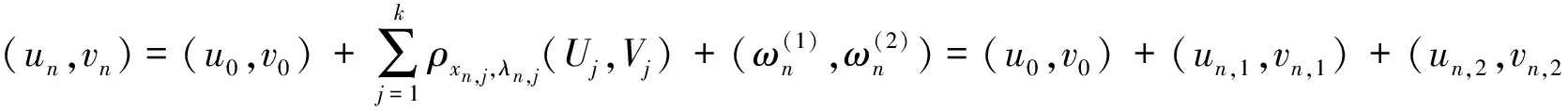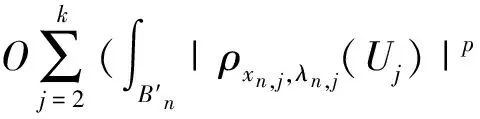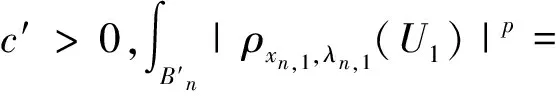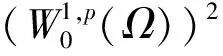带有齐次函数和临界指数的椭圆方程组的研究

康东升，张微微，吴 红

(中南民族大学 数学与统计学学院，武汉430074)

1 问题引入

本文研究下列椭圆方程组

(1)

假设参数满足下面条件：

c1(|u|p+|v|p)≤Q(u,v)≤c2(|u|p+|v|p).

(H3)Qu(u,v),Qv(u,v)对任意u,v严格递增,则存在:

Qu(u,v)≤M1(|u|p-1+|v|p-1),

Qv(u,v)≤M2(|u|p-1+|v|p-1).

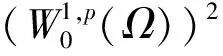
u0,v0≠0,(u0,v0),(φ,ψ)=0,∀(φ,ψ)∈((Ω))2.

近年来带有Hardy项和临界Sobolev指数的方程受到关注[1,2],但主要是对半线性方程的研究如文献[3],近几年才扩展到拟线性问题上来如文献[4],2012年文献[5]通过局部紧性理论研究了拟方程无穷解的存在性,本文基于此来研究此方程组的无穷解.

本文中因为临界指数p*的存在,I0(u,v)在大范围中不满足P-S条件,所以建立如下扰动方程组及相应能量泛函：

(2)

本文的结果可归结为下面的两个定理.

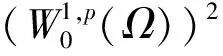
定理2 假设(H1),(H2),(H3)成立,则方程组(1)有无穷解.

2 预先结果

引理1 当ε=εn→0时,(un,vn)是方程组(2)的解,满足‖(un,vn)‖≤C.

(ii)对i,j=1,…,k,若i≠j,则当n→∞时

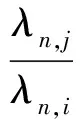
证明过程与文献[5]中附录D相似,故省略.

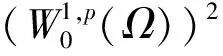
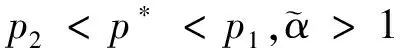
(3)

的解,A>0是充分大的常数.

由比较原则|un(x)| ≤wn(x),|vn(x)| ≤wn(x).

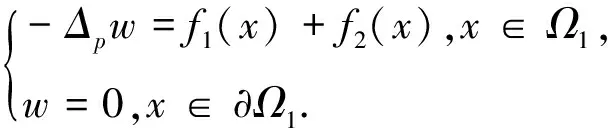
引理3[5]w是方程

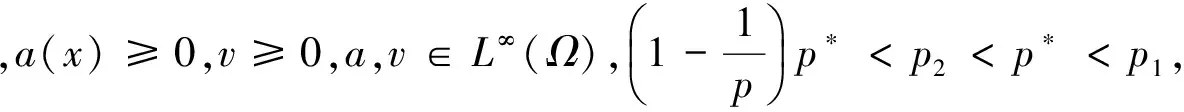
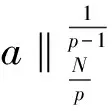
引理4w是方程

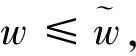
通过引理2可得：

‖C+Cw1‖q1≤C′+C‖w1‖q1≤

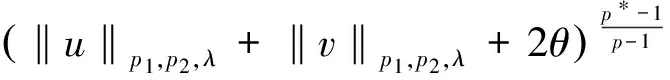
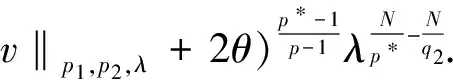
引理5 (u,v)是方程组

的解且(u,v)∈(W1,p(RN))2,α+β=p*,则：

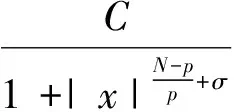
证明证明过程与文献[5]附录B解的衰退估计相似,故省略.

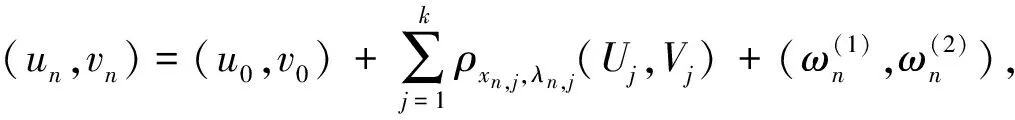
证明由引理4和引理6可直接得证.

3 在安全区域的估计

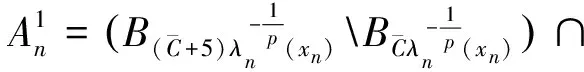
不包括(un,vn)的任意集中点,这个区域我们称作(un,vn)的安全区域.

证明证明与文献[5]相同,故省略.

(4)

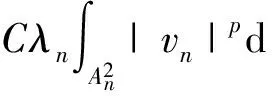
(5)

因此

(6)

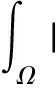
则(4)式得证,同理(5)式得证,由(4)和(5)式及引理8可得：

4 主要结果证明

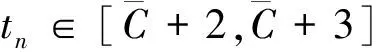
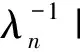
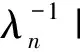
(7)

利用引理8 及(6)和(7)式可得：

(8)

定理1证明我们有以下两种情形：

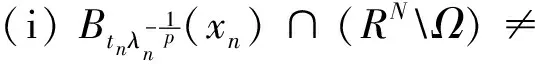
F(un,vn,x,x0,v)=

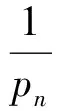
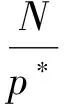
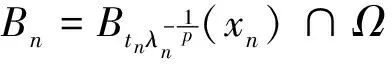
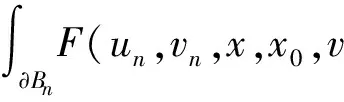
(9)

情形(ii)取x0=xn.

因为pn

(10)

把∂Bn分解为∂Bn=∂iBn∪∂eBn,其中∂iBn=∂Bn∩Ω,∂eBn=∂Bn∩∂Ω.

在∂Ω上un=vn=0中,则：

(11)

且当n→∞时,‖un,2‖+‖vn,2‖→0，通过引理5,若N>p2,则：

(13)

因为在RNΩ中,un=0,vn=0.

(14)

(15)

假设(ρxn,1,λn,1(U1),ρxn,1,λn,1(V1))是所有爆破项中有最小集中率的,则：

同理

(16)

因此存在常数c′>0满足：

(17)

同理

(18)

由(14)～(18)式得：

(19)

[1]Hardy G,Littlewood J,Polya G. Inequalities[M]. Cambridge: Cambridge University Press,1988: 239-243.

[2]Egnell H. Elliptic boundary value problems with singular coefficients and critical nonlinearities [J]. Indiana Univ Math,1989,38(2): 235-251.

[3]Bahri A,Coron J M. On a nonlinear elliptic equation involving the critical Sobolev exponent [J]. Comm Pure Appl Math,1988,41:253-294.

[4]Azorero J,Peral I. Existence and nonuniqueness for thep-Laplacian [J]. Comm Partial Differential Equations,1987,12: 1389-1430.

[5]Cao D,Peng S,Yan S. Infinitely many solutions forp-Laplacian equation involving critical Sobolev growth [J]. J Funct Anal,2012,262:2861-2902.

[6]Rabinowitz P. Minimax methods in critical points theory with applications to differential equations [M]. Washington: American Mathematical Society,1986: 7-50.

[7]Ambrosetti A,Rabinowitz P. Dual variational methods in critical point theory and applications [J]. J Funct Anal,1973,14:349-381.

[8]Cao D,Yan S. Infinitely many solutions for an elliptic problem involving critical Sobolev growth and Hardy potential [J].Calc Var PDE,2010,38:471-501.