基于算子α的活性序及其性质研究

段 汕，徐 文，罗 敬，贺 兴

(中南民族大学 数学与统计学学院，武汉 430074)

作为图像处理中一个强有力的工具，数学形态学是一门建立在严格数学基础上的学科，其基本思想和方法对图像处理的理论和技术产生了重要影响[1].数学形态学具有的完备数学理论，为形态学方法用于图像分析和处理等各项工程技术领域奠定了坚实的基础，同时这也使得数学形态学中数学理论的研究显得尤其重要[2，3].

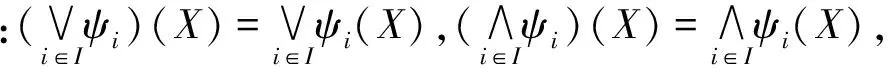
本文在此基础上以O(L,M)上序关系的研究为主题，探讨了其上一类新的偏序关系[8]，它不同于继承序，与文献[3]、[4]中所研究的活性序(activity ordering)相关但更具一般性，我们称之为基于α的活性序，这里α为O(L,M)上的任一算子.对于这一新的二元关系我们不仅证明了它是O(L,M)上的一偏序关系，同时证明了O(L,M)在此序关系下仍然构成完备格.此外，对其相关的结构及性质进行了深入的研究，为O(L,M)中序关系的建立提供一个统一的框架.对于与此相关的中心算子的建立，为基于α的活性序下算子各种性质的讨论及应用奠定了理论基础.

1 预备知识

一个格的每个子集都有上下确界，这个格称为完备格.给出两个完备格L和M，L到M上所有算子的集合用O(L,M)表示,O(L,M)继承了完备格M上的偏序结构，在这种偏序结构下O(L,M)构成了一个完备格.O(L,M)上的最小元是把L上每个元素都映射到M的最小元的算子，记作o,O(L,M)上最大元是把L上每个元素都映射到M的最大元的算子，记作ι.

一个有唯一余元的可分配格称为布尔格，布尔格上每一个元素X的余元记作X*.我们把将元素X映射到其余元X*的算子记作v,即v(X)=X*.若完备格L和M也是布尔格，对于每个算子ψ∈O(L,M)定义其负算子ψ*∈O(L,M)为ψ*=vψv,不混淆时也记作ψ*(X)=[ψ(X*)]*，对于算子ψ∈O(L,M)定义其余算子ψc为ψc(X)=[ψ(X)]*.

2 基于给定算子α的活性序及其性质

2.1 基于α的活性序

在完备格(O(L,M)，≤,∨,∧)上，文献[3]、[4]中针对单位算子给出了活性序的概念，我们用O(L,M)上的任一固定算子α代替单位算子，提出O(L,M)上基于算子α的一种偏序关系.

定义1 设L是完备格，M是完备布尔格，α是O(L,M)上任意给定的算子，如果完备格(O(L,M)，≤,∨,∧)中任意的两个算子φ、ψ满足条件：

α∧ψ≤α∧φ,α∨ψ≥α∨φ.

(1)

则称算子ψ比算子φ相对于α更具活性，记作φ⪯ψ.

M是完备布尔格具有可分配性，所以下列等式成立：

αc∨(α∧ψ)=(αc∨α)∧(αc∨ψ)=αc∨ψ,

αc∧(α∨ψ)=(αc∧α)∨(αc∧ψ)=αc∧ψ.

其中αc：αc(X)=[α(X)]*是算子α的余算子.于是由条件(1)可推得：

αc∨ψ=αc∨(α∧ψ)≤αc∨(α∧φ)=αc∨φ,

αc∧ψ=αc∧(α∨ψ)≥αc∧(α∨φ)=αc∧φ.

由此可得定义1的等价定义：

定义2 设L是完备格，M是完备布尔格，α是O(L,M)上任意给定的算子，如果完备格(O(L,M),≤,∨,∧)中任意的两个算子φ、ψ满足条件：

αc∨ψ≤αc∨φ,αc∧ψ≥αc∧φ.

(2)

则称ψ比φ相对于α更具活性，记作φ⪯ψ.

下面我们对完备格(O(L,M),≤,∨,∧)上给出的“⪯”这种新的二元关系进行研究.

性质1 如果L是一个完备格，M是一个完备布尔格，则“⪯”是(O(L,M),≤,∨,∧)上的一个偏序关系.

证明①自反性.由于α∧ψ≤α∧ψ和α∨ψ≥α∨ψ显然成立，故由(1)式可知ψ⪯ψ成立.

② 传递性.若φ⪯ψ，ψ⪯β.由(1)式可知α∧ψ≤α∧φ、α∧β≤α∧ψ,则α∧β≤α∧φ；α∨ψ≥α∨φ、α∨β≥α∨ψ，则α∨β≥α∨φ，从而φ⪯β成立.

③ 反对称性.若φ⪯ψ，ψ⪯φ.由(1)式可知α∧ψ≤α∧φ、α∧ψ≥α∧φ，则α∧ψ=α∧φ;αc∧ψ≥αc∧φ、αc∧ψ≤αc∧φ，则αc∧ψ=αc∧φ成立，故ψ=ψ∧(αc∨α)=(ψ∧αc)∨(ψ∧α)=(φ∧αc)∨(φ∧α)=φ∧(αc∨α)=φ,由①、②、③即知“⪯”是(O(L,M),≤,∨,∧)上的一个偏序关系.

由性质1可以看出“⪯”这种二元关系是一种与继承序相关但又不同于继承序的偏序关系，它是在(O(L,M),⪯,∨,∧)的基础上建立的，我们把它称为基于α的活性序.下面我们研究这种序关系的一些基本性质.

2.2 基于α的活性序的性质

性质2 设L是一个完备格，M是一个任意的完备布尔格，对于O(L,M)上任意的两个算子φ、ψ，有下列关系成立：

(a)若ψ≤φ≤α，则φ⪯ψ； (b)若α≤φ≤ψ，则φ⪯ψ.

证明(a)由于ψ≤φ≤α，有α∧ψ=ψ≤φ=α∧φ、α∨ψ≥α=α∨φ成立，故由(1)式可知φ⪯ψ成立.

(b)由于α≤φ≤ψ，有α∧ψ≤α=α∧φ、α∨ψ=ψ≥φ=α∨φ成立，故由(1)式可知φ⪯ψ成立.

由性质2可以看出基于α的活性序“⪯”与继承序“≤”之间的联系：O(L,M)上的算子越远离固定算子α，越具有活性.除此之外，基于α的活性序“⪯”本身还具备以下性质3.

性质3 设L、M是两个任意的完备布尔格，对于O(L,M)上任意的3个算子φ、ψ、θ，有下列关系成立：

(a)α⪯ψ⪯αc；(b)φ⪯ψ则θ∧φ⪯θ∧ψ和θ∨φ⪯θ∨ψ成立；

(c)φ⪯ψ⟺ψc⪯φc；(d)当α=α*时，φ⪯ψ⟺φ*⪯ψ*.

证明(a)由于α∧ψ≤α=α∧α、α∨ψ≥α=α∨α，故由(1)式可知α⪯ψ；同理由α∧αc≤α∧ψ、α∨αc≥α∨ψ可知ψ⪯αc，故α⪯ψ⪯αc成立.

(b)由于φ⪯ψ，可知α∧ψ≤α∧φ、α∨ψ≥α∨φ成立，故有

α∧(ψ∧θ)=(α∧ψ)∧θ≤(α∧φ)∧θ=

α∧(φ∧θ)，

α∨(ψ∧θ)=(α∨ψ)∧(α∨θ)≥(α∨φ)∧(α∨θ)=α∨(φ∧θ).

故由(1)式可知θ∧φ⪯θ∧ψ成立.同理，

α∧(ψ∨θ)=(α∧ψ)∨(α∧θ)≤(α∧φ)∨(α∧θ)=α∧(φ∨θ)，

α∨(ψ∨θ)=(α∨ψ)∨θ≥(α∨φ)∨θ=

α∨(φ∨θ).

由(1)式可知θ∨φ⪯θ∨ψ成立.

(c)若φ⪯ψ，可知α∧ψ≤α∧φ、α∨ψ≥α∨φ成立，根据德摩根律，对两式左右两边同时取余运算可得αc∨ψc≥αc∨φc、αc∧ψc≤αc∧φc，再由(2)式可知ψc⪯φc成立.同理若ψc⪯φc，根据(2)式可知αc∨ψc≥αc∨φc、αc∧ψc≤αc∧φc成立，对两式左右同时取余运算可得α∧ψ≤α∧φ、α∨ψ≥α∨φ，再由(1)式可知φ⪯ψ成立.综上所述φ⪯ψ⟺ψc⪯φc成立.

(d)若φ⪯ψ，可知α∧ψ≤α∧φ、α∨ψ≥α∨φ成立，根据德摩根律，对两式左右两边同时取负运算可得α∨ψ≥α∨φ、α∧ψ≤α∧φ，由α=α可得α∨ψ≥α∨φ、α∧ψ≤α∧φ，再由(2)式可知φ⪯ψ成立.同理，若φ⪯ψ根据(1)式可知α∨ψ≥α∨φ、α∧ψ≤α∧φ成立，又由α=α即可得α∨ψ≥α∨φ、α∧ψ≤α∧φ，根据德摩根律，对两式左右两边同时取负运算可得α∧ψ≤α∧φ、α∨ψ≥α∨φ，故由(1)式可知φ⪯ψ成立.综上所述当α=α时，φ⪯ψ⟺φ*⪯ψ.

由上述性质可以看出，O(L,M)中各种算子包括了它们的余算子和自对偶条件下的负算子在新的序结构“⪯”下具有的关系,在下面的性质4中，我们将为O(L,M)在“⪯”上结构的研究提供一个基础.

性质4 设L是一个完备格，M是一个完备布尔格，O(L,M)上的算子φ、ψ满足条件φ≤ψ.令：

γ=(α∧ψ)∨φ=(α∨φ)∧ψ,

(3)

κ=(αc∧ψ)∨φ=(αc∨φ)∧ψ.

(4)

则下列关系成立：

(a)α∧γ=α∧ψ,α∨γ=α∨φ,α∧κ=α∧φ,α∨κ=α∨ψ，αc∧γ=αc∧φ,αc∨γ=αc∨ψ，αc∧κ=αc∧ψ，αc∨κ=αc∨φ.

(b)γ⪯φ,ψ；如果γ′是其它任意满足γ′⪯φ,ψ的算子，则γ′⪯γ.

(c)φ,ψ⪯κ；如果κ′是其它任意满足φ,ψ⪯κ′的算子，则κ⪯κ′.

(d)对于每一个O(L,M)中的算子η，φ≤η≤ψ⟺γ⪯η⪯κ.

证明(a)由φ≤ψ可知α∧φ≤α∧ψ，αc∧φ≤αc∧ψ,

又由(3)、(4)两式可得α∧γ=α∧[(α∧ψ)∨φ]=(α∧ψ)∨(α∧φ)=α∧ψ,

α∨γ=α∨[(α∧ψ)∨φ]=α∨φ,

α∧κ=α∧[(αc∧ψ)∨φ]=(α∧αc∧ψ)∨(α∧φ)=α∧φ,

α∨κ=α∨[(αc∨φ)∧ψ]=(α∨αc∨φ)∧(α∨ψ)=α∨ψ,

αc∧γ=αc∧[(α∧ψ)∨φ]=αc∧φ、αc∨γ=αc∨[(α∨φ)∧ψ]=αc∨ψ,

αc∧κ=αc∧[(αc∧ψ)∨φ]=(αc∧ψ)∨(αc∧φ)=αc∧ψ,

αc∨κ=αc∨[(αc∧ψ)∨φ]=αc∨φ,

(b)由φ≤ψ和(a)的结论可知α∧γ=α∧ψ≥α∧φ，α∨γ=α∨φ≤α∨ψ,

故由(1)式可得γ⪯φ,ψ.若γ′⪯φ,ψ，则由(1)式可知α∧γ′≥α∧ψ=α∧γ,α∨γ′≤α∨φ=α∨γ，故γ′⪯γ成立.

(c)由(4)式和φ≤ψ可得αc∨κ=αc∨[(αc∧ψ)∨φ]=αc∨φ≤αc∨ψ，αc∧κ=αc∧[(αc∨φ)∧ψ]=αc∧ψ≥αc∧φ,故由(3)、(4)两式可知φ,ψ⪯κ成立.若φ,ψ⪯κ′，同理可知αc∨κ′≤αc∨φ=αc∨κ、αc∧κ′≥αc∧ψ=αc∧κ，再由(3)、(4)两式可知κ⪯κ′成立.

(d)若φ≤η≤ψ成立，由(a)的结论可知α∧κ=α∧φ≤α∧η≤α∧ψ=α∧γ，α∨κ=α∨ψ≥α∨η≥α∨φ=α∨γ，故由(1)式可知γ⪯η⪯κ成立.若γ⪯η⪯κ成立，则由(1)、(2)两式可知α∧κ≤α∧η≤α∧γ，αc∧κ≥αc∧η≥αc∧γ，再由(a)的结论可得:

φ=(αc∨α)∧φ=(αc∧φ)∨(α∧φ)=(αc∧γ)∨(α∧κ)≤(αc∧η)∨(α∧η)=η,

ψ=(αc∨α)∧ψ=(αc∧ψ)∨(α∧ψ)=(αc∧κ)∨(α∧γ)≥(αc∧η)∨(α∧η)=η,即φ≤η≤ψ成立.综上所述φ≤η≤ψ⟺γ⪯η⪯κ.

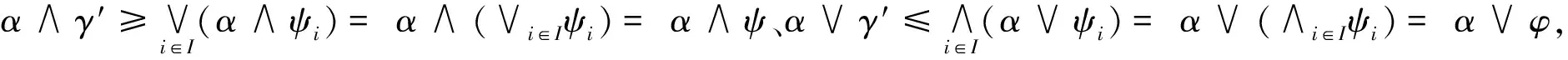
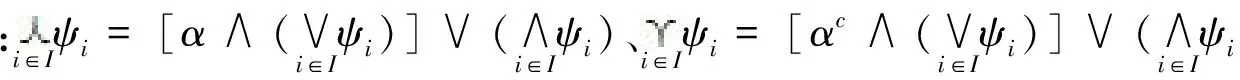
性质6 设L是一个完备格，M是一个完备布尔格，ψ是O(L,M)上的任一算子，则有下列等式成立：oψ=α∧ψ，oψ=αc∧ψ，ιψ=α∨ψ，ιψ=αc∨ψ.

证明由性质5可知:

oψ=[α∧(o∨ψ)]∨(o∧ψ)=α∧ψ,

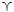
ιψ=[α∧(ι∨ψ)]∨(ι∧ψ)=α∨ψ,

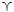
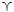
性质7 设L和M是两个完备布尔格，{ψi},i∈I是O(L,M)上任意的算子族，则下列等式成立:

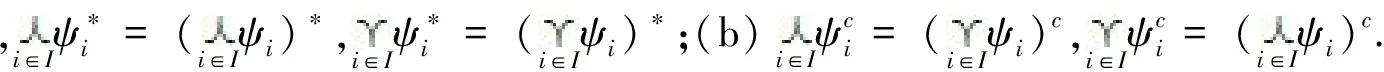
证明(a)由性质5和德摩根律可知:

(b)同理由德摩根律可知:

3 结束语

序关系的研究在数学形态学理论和实际应用中都有着重要的研究价值，通过以上研究，我们在继承序的基础上,探讨了一类新的序关系即基于α的活性序，它不仅是O(L,M)上的一偏序关系，并且O(L,M)在这种偏序关系下构成一个完备格.本文为O(L,M)中序关系的建立提供了一个统一的框架，也为基于α的活性序下算子各种性质的讨论及应用奠定了理论基础，对算子空间中序关系的理论研究和实际应用有一定指导意义.

[1]Shin F R. Image processing and mathematical morphology fundamentals and applications[M].New York: CRC Press,2009.

[2]Serra J.Image analysis and mathematical morphology[M].New York:Academic Press,1982.

[3]Serra J.Image analysis and mathematical morphology Ⅱ:theoretical advances [M]. New York: Academic Press,1988.

[4]Heijmans H.Morphological image operator[M]. Boston:Academic Press,1994.

[5]Kislitsyn S S.A finite partially ordered set and its corres-ponding set of permutations[J].Mathematical Notes of the Academy of Sciences of the USSR,2005,4(5):511-518.

[6]Martinez J E,Singer I.Dualities between complete lattices[J].Optimization,1990,21(4):481-508.

[7]Abraham U.On poset Boolean algebras[J].Order,2003,20(3):265-290.

[8]Heijmans H.Morphological filtering and iteration[J].Proc SPIE,1990,1360: 166-175.