泵站能效累计运行时间多目标优化调度

唐玉玲，郑贵林

(1武汉大学 动力与机械学院，武汉 430072；2中南民族大学 计算机科学学院，武汉 430074)

提升能源系统的效率是“节能”的基本手段，多年来获得了广泛的研究和关注.Xia Xiaohua等将能源系统的能效分成POET 4个层次：性能效率、运行效率、设备效率和技术效率[1].泵站作为典型的能源转换系统，其能效主要从性能效率和运行效率两个层次进行提升.文献[2]通过对泵的运行状态进行优化实现最优运行效率.在开展优化控制研究时，多种优化计算方法，例如，遗传算法[3]、基因算法[4]等都被用于水泵的优化控制.文献[5,6]研究了泵的能耗模型，这是能效优化的基础.对于大多数泵站，用水量即是峰谷电价(TOU)能效研究中的重要影响因素.文献[7,8]对用水量预测进行了探讨.文献[9]研究了基于分时电价的泵站优化调度方法，获得了泵的最优化启停序列.文献[10-12]研究了复杂电价下定速泵站能源效率的模型预测控制方法.文献[13]考虑了峰谷电价、潮汐变化等因素，研究了泵站多机组变速优化问题.

为了确保流程可靠性，泵站一般都配置备用泵组.最佳运行方式是将运行任务均分给各泵组，使各泵组的累计运行时间最终趋于一致.这样便于统一安排泵组的检修计划，节省人力成本.并能有效避免某些泵组运行时间长需要提前改造而某些泵组却长期停运的问题.目前，泵站的备用调度主要依靠人工完成，无法实现基于泵组累计运行时间的优化调度.另一方面，泵站优化调度研究也主要考虑能源效率因素，尚未较好地将泵的累计运行时间融入优化问题.

本文拟在泵站优化调度中同时考虑能源效率和累计运行时间两个因素，分别建立峰谷电价下泵站能源费用及泵组累计运行时间差两个目标函数，进行多目标优化.鉴于多目标优化问题的非线性特征，采用粒子群优化算法(PSO)进行优化求解.以一座水厂取水泵站为例进行仿真研究，验证此优化调度方法的有效性.

1 优化调度方法研究

1.1 能效优化

在并列配置M+1台泵组的泵站中，一般M台泵组参与任务调度，而将1台泵组置于备用状态.泵站在调度时间段[t0,tf]内的运行费用为：

(1)

式中，Pei(t)为i泵组的功率，kW；p(t)为电价函数，元/kW·h；ui(t)为i泵组的状态函数.

(2)

ui(t)为“1”表示i泵组在t时刻处于运行状态，反之则处于停止状态.

取水泵站以定速泵为主，故以下只针对定速泵进行研究.定速泵的能耗与泵的扬程、流量以及泵和电机的效率有关，可以写为：

(3)

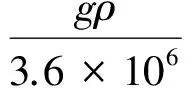
H=H0-sQ2,

(4)

H0为泵的最大扬程，s为与摩擦有关的系数.泵的管路特性曲线可表示为：

H=HT-WL+srQ2,

(5)

式中，HT为最大提升高度，m,泵安装完成后HT为常数,sr为与摩擦有关的系数，WL为取水口水位，m.定速泵的实际工作点[Qr,Hr]是曲线(4)和(5)的交点，工作点的效率表示为：

(6)

式中，a、b和c为常系数.结合式(1)和(3)并离散化得：

(7)

(8)

subject to

1.2 效率累计运行时间多目标优化

能效优化问题(8)仅考虑了泵站的运行费用单一目标，没有考虑泵组的累计运行时间.一台泵的累计运行时间可以表述为：

(9)

(10)

DT越小，则各泵组累计运行时间越接近.将DT也作为取水泵站的优化调度的目标函数，与能效一起构成多目标优化问题：

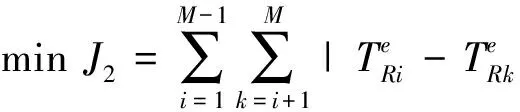
(11)

subject to

直接求解多目标优化问题一般比较复杂，在工程中可将多目标转换为单目标进行优化.本文通过平衡系数Φ将PE和DT合成一个目标函数，构成单目标优化问题：

(12)

subject to

通过Φ可以调整两个目标之间的权重，满足不同的调度需求.特别地，当Φ=0.0时，该多目标优化问题退化为能效单目标优化.

2 实例研究

2.1 实例分析

本文以某水厂取水泵站为实例进行研究.该泵站配置3台定速泵，性能曲线均为H=22.617-9.44×10-7Q2；对应的管道特性曲线为H=HT-WL+1.83×10-7Q2.根据设计规范HT为15 m.泵组取水口位于入海口，受潮汐影响水位WL跟随时间变化.泵效率曲线的系数为：a=-1.298×10-7，b=0.0006597，c=-0.04336.此水厂清水池底面积A=4000 m2，最高水位为4 m.在常规运行模式下，仅2台泵组运行，而另外1台泵组用作备用.此区域的峰谷电价为：

(13)

式中，ps为平段电价，ps=0.7元/kW·h；pp为高峰电价，pp=1.58ps；po为低谷电价，po=0.5ps.

峰谷电价、用水量以及取水口水位都具有以24 h为周期的特征，故将优化调度时段取为24h.将采样时间设置为Ts=15 min，故N=(t0-tf)/Ts=96.针对取水泵站优化调度问题，需要处理的约束主要包括：

1)清水池水位约束:

(14)

(15)

2)总取水量约束:

(16)

3)优化变量约束:

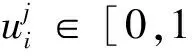
(17)

2.2 优化问题的求解

(1)能效优化问题.

在取水泵站能效单目标优化调度问题(8)中，优化变量为泵的开/关状态(“1”或“0”)，属于0-1整数规划问题.为了方便,本文采用Matlab优化工具箱中的bintprog函数进行优化求解.

(2)能效运行时间多目标优化问题.

将累计运行时间引入目标函数(12)后，由于引入了绝对值和项，故目标函数呈现非线性特征，采用常规0-1整数规划算法无法求解.粒子群优化算法具有多点搜索、计算简单等特点[16,17]，适合问题(12)的求解.

(18)

(19)

3 仿真结果

图1 用水量及取水水位

首先，对能效优化调度方法进行仿真分析，结果如图2所示.优化指令将泵组P1、P2的工作时段调度到非高峰时段，并在高峰时段停运泵，以获得最小的能源费用.从图2还可以看出清水池水位一直处于高限和低限之间，满足了系统的约束条件.

图2 能效优化调度方法仿真结果

(20)

图3 能效累计运行时间多目标优化调度方法

从图3还可以看出：当Φ=0.0，不考虑累计运行时间的影响，P1、P2运行时间被均匀调度；当Φ=1.0或3.0时，P2的运行时间明显长于P1，两者累计运行时间的差值明显缩小.例如，Φ=3.0时，在调度时段结束时P1、P2的累计运行时间分别203.25 h和167.25 h.经过一个调度时段，两者累计运行时间差从50 h减小到了36 h.可以推知：经过多个优化时段后，P1、P2的累计运行时间将趋于一致；另外，经历多次备用切换后，P1、P2、P3三台泵组累计运行时间差也将逐渐缩小.

能效单目标优化及能效累计运行时间多目标优化的性能统计如表1所示.2种方法都将泵组的运行时段调度到电价非高峰时段，有效降低了能源费用.随着多目标优化平衡系数Φ的增大，优化指令更多地注重累计运行时间差，在一定程度上牺牲了能源费用指标，导致单位电耗和单位能耗有所增加；其正面作用是有效缩小了多台泵组累计运行时间差，便于维护计划的制定并延长泵组的使用年限.

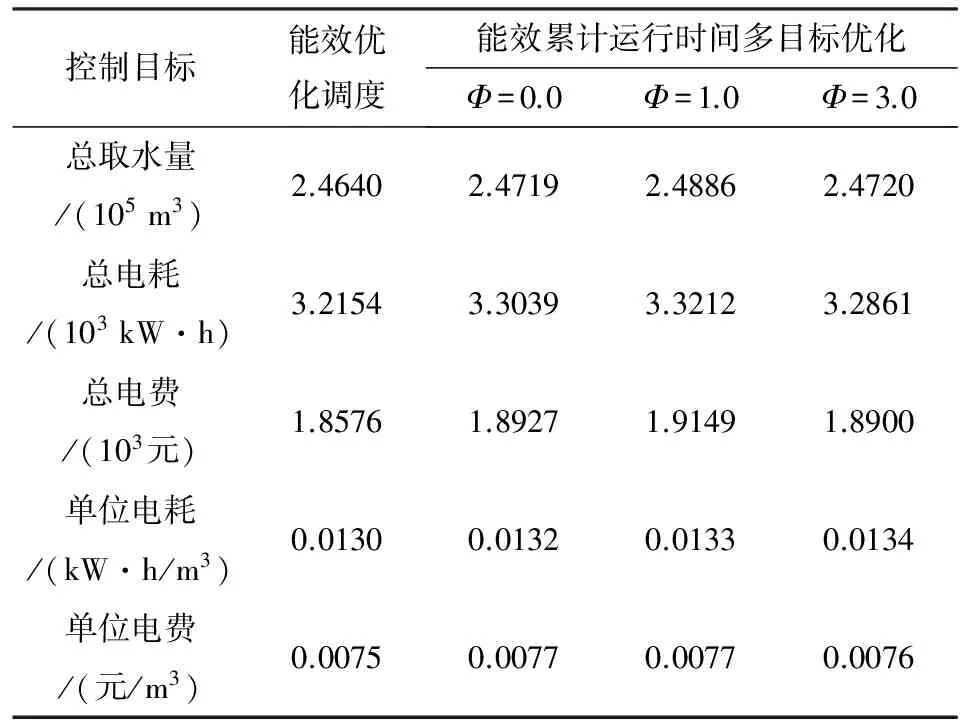
表1 优化性能统计

4 结语

均衡各泵组的累计运行时间与泵站维护及泵组寿命密切相关，实际上也是一种提升泵站性能效率的有效手段.然而，当前取水泵站优化调度研究大多只针对能源效率开展.本文以能源费用及累计运行时间差为目标函数提出了泵站多目标优化调度方法.并针对多目标优化问题提出了基于PSO的求解方法.水厂取水泵站实例研究表明了能效累计运行时间多目标优化调度方法的有效性.另外，通过平衡系数Φ可以调整多个目标的权重，获得不同的调度目标，以满足多场合的应用需求.另外，本文建立的泵站优化问题及其求解方法都无需复杂计算，可以方便地在当前控制设备或采用独立的工业控制计算机(IPC)中实现，具有较好的现场应用性和推广能力.

[1]Xia X,Zhang J. Control systems and energy efficiency from the POET perspective[C]//IFAC. Conference on Control Methodologies and Technology for Energy Efficiency. Vilamoura:IFAC,2010.

[2]Zhang J,Xia X,Alexander D. Demand side optimal strategy for voluntary load shedding[C] //IASTED.The second IASTED Africa conference on power and energy system. Gaborone:IASTED,2008.

[3]Barán B,Von Lücken C,Sotelo A. Multi-objective pump scheduling optimisation using evolutionary strategies[J]. Advances in Engineering Software. 2005,36(1): 39-47.

[4]Beckwith S P,Wong K P. A genetic algorithm approach for electric pump scheduling in water supply systems[C] //IEEE. International Conference on Evolutionary Computation. Perth:IEEE,1996.

[5]Moreno M A,Planells P,Córcoles J I,et al. Development of a new methodology to obtain the characteristic pump curves that minimize the total cost at pumping stations[J]. Biosystems Egineering,2009,102(1): 95-105.

[6]Moreno S A,Carrión P A,Planells P,et al. Measurement and improvement of the energy efficiency at pumping stations[J]. Biosystems Engineering,2007,98(4): 479-486.

[7]Lertpalangsuntia N,Chana C W,Masonb R,et al. A toolset for construction of hybrid intelligent forecasting systems: application for water demand prediction [J]. Artificial Intelligence in Engineering,1999,13(1): 21-42.

[8]Zhou S L,McMahan T A,Walton A,et al. Forecasting operational demand for an urban water supply zone[J]. Journal of Hydrology,2002,259: 189-202.

[9]专祥涛,李明龙. 基于移峰填谷的排水泵站优化调度研究[J]. 武汉大学学报:工学版,2011,44(6):773-778.

[10]Zhang He,Xia Xiaohua,Zhang Jiangfeng. Optimal sizing and operation of pumping systems to achieve energy efficiency and load shifting[J].Electric Power Systems Research,2012,86(5): 41-50.

[11]van Staden Adam Jacobus,Zhang Jiangfeng,Xia Xiaohua. A model predictive control strategy for load shifting in a water pumping scheme with maximum demand charges[J]. Applied Energy,2011,88(12): 4785-4794.

[12]Tang Yuling,Zhang Shirong. A model predictive control approach to operational efficiency of intake pump stations[C]//ECE.International Conference on Electrical and Control Engineering. Wuhan:ECE,2010.

[13]张礼华,程吉林,张仁田,等. 基于试验-整数规划方法的泵站多机组变速优化[J]. 农业工程学报,2011,27(5):156-159.

[14]Sychta L. System for optimising pump station control[J]. World Pumps,2004,449: 45-48.

[15]Sychta L. System for optimising pump station control-Part-II[J]. World Pumps,2004,454: 32-34.

[16]Shi Yuhui,Eberhart Russell. A modified particle swarm optimizer[C]//IEEE. World Congress on Computational Intelligence. Alaska:IEEE,1998.

[17]杨 维,李歧强. 粒子群优化算法综述[J]. 中国工程科学,2004,6(5): 87-93.