带有红树林自然保护区的渔业资源的离散动力学模型的局部分析
顾恩国,陈 博,张梅娜
(中南民族大学 数学与统计学学院,武汉 430074)
红树林是指生长在热带、亚热带低能海岸潮间带上部,受周期性潮水浸淹,以红树植物为主体的常绿灌木或乔木组成的潮滩湿地木本生物群落.它生长于陆地与海洋交界带的滩涂浅滩,是陆地向海洋过渡的特殊生态系,具有维护海岸潮间带的生物多样性、防风消浪、促淤造陆、固岸护堤、净化海水和空气等生态功能,也具有很高的经济价值和社会价值,素有“海洋卫士”之称,我国的红树林主要分布于广西、广东、海南、台湾、福建和浙江南部沿岸.红树林生态系统具有复杂的碎屑食物链[1]和海洋动物良好的生长发育环境[2,3],是近海渔业和滩涂养殖业的重要场所之一,它在全球保护生物多样性、保护湿地和保证资源可持续利用中起着重要作用.改革开放以来,一方面围塘养殖、城市化、港口码头建设、乱砍乱伐及工业区的开发等危害红树林的行为层出不穷;另一方面红树林区群众又在过度利用红树林区丰富的渔业资源,非常不利于红树林生态系统的保护.
关于海洋渔业资源可持续利用的问题,国内外很多学者建立了大量模型[4-6],但针对带有红树林自然保护区的海洋渔业资源可持续利用的研究至今很少见.本文主要运用离散动力学知识研究捕捞力度对带有红树林自然保护区的海洋渔业资源可持续利用的影响,研究发现合理控制捕捞力度可以实现对红树林生态系统的保护.鉴于红树林生态系统为幼鱼的繁殖和生长提供了极为有利的场所[7],我们假定鱼群仅在红树林区进行繁殖(红树林之外的繁殖活动较小我们忽略不计),并且在该区域禁止捕捞,建立了渔业资源储量的离散动力学模型,来描述鱼群密度随时间演化的规律,给出保证渔业资源的可持续利用的条件,研究结果可以为资源管理者提供理论参考.
1 模型建立
本文主要考虑带有红树林自然保护区的海洋渔业资源,红树林区和捕捞区鱼群的密度分别为x1,x2,捕捞力度为E,它依赖于假设所有渔船的捕捞技术、作业渔船的数量和作业时间确定.用s表示红树林区占整个区域的比例(0 (1) (2) 我们可以将(2)式写成如下的映射动力系统形式 这里“′”表示时间增加一个单位算子.下面求系统(3)的不动点,根据平衡点的定义,系统(3)的平衡点应满足x′=x,y′=y,即: 系统有两个平衡点A0(0,0),A1(x*,y*),这里 考虑模型本身的意义,我们仅考虑正平衡点,因此A1应满足x*>0,y*>0.于是得到下面结论. 命题1 ① 当sr>σ时,系统(3)有正平衡点A1; 本文主要对第一种情况下带有红树林生态系统的渔业资源的离散动力学模型进行分析. 本节我们假设σ (ii)在正平衡点A1(x*,y*)处, P(-1)=F(Eq)=A+f(Eq), 所以此时系统(3)的正不动点不可能产生Neimark分叉. 综合上面的分析,可以得到关于正不动点A1(x*,y*)的稳定性和局部分叉定理1. 1)系统(3)在正平衡点处不可能产生fold分叉; 2)当s>σ且s+σ<1时,系统(3)在正平衡点处不可能产生Neimark分叉; 为了分析捕捞力度对资源可持续利用的影响,我们给出系统(3)关于捕捞力度E的分叉图.图1中初始渔业资源x0=0.24,y0=0.06,系统参数为σ=0.31,s=0.41,q=0.7,r=0.97,蓝色虚线表示红树林区渔业资源的分叉图,红色实曲线表示捕捞区渔业资源的分叉图.由图1可知,当0 图1 系统(3)关于参数r=0.97,σ=0.31,s=0.41,q=0.7随捕捞力度E变化的分叉图 取参数为r=0.97,σ=0.31,s=0.41,q=0.7,不动点A1(x*,y*)=(0.1893,0.0842),当E≈1.676时,P(-1)=0,为了回答在此临界状态平衡点A1的局部稳定性,需要用到中心流形定理. 对系统(3)作坐标平移变换得: (4) 其矩阵形式为: 令 设中心流形为Mc={(u,v)∈R2|v=h(u),h(0)=0,h′(0)=0,|u|<δ},h(u)=b1u2+b2u3+o(u4),则h(mu+f(u,h(u)))-nh(u)-g(u,h(u))=0,其中m=0.6196,n=-1,进而有: 其中f1(u)=-u+0.7060u2-0.1647u3+o(u4),所以h(u)为稳定流形,则平衡点A1在E=1.676处局部稳定. 本文研究了带有红树林自然保护区的海洋渔业资源可持续利用问题,假设鱼群仅在红树林自然保护区进行繁殖,并且仅在非保护区域进行捕捞,建立了渔业资源储量的离散动力学模型,并对模型进行了非线性动力学的局部分叉的分析,讨论了正平衡点的存在性、局部分叉和稳定性,并且应用中心流形定理讨论了系统有一个特征值为-1时的稳定性问题.我们发现带有红树林区的渔业资源相对比较容易达到稳定状态,但当捕捞力度过大(E>1.67)时,系统非常敏感,资源很容易就枯竭.因此要保证红树林区渔业资源的可持续利用,必须合理控制捕捞力度,这对于政府部门有一定的参考价值. 本文仅对系统进行了非线性动力学的局部分叉的分析,没有对系统的可行域进行全局分析,不清楚系统稳定性对捕捞力度变化的抗干扰能力,不可行吸引域中资源的枯竭年限也无法预知,这将在后文中继续研究. [1]Odum E P,Heald R J. Detritus based food web of an estuarine mangrove community[M]. New York: Academic Press,1975: 256- 286. [2]Thayer G W,Colby D R,Hettler W F. Utilization of the red mangrove prop root habitat by fishes in south Florida [J]. Marine Ecology Progress Series,1987,35:25-38. [3]Robertson A I,Duke N C. Mangroves as nursery sites: comparisons of the abundance and species composition of fish and crustacean in magroves and the other near shore habitats in tropical Australia [J]. Marine Biology,1987,96:193-205. [4]Bischi G I,Kopel M,Szidarovszky F.Expectation-stock dynamics in multiagent fisheries [J]. Annals of Operations Research,2005,137:299-300. [5]Kar T K,Matsuda H. A bioeconomic model of a single-species fishery with a marine reserve [J]. Journal of Environmental Management,2008,86: 171-180. [6]Gu Enguo,Rung J. On some global bifurcations of domains of feasible trajectories: analysis of recurrence equations [J]. International Journal of Bifurcation and Chaos,2005,14 (5):1625-1639. [7]何斌源,范航清.广西英罗港红树林潮沟鱼类多样性季节动态研究[J].生物多样性,2002,10(2): 175-180.2 正平衡点的存在性

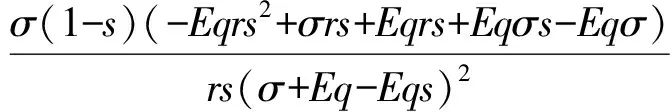
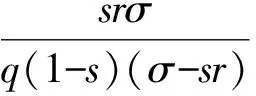
3 非负平衡点的局部稳定性和分叉


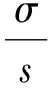

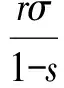
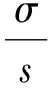
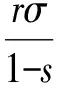
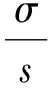

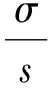
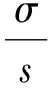

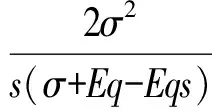







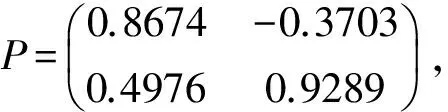


4 结语和展望

