含有奇异项的退缩抛物型方程解的整体存在性与有限时刻猝灭性
孙仁斌
(中南民族大学 数学与统计学学院,武汉 430074)
对于含有奇性的半线性抛物型方程的初边值问题:

本文讨论如下含有奇性的退缩抛物型方程初边值问题:
(1)

本文将对Ω为N维区域的情形进行讨论.
1 解的局部存在性
由于当u=0时,问题(1)中的方程为退缩,经典的抛物方程理论并不能直接给出解的存在性.而对解的存在性的讨论,我们也不需要针对问题的古典解,而只需要问题的弱解,为此先给出问题(1)中方程弱解的定义.
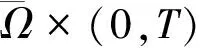
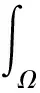

f(u(x,t))φ(x,t)]dxdt.
(2)
则称u(x,t)为方程的弱解.
如果对任意T>0,方程的弱解都存在,则称弱解为整体存在.
关于退缩抛物型方程弱解的局部存在性,有多种方法可以得到[9,10],在此给出其中一种方法的主要步骤.
对k=1,2,…,考虑如下抛物型方程的初边值问题:


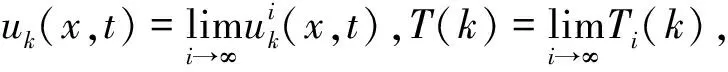
可以证明,如果k1>k2,则T(k1)>T(k2),且在Ω×(0,T(k2))内有uk1(x,t)>uk2(x,t).

定理1 设u0(x)>0,u0(x)∈L∞(Ω),则存在T>0,使问题(1)存在非负的弱解u(x,t)定义在Ω×(0,T)上.
为了得到后面的整体存在性定理,我们需要利用上、下解及其相关的结论.

(4)
则称u(x,t)为问题(1)的一个下解,如果将上面的不等式改变方向,就称u(x,t)为问题(1)的一个上解.
对于弱解,与古典解一样,也有如下的比较原理和存在唯一性定理[12].


2 解的整体存在性



(5)

(6)

(7)
(8)

定理4 设正常数d满足(8)式,区域Ω充分小,其直径满足(7)式,则问题(1)存在整体解.
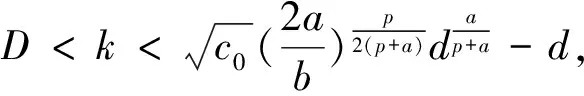
3 解在有限时刻的猝灭性
而对于退缩抛物型方程古典解的存在性,也有多种方法可以得到[13],在此省略.为明确起见,我们先给出问题(1)古典解猝灭的定义.


(9)
设λ1与φ(x)是如下特征值问题的第一特征值与相应的特征函数:
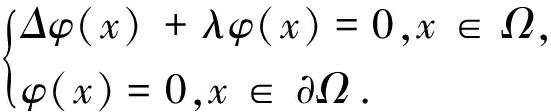
(10)
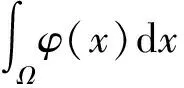
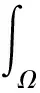



(11)
我们知道,特征值λ1与区域Ω有关,Ω越大,λ1越小,根据上面的分析,可以得到定理5.
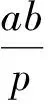

(12)
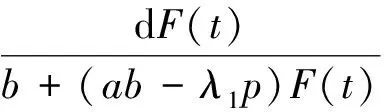


为了证明(12)式的前一不等式,考虑如下初值问题:

[1] Guo J S.On the quenching behavior of the solution of a semilinear parabolic equation[J].J Math Anal Appl,1990,151:58-79.
[2] Dai Q Y,Gu Y G.A short note on quenching phenomena for semilinear parabolic equations[J]. J Differential Equations,1997,137:240-250.
[3] Salin T.On quenching with logarithmic singularity[J].Nonlinear Analysis,2003,52:261-289.
[4] Bertdch M,Ughi M.Positivity peopertics of viscosity solutions of a degenerate parabolic equation[J].Nonlinear Analysis,1990,14:571-592.
[5] Friedman A,Mcleod J B. Blowup of solutions of nonlinear degenerate parabolic equations[J]. Arch Rational Mech Anal,1987,96:55-80.
[6] Chen H W. Analysis of blowup for a nonlinear degenerate parabolic equations[J]. J Mathemetical Analysis and Applications,1995,192:180-193.
[7] Chen Y P,Liu Q L,Xie C H.Blow-up for degenerate parabolic equations with nonlocal source[J].Proceedings of the American Mathematical Society,2004,132:135-145.
[8] Winkler M.Quenching phenomena in strongly degenerate diffusion equations with strong absorption[J]. J Math Anal Appl,2003,288:481-504.
[9] Anderson J R.Local existence and uniqueness of solutions of degenerate parabolic equations [J].Comm Partial Differential Equations,1991,16:105-143.
[10] Aronson D G,Crandall M,Peletier L A.Stabilization of solutions of a degenerate nonlinear diffusion problem[J].Nonlinear Analysis,1982,6:1001-1022.
[11] Pao C V.Nonlinear parabolic and elliptic equations[M].New York:Plenum Press,1992.
[12] Anderson J R,Deng K.Global existence for degenerate parabolic equations with a non-local forcing[J].Methods Appl Sci,1997,20:1069-1087.
[13] Galaktionov V A,Kurdyumov S P,Samarskii A A.A parabolic system of quasilinear equations [J].Differential Equations,1985,21:1049-1062.

