带有保护区的单一渔业资源的离散动力学模型分析
顾恩国,李晓东,向 蕾,李远平
(中南民族大学 数学与统计学学院,武汉 430074)
公共渔业资源是人类重要的食物来源,随着社会的发展和人口数量的急速增长,对公共渔业资源的过度捕捞已严重影响到其再生能力,进而影响了人类对公共渔业资源的可持续利用[1,2].因此,如何做到既满足人类对渔业资源的合理需求,又保证公共渔业资源的持续再生能力,越来越引起人们的重视.对于公共渔业资源的可持续利用问题,国内外的学者建立了大量模型[3-6],但考虑保护区面积变化对渔业资源可持续利用的影响这方面的研究还很少.针对带有保护区的公共渔业资源,运用离散动力学知识研究保护区面积比例和捕捞力度变化对渔业资源储量的影响,无论是在学术上还是渔业资源管理上都具有重要的意义.因此,本文假设渔业资源为单一渔业资源,并分属于保护区和捕捞区,鱼在两个区域之间按照一定的迁移率自由迁移.在此条件下构造离散动力学模型,并以此模型来研究渔业资源保持可持续再生能力的条件,包括保护区面积比例及捕捞力度对渔业资源最终演化产生的影响,其结果能够为渔业资源管理提供理论参考.
1 模型的建立
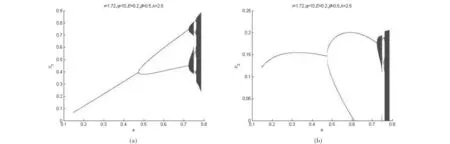
本文考虑构成单一渔业资源区域的保护区和捕捞区内鱼的数量在t时刻分别为X1(t)和X2(t),两个区域内其自然增长率均为r,鱼在两个区域之间的迁移率为β,保护区占整个渔业资源区域的面积比例为s(0 (1) (2) 此时有0≤X1(t)≤1,0≤X2(t)≤1. 根据平衡点的定义,系统(2)的平衡点是下面这个以X1和X2为未知元的二元二次方程组的解: (3) 即是以下两条凸抛物线的交点: (4) 首先,原点X0=(0,0)显然是系统(2)的平衡点.关于正平衡点的存在性,我们有下面3个命题成立(因篇幅原因证明过程略). 差分方程(2)的Jacobian矩阵是: (5) 通过计算所得Jacobian矩阵的特征值λ1,λ2得: (6) (7) 其中M=(qEs(1-s)-2r(1-s)X1+2rsX2-σ+2σs)2+4σ2s(1-s).由M>0知,λ1,λ2均为实数,且有λ1<λ2. 对平衡点X0=(0,0)的稳定性,在没有捕捞行为(E=0)的情况下,λ2=1+r>1,此时X0=(0,0)是不稳定的. 这一结果不仅在动力学的研究上非常有意义,而且在渔业资源的实际管理上也非常有意义.如果我们能够找到一个E的区间,在这个区间里,系统(2)的Jacobian矩阵的两个特征值的模都小于1,此时正平衡点具有稳定性.这就是说,在资源管理上,我们能够通过控制在捕捞区的捕捞力度实现对渔业资源的持续利用. 图1 系统(2)关于参数r=1.98,s=0.46,q=10,β=0.3125,k=2.5随捕捞力度E变化的分叉图 图2 系统(2)关于参数r=1.72,q=10,E=0.2,β=0.5,k=2.5随保护区面积比例s变化的分叉图 (8) (9) 图3 系统(2)关于参数r=1.72,q=10,E=0.2,β=0.5,k=2.5随着保护区面积比例s变化的可行域 本文提出了带有保护区的单一渔业资源的离散动力学模型,并对模型进行了非线性动力学分析,讨论了正平衡点的存在性、稳定性及局部分叉,并对正平衡态进行了全局分析.对于满足人类对渔业资源的可持续利用的问题,本文给出了较好的回答.我们发现,保护区面积和捕捞力度对公共渔业资源的可持续再生能力具有显著的影响,当捕捞力度E过大时,捕捞区的渔业资源可能枯竭(当E>0.307时,资源稳定到负的平衡态);当保护区面积s过大或者过小时,都不利于人类对渔业资源的可持续利用,当s在一定范围(如图3中的0.065 [1] Food and Agriculture Organization. The state of world fisheries and aquaculture[R]. Sofia: FAO,2010: 3-12. [2] Garcia S M,Grainger R J R. Gloom and doom? The future of marine capture fisheries[J]. Philosophical Transactions of the Royal Society B: Biological Sciences,2005,360: 21-46. [3] Clark C W. Mathematical bioeconomics: the optimal management of renewable resources[M]. New York:Wilery,1976. [4] Bischi G I,Kopel M,Szidarovszky F. Expectation-stock dynamics in multi-agent fisheries[J]. Annals of Operations Research,2005,137(1): 299-329. [5] Kar T K,Matsuda H. A bioeconomic model of a single-species fishery with a marine reserve[J]. Journal of Environmental Management,2008,86: 171-180. [6] Bischi G I,Lamantia F. Harvesting dynamics in protected and unprotected areas[J]. Journal of Economic Behavior & Organization,2007,62:348-370. [7] Saber N E. Discrete chaos[M]. New York: Chapman & Hall/CRC,2000: 180-234. [8] Gu Enguo,Ruan Jiong. On some global bifurcations of domains of feasible trajectories: analysis of recurrence equations[J]. International Journal of Bifurcation and Chaos,2005,15(5): 1625-1639. [9] Gu Enguo,Huang Yibing. Global bifurcations of domains of feasible trajectories: analysis of a predator-prey model[J]. International Journal of Bifurcation and Chaos,2006,16(9): 2601-2613.2 正平衡点的存在性



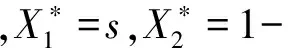

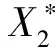
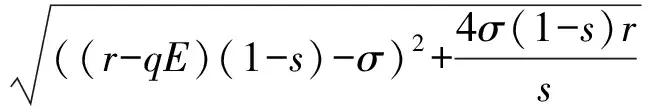
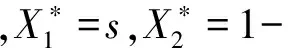
3 正平衡点的局部稳定性及分叉






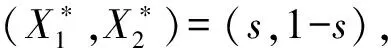





4 正平衡点的全局分析



5 结语

