基于变分稀疏贝叶斯学习的频谱检测方法
朱翠涛,杨 凡
(中南民族大学 电子信息工程学院,武汉 430074)
在认知无线电网络中,由于频谱利用率低而导致认知用户接收的宽带信号在频域具有稀疏性,因此,人们将压缩感知技术用于频谱检测,降低对宽带信号采样的压力[1].大部分文献[2,3]利用压缩感知技术,先恢复信号,再进行谱的估计,这样导致检测算法的复杂度增加.文献[4]提出了稀疏贝叶斯方法直接利用观测值进行相关参数的估计.基于相关向量机的稀疏贝叶斯模型不仅能够估计出授权基站的位置而且也能测出正在通信授权用户的个数.但是,基于相关向量机[5]的稀疏贝叶斯模型在计算过程中收敛速度很慢.而且,当权值的先验分布服从高斯分布时,单个的稀疏参数可能会在闭合式中估计[6].
针对以上情况,我们提出了基于变分稀疏贝叶斯学习模型的方法.该方法用概率分布估计未知变量.这样就避免了参数闭合式估计的情况.而且,对于难以求解的函数,变分学习方法能够分解为几个简单函数来逼近,降低了计算难度.变分方法在推导图示模型时还能够提供一致的推导框架.
1 系统模型
系统模型如图1所示,设在Np×Np的区域内,有N个认知用户(简称CR用户)、Mp个授权用户(简称PU用户)和一个融合中心.CR用户出现的位置用笛卡尔坐标表示为:
X=(x1,x2,x3,…,xn)Txi=(xix,xiy).

图1 系统模型
该系统模型中,无线电功率传播模型为[7]:

(1)
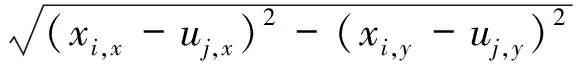
检测期间,CR用户接收到的信号表示为:
t=ts+n,
(2)
式(2)中,ts=(t1,t2,…,tN)T,n=(ε1,ε2,…,εn)T表示信号传输过程中受到的阴影效应,εi表示均值为0,方差σ2为的高斯变量.
根据压缩感知理论,ts可以表示成转换矩阵Φ(X)与待测未知信号w的乘积,即ts=Φ(X)w.那么观测向量可表示为:
t=Φ(X)w+n,
(3)
其中w=[w1,w2,…,wM],
(4)
方便起见,把矩阵(4)每列简写为φj(X)=(φj(x1),(φj(x2),…,(φj(xN))T.根据前面已经给出的无线电功率传播模型(1),本文算法采用以下函数作为之后的贝叶斯推理的基函数[4]:
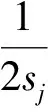
(5)
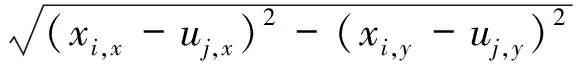
根据公式(3)、矩阵(4)可推算出观测向量t中的每个元素ti的表达式,即数学模型如下:
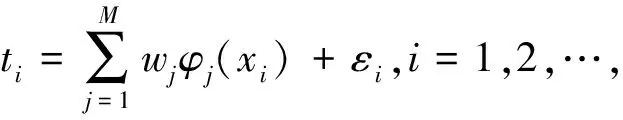
(6)
式(6)是一个线性回归模型.本文采用变分稀疏贝叶斯算法(简称VSBL算法)来求解.VSBL算法并未对边缘似然函数对数函数直接求解而是通过变分逼近的方法求解出稀疏因子w.
2 变分稀疏贝叶斯及推理
2.1 变分稀疏贝叶斯模型
频谱检测重构数学模型如公式(6)所示.设CR用户采样样本数据是独立同分布的数据集合X={xi},t={ti}.假定εi为高斯白噪声:εi~N(0,τ-1),那么观测变量的似然函数可表示为[5]:
p(ti|xi,w,τ)=N(ti|y(xi,w),τ-1),
其中:

那么似然函数可以表示为:

如果直接最大化似然函数来估计w,会导致模型过学习.为了克服此问题,我们假设稀疏参数wm服从均值为0方差为αm的高斯分布,即:

(7)
公式(7)中,αm为超参数,它决定稀疏因子w的稀疏性.同时为超参数αm引入一个Gamma分布:
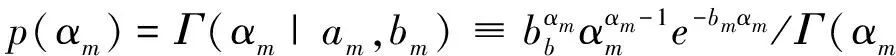
(8)
式(8)中,Γ(αm)是一个Gamma函数.由于εi噪声协方差为变量,所以同样为其引入以下分布:
p(τ)=Γ(τ|c,d).
由于不存在先验知识,在初始化时,我们设定am=bm=c=d=10-6.根据以上假设,变分稀疏贝叶斯概率模型直观图如图2所示.
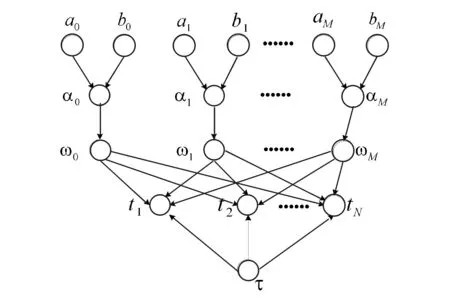
图2 概率模型直观图
2.2 变分稀疏贝叶斯推理
若已知模型参数的先验概率是p(w,α,τ),那么后验概率可表示为:
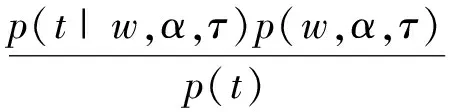
若用稀疏贝叶斯求解后验概率,则先将后验概率分解为:
p(w,α,τ|t)=p(w|t,α,τ)p(α,τ|t),
然后再用积分求解p(w|t,α,τ),算法实现比较复杂.本文采用变分稀疏贝叶斯的方法对后验概率进行逼近,即:
p(w,α,τ|t)≈Q(w,α,τ).
(9)
由于变量参数w,α,τ对于Q分布是相互独立的,那么:
Q(w,α,τ)=Qw(w)Qα(α)Qτ(τ).
从文献[8]可知各个参数服从以下分布:
Qw=N(w|mw,∑w),
其中:
(10)
(11)

(12)
(13)
(14)
(15)
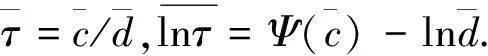
(16)
公式(15)、(16)中Ψ函数定义为:
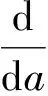
公式(9)的证明如下:
根据贝叶斯公式,观测数据的边缘概率表示为公式:

(17)
依据变分理论,引入一个关于变量w,α,τ的Q分布.为了保证公式(17)两边等式成立,公式(17)可变换为:

(18)
然后对公式(18)两边取对数:

(19)
设定∭Q(w,α,τ)dwdαdτ积分等于1.公式(19)可以转化为:


简记:
ln(p(t))=L(Q(w,α,τ))+KL(Q(w,α,τ)‖p(w,α,τ|t)).
(20)
式(20)中KL(Q(w,α,τ)‖p(w,α,τ|t))≥0,那么对于ln(p(t))来说L(Q(w,α,τ)是下界值.ln(p(t))数值一定时KL(Q(w,α,τ)‖p(w,α,τ|t))值越小,L(Q(w,α,τ)值越大,函数越收敛.因此,Q(w,α,τ)与p(w,α,τ|t)越接近越好,即:
p(w,α,τ|t)≈Q(w,α,τ),
同时用L(Q(w,α,τ))作为算法的收敛条件其公式如下[8]:
L(Q(w,α,τ)=
(21)
3 问题求解及算法实现过程
在整个算法实现过程中,由于uj与sj更新速度慢.所以,超参数α与噪声方差τ迭代更新一次,uj与sj将更新P次.在处理大量数据时,为了减轻计算负担,本文先计算稀疏参数w,然后根据设定的阈值η,当稀疏因子wm<η时,删除wm及其所对应的基函数.最后在w,α,τ都给定的前提下,我们用梯度下降法对PU用户定位[4].即:
(22)
式(22)中k为迭代次数,Q=-L,δ为学习步长.其中:

(23)

(24)
(25)

算法的实现过程如下:
(1)根据公式(5)初始化M个基函数,创建基函数矩阵Φ.

(3)其次由步骤2得到的结果及根据公式(10)计算并mw、∑w由公式(21)计算收敛条件L(K)的值.


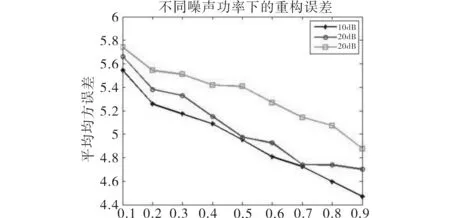
(6)然后再用梯度下降法对PU用户进行定位.根据公式(22)更新uj、sj,并且根据公式(10)估计mw、∑w.再次计算本次迭代之后收敛条件L(K)的数值.若L(K) 实验(1)采样率=0.9时本算法对频谱功率传播图进行重构.采样率计算公式如下: Measurement rate=N/Np×Np. 重构效果如图3所示. 图3 变分稀疏贝叶斯重构图与原图比较 图3可看出,采用变分稀疏贝叶斯学习方法能实现很好的重构. 实验(2)分别设定噪声功率为10dB、20dB、30dB,比较不同噪声功率对功率图重构的影响.性能比较图如图4所示. 采样率(N/Np×Np) 噪声功率越大,对信号干扰越强,重构信号时造成的误差越大.图4可看出,在相同采样率下,噪声功率越大均方误差越大. 实验(3)比较VSBL算法与SBL算法对功率传播图重构时造成的均方误差,如图5所示. 采样率(N/Np×Np) 从图5可以看出VSBL重构均方误差比SBL的均方误差要低. 实验(4)在不同的采样率下,比较PU用户真实位置与预测位置之间测均方误差.如图6所示. 采样率(N/Np×Np) 从图6可看出,随着采样率的提高,PU用户真实位置与预测位置之间的均方误差变小. 本文提出的基于变分稀疏贝叶斯频谱感知算法直接利用压缩测量数据对授权用户的位置、个数以及功率传播图进行估计和定位,克服由于采用压缩感知带来的算法复杂性.且在先验知识未知的情况下,利用变分稀疏贝叶斯求解稀疏权值,用简单函数因子逼近复杂函数的方法降低边缘似然函数的计算难度.下一步重点研究分布式合作压缩频谱感知算法的一般框架,分析其收敛性质与通信负担. [1] 石光明,刘丹华,高大化,等. 压缩感知理论及其研究进展[J]. 电子学报,2009,37(5): 1070-1081. [2] Tian Z,Giannakis G. Compressed sensing for wideband cognitive radios[C]//IEEE.IEEE International Conference.Honolulu:IEEE,2007: 1357-1360. [3] Ji S,Xue Y,Carin L. Bayesian compressive sensing [J]. IEEE Trans on Signal Processing,2008,56(6): 2346-2356. [4] Tina Huang D-H,Wu S-H,Wang P-H . Cooperative spectrum sensing and locationing: a sparse bayesian learning approach[C]//GTC.Proc Global Telecommunications Conference.New York:GTC,2010: 1-5. [5] Tipping M E. Sparse Bayesian learning and the relevance vector machine[J]. Journal of Machine Learning Research,2001,1: 211-244. [6] Shutin D,Buchgraber T,Kulkarni SR,et al.Fast variational sparse Bayesian learning with automatic relevance determination[J].IEEE Trans on Signal Process,2011,59(12):6257-6261. [7] Rappaport T S . Wireless communications: principles and practice[M]. 2nd ed. PTR: Prentice Hall,2002. [8] Bishop C M,Tipping M E. Variational relevance vector machines[C]//CUAI. Proceedings of the 16th Conference on Uncertainty in Artificial Intelligence.New York:CUAI,2000: 46-53.
4 试验结果及分析
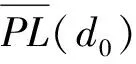



5 结束语

