基于平顺性某型汽车悬架的优化选择

朱从云，朱亚伟，姜春英，史建茹，聂建军

（中原工学院，郑州450007）

随着汽车产业的竞争越来越激烈，人们对汽车的要求从最初具有良好的动力性和经济性逐渐发展为具有良好的平顺性和操纵稳定性［1－2］.汽车的平顺性主要是指汽车在行驶过程中产生的振动和冲击对乘员舒适性的影响保持在一定界限之内，因此平顺性主要是根据乘员主观感觉的舒适性来评价的，它是现代高速汽车的主要性能之一.路面不平是汽车振动的基本输入，并通过悬架系统将振动传递给人体，因而悬架系统的主要参数固有频率f0和阻尼比ζ对汽车平顺性具有决定性影响.本文以一种大众款的城市SUV为例，探讨汽车悬架参数的优化选择.

1 汽车平顺性的评价指标

研究汽车平顺性，常用车身振动的频率和振动加速度作为评价指标.为了保证汽车具有良好的平顺性，车身振动的固有频率应为人体步行时所习惯的1～1.6Hz，振动加速度的极限值为2～3m／s2.当把振动系统的“输出”作为优化目标时，通常要综合考虑车轮与路面间的动载和悬架刚度的动挠度，它们分别影响着汽车的行驶安全性和撞击悬架限位的概率.

研究汽车平顺性，将汽车视为线性振动系统.如图1所示，将汽车简化为三自由度双轴振动模型.路面不平度和车速视为汽车振动系统的“输入”，“输入”经过轮胎、悬架座椅等弹性和阻尼元件以及悬挂、非悬挂质量构成振动系统的传递，得到的“输出”是人体的加速度.

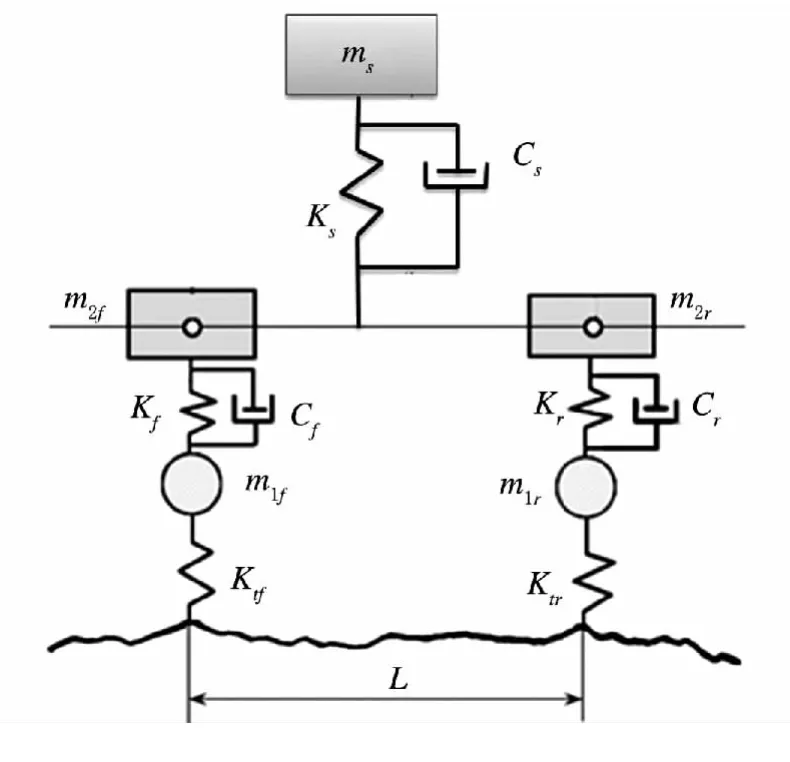
图1 三自由度双轴汽车振动模型

对于线性系统来说，如果输入是正态分布的，输出也必然是正态分布的.大量的测量表明，路面的随机输入和汽车的振动响应都基本上符合正态分布.这样，汽车振动响应量的标准差与其概率分布之间存在着正态分布的简单关系.

当车轮与地面间的动载Fd与车轮作用于路面的静载G大小相等且方向相反时，车轮作用于路面的垂直载荷等于零.此时，车轮会跳离路面，将失去纵向和侧向附着力，使行驶安全性恶化.通常取G＝3σFd，此时参数λ＝3，概率P＝0.3%，其中σFd为相对动载的均方根值.车轮与地面间的动载Fd的方向是上、下交变的，因此车轮跳离地面的概率为0.15%.同上，为了将汽车撞击限位的概率控制在0.3%之内，悬架动挠度应不超过限位行程fd的1／3［3－4］.

2 汽车振动响应量的计算

研究汽车的平顺性，将“人体—座椅”振动系统附加在双轴振动系统之上，就构成了计算人体加速度所需的三自由度振动系统.评价汽车平顺性的另外两个指标相对动载Fd和悬架动挠度fd需在双质量系统模型中进行研究.由于“人体—座椅”振动系统是固定不变的，所以在三自自由度振动系统中，车身幅频特性和人体幅频特性变化趋势一致，故下文主要探讨人体加速度的幅频特性随着悬架参数变化而受到的影响.为了将相对动载、悬架动挠度和人体加速度放在同一双质量系统中进行研究，可以用车身加速度的幅频特性代替人体加速度的幅频特性，具体计算过程如下：

（1）“人体—座椅”振动系统的幅频特性：

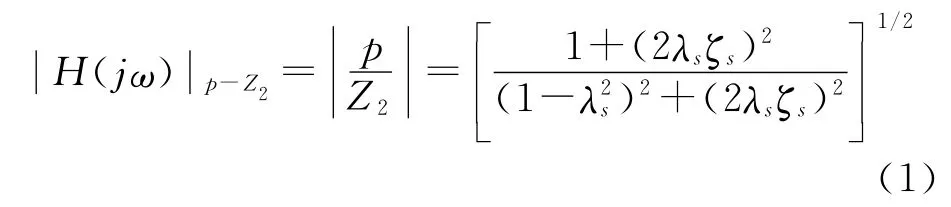
（2）双质量振动系统的幅频特性：

车身加速度¨Z2对˙q的幅频特性为

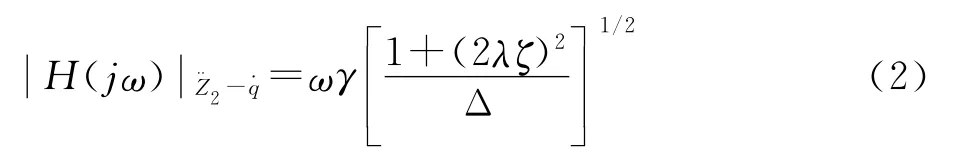
相对动载Fd／G对q·的频率响应函数为

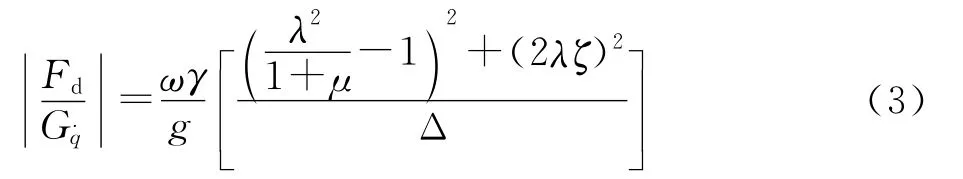
动载fd对q·的频率响应函数为

（3）双轴振动系统的幅频特性：

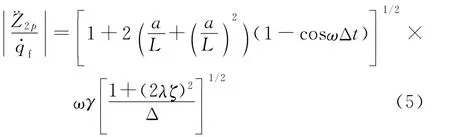
（4）三质量振动系统的幅频特性：

车身上任意一点（距前轴距离为a）的人体加速度对q·的幅频特性为

其中：q·为路面不平度函数的导数；

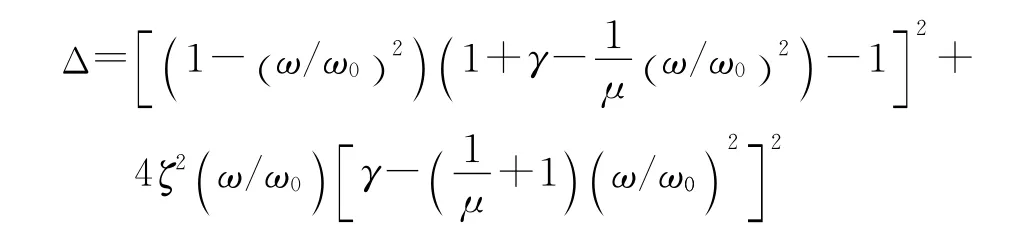
振动响应的功率谱密度Gx（f）与路面速度输入的功率谱密度G˙q（f）有如下关系：

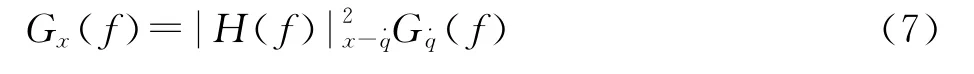
由于振动响应量取正负值的概率相同，所以其均值近似为零.这些量的统计特征值方差等于均方值，并可由功率谱密度对频率积分求得：

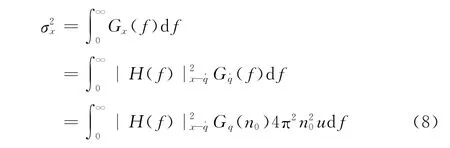
人体加速度、悬架动挠度和相对动载的标准差均可代入上式求得［2］.

3 固有频率和阻尼比对平顺性的影响

3.1 车身固有频率f0的影响

图2（a）—2（c）为f0分别取0.5Hz、1Hz、2Hz，其他参数保持不变时，振动响应量¨Z2、fd和Fd／G 对q·的幅频特性.

从图2（a）－2（c）中可以看出，3个振动响应量对f0的变化都是很敏感的.随着车身固有频率的增加，悬 架动挠度fd对˙q的幅频特性显著降低，但¨Z2对˙q越大则动挠度越小，所以悬架动挠度随车身固有频率的增加而降低.Fd／G对˙q的幅频特性与¨Z 对˙q的幅频特性变化趋势完全一样.

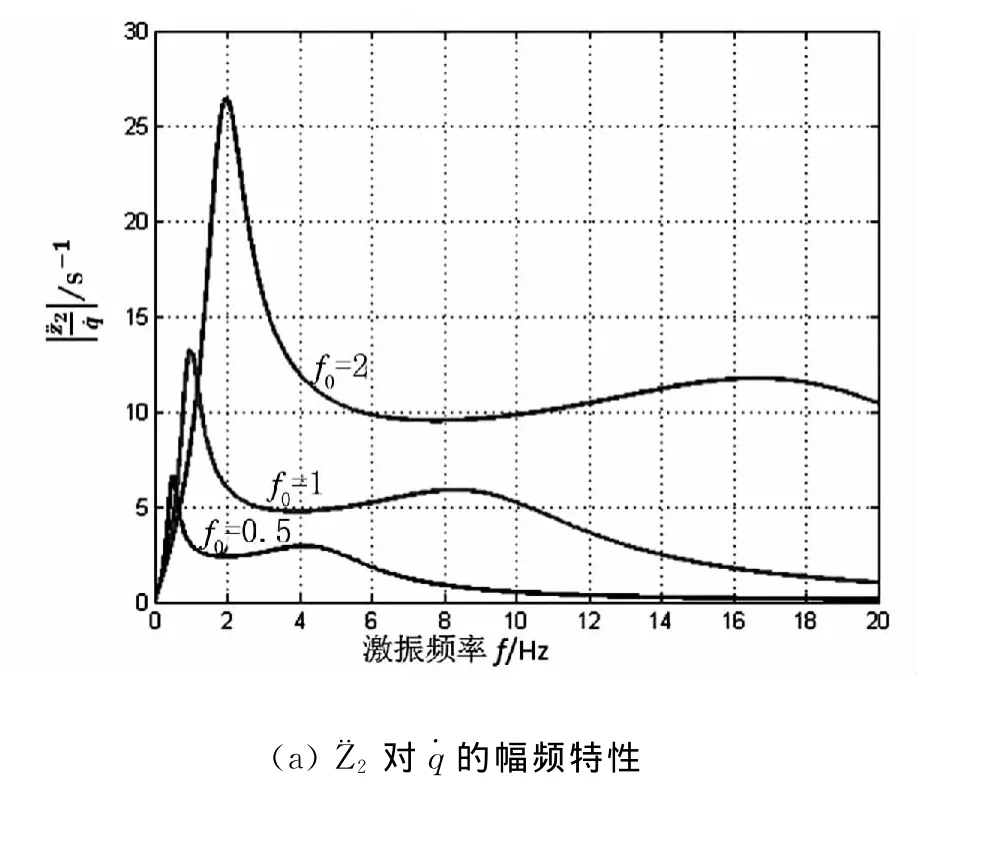
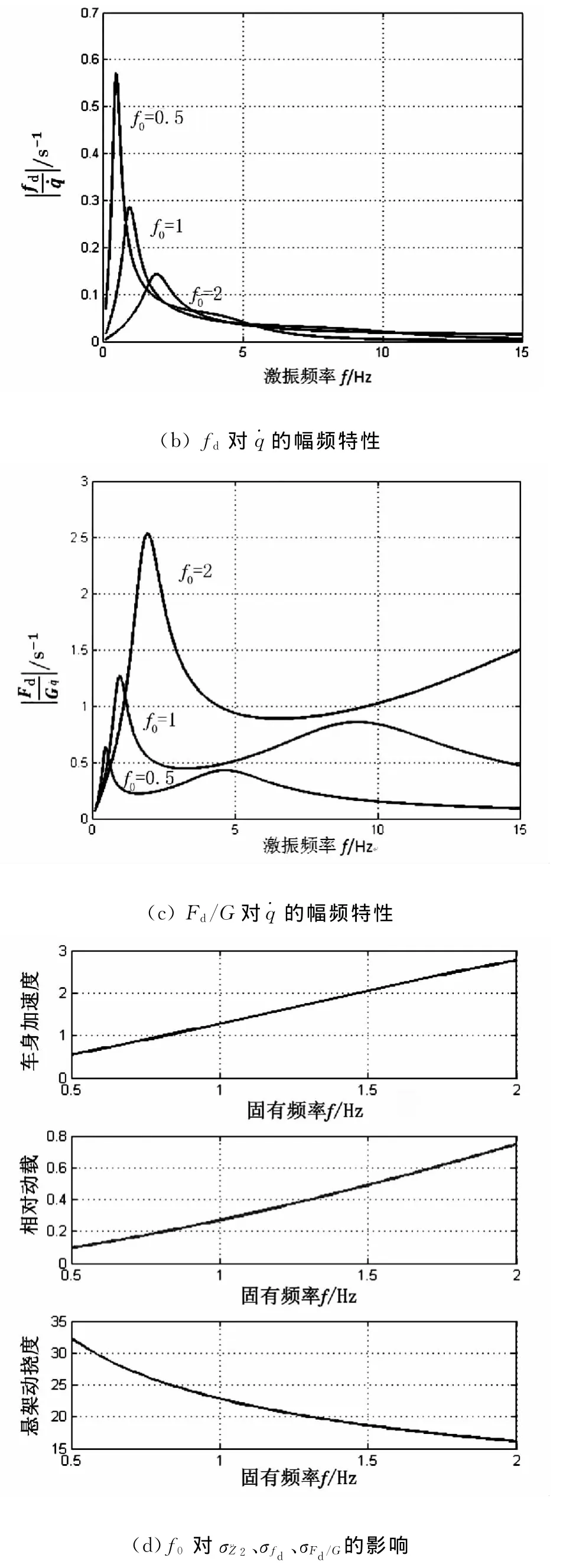
图2 f0 对振动响应量¨Z2、fd 和Fd／G的影响

从图2（d）中还可以看到，车身加速度和相对动载随着固有频率的增大而增大；悬架动挠度随着固有频率的增大而减小.3条曲线均近似于直线，可知振动响应量与车身固有频率接近于线性关系.

3.2 车身阻尼比ζ的影响

图3（a）－3（c）为阻尼比ζ取0.125、0.25、0.5，其他参数保持不变时，振动响应量¨Z2、fd和Fd／G对˙q的幅频特性.

由图3（a）－3（c）可见，阻尼比ζ对｜fd／˙q｜只在车身共振区和车轮共振区起作用，而且当ζ为0.5时，已不再呈现突出的峰值.输入的频率如果在系统共振段，将发生共振，使振幅明显增大.当加大阻尼比时，阻尼力能消耗一部分振动叠加的能量，因而使振幅不至于太大，阻尼比越大，对能量的消耗越大，振幅也就越小.从图3可以看出，阻尼比对低频段的影响不大.在高频的幅频特性随着固有频率的增加而增加.因为车身固有频率越高，相应的悬架挠度越大，在一定载荷下刚度段，输入的频率过高，远远超过系统的固有频率，这样，系统对输入的激振频率甚至来不及反应，所以输出的振幅会很小.频率越高，这种现象越明显，输出的振幅会越小.这就相当于，在高频阶段阻尼比越大，汽车悬架的刚度就越大，因而减振效果越不好，减小阻尼比ζ对减振更为有利.

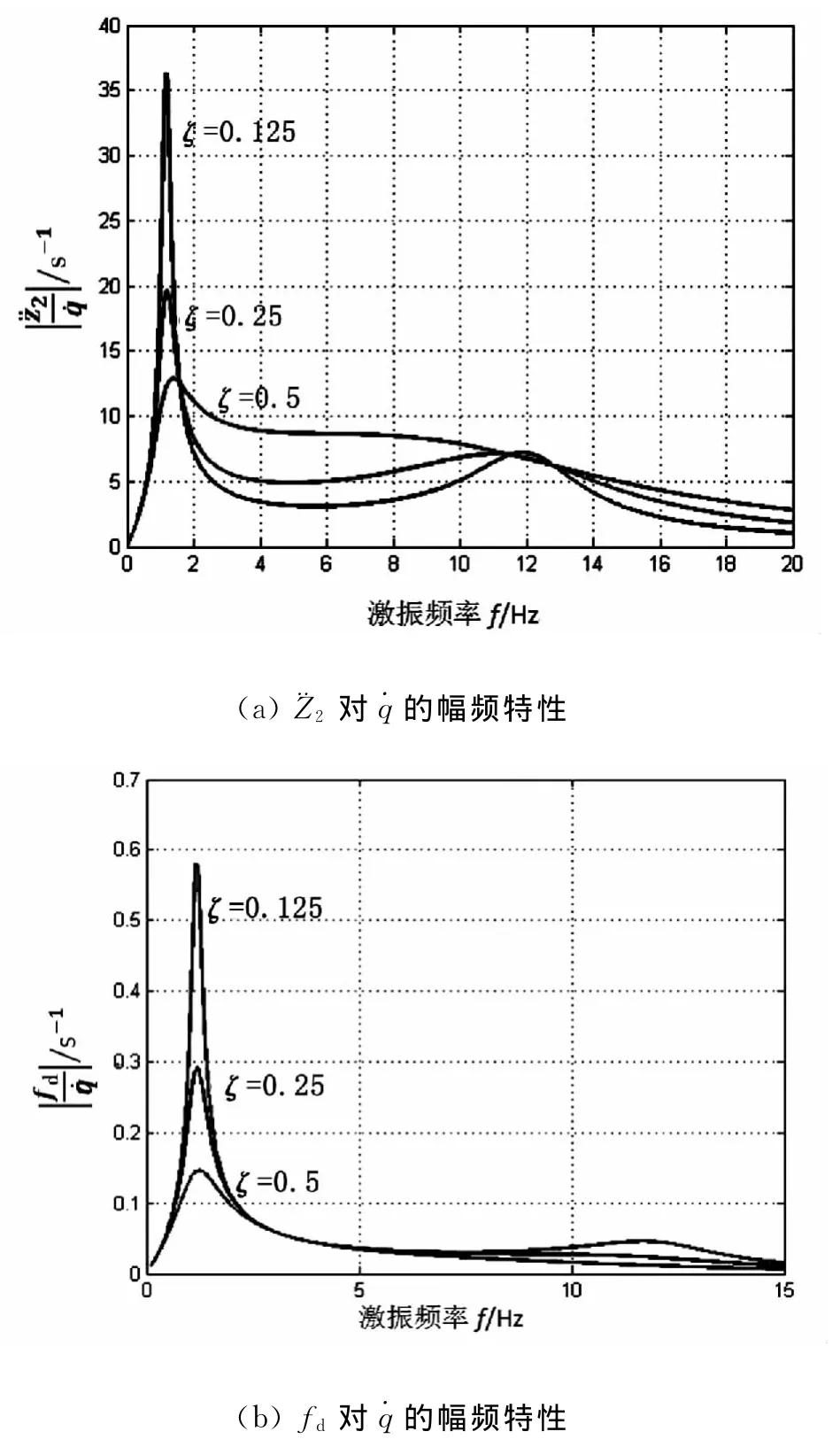
从图3（d）还可以看到，车身加速度随着阻尼比的增大而减小，直至在阻尼比处于0.3到0.4之间时达到最小值，然后逐渐开始上升.相对动载和悬架动挠度都随着阻尼比的增大而逐渐减小，在开始时随阻尼比变化显著，而后变化趋于平缓.

4 悬架的优化方案

为了优选出悬架阻尼比和固有频率的最佳组合，利用Matlab程序将悬架的阻尼比和固有频率逐一进行排列组合，然后代入验算，从中求出可以满足约束条件的组合并优选出最佳组合.Matlab程序设计的流程图如图4所示.

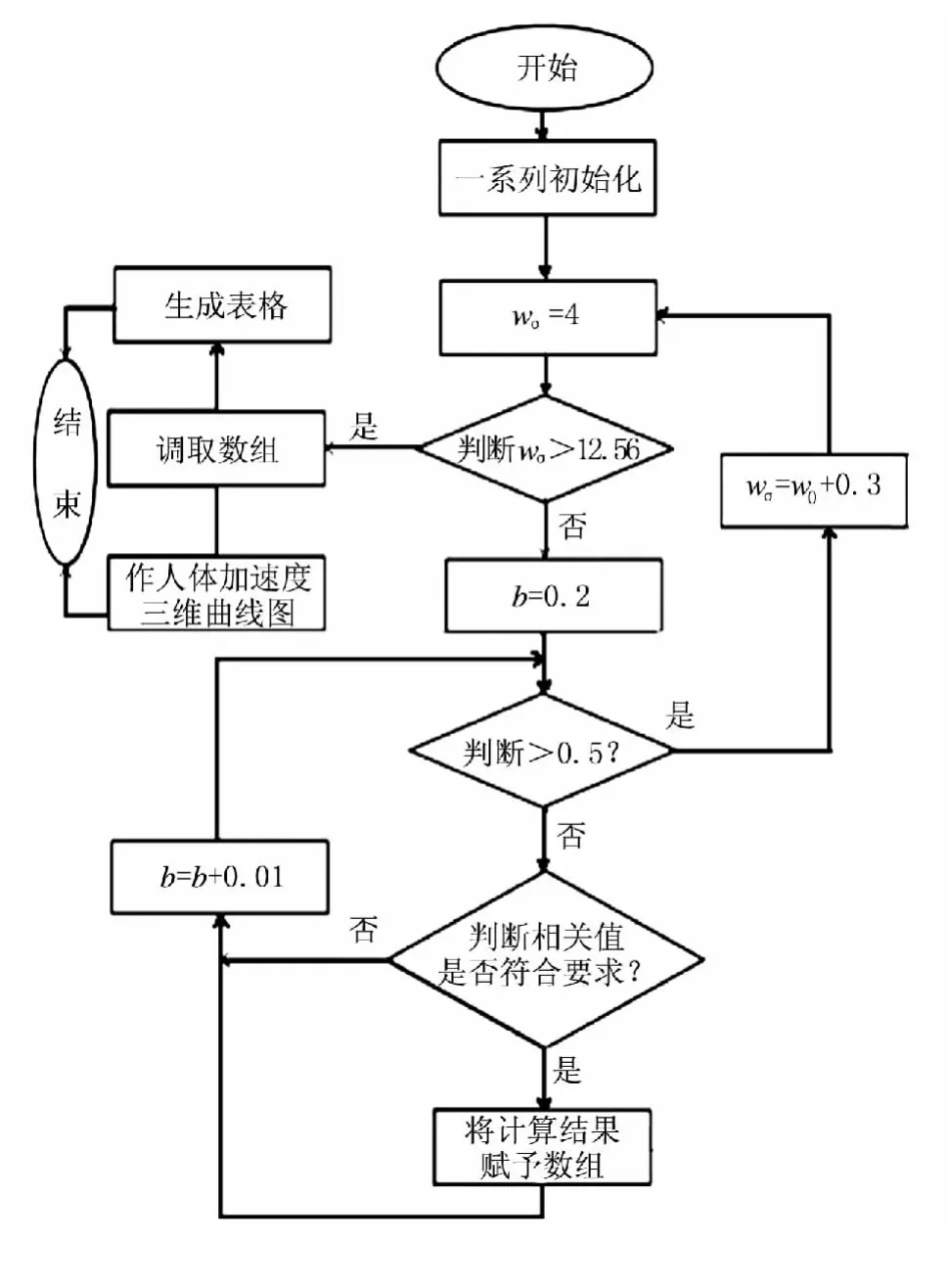
图4 悬架参数优化Matlab程序流程图

在C级路面上人体加速度随着阻尼比和固有频率的变化曲线如图5所示.从图中可以看到，在撞击悬架限位的概率和相对动载均满足相关要求的情况下，人体的加速度越小，乘员乘坐汽车的舒适性越高.考虑到汽车的其他性能，可以从中选择一组最优化的设计参数（如表1所示），使汽车既具有良好的行驶平顺性，又具有良好的制动性和操纵稳定性.

通过分析汽车原始设计参数及其运算结果可知，汽车在C级路面以50km／h的速度行驶时，人体加速度有效值为1.65m／s2，此时已经对乘员的舒适性造成一定的影响.相对动载为0.37时，λ＝2.69，通过查询正态分布，得P＝0.69%，车轮跳离地面的概率为0.345%，汽车的安全性相对比较低一点.但是，根据表悬架阻尼比为0.34.悬架参数优化前后人体加速度幅频特性曲线如图6所示，优化后的幅频特性要低于原值.在C级路面行驶时，人体加速度从1.65m／s2降到1.49m／s2，相对动载从0.37降到0.33，悬架动挠度虽然从20.45mm上升到22.22mm，但其撞击限位的概率依然控制在规定范围内.所以，优化后的悬架振动响应量人体加速度、动挠度和相对动载都能控制在一个合理的范围内，人体的舒适性进一步得到提高，汽车具有良好的行驶平顺性.中数据及前面分析可以得知，汽车悬架动挠度相对较小，也即是说在坏路运行时，撞击悬架的概率要稍微低一点.

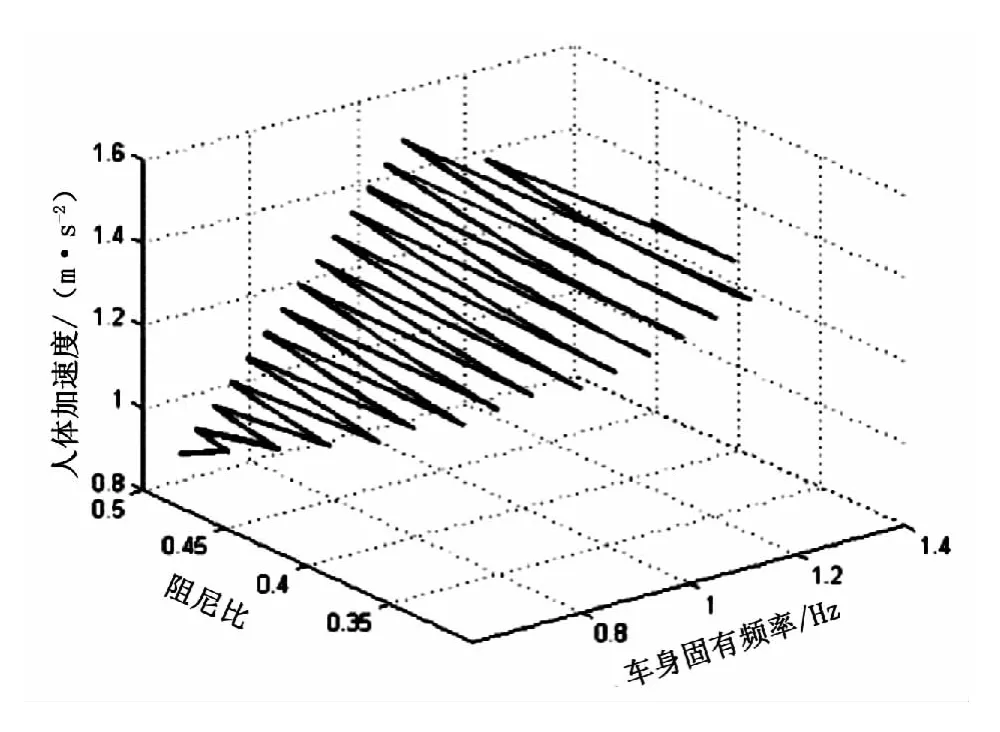
图5 C级路面人体加速度随着阻尼比和固有频率的变化曲线

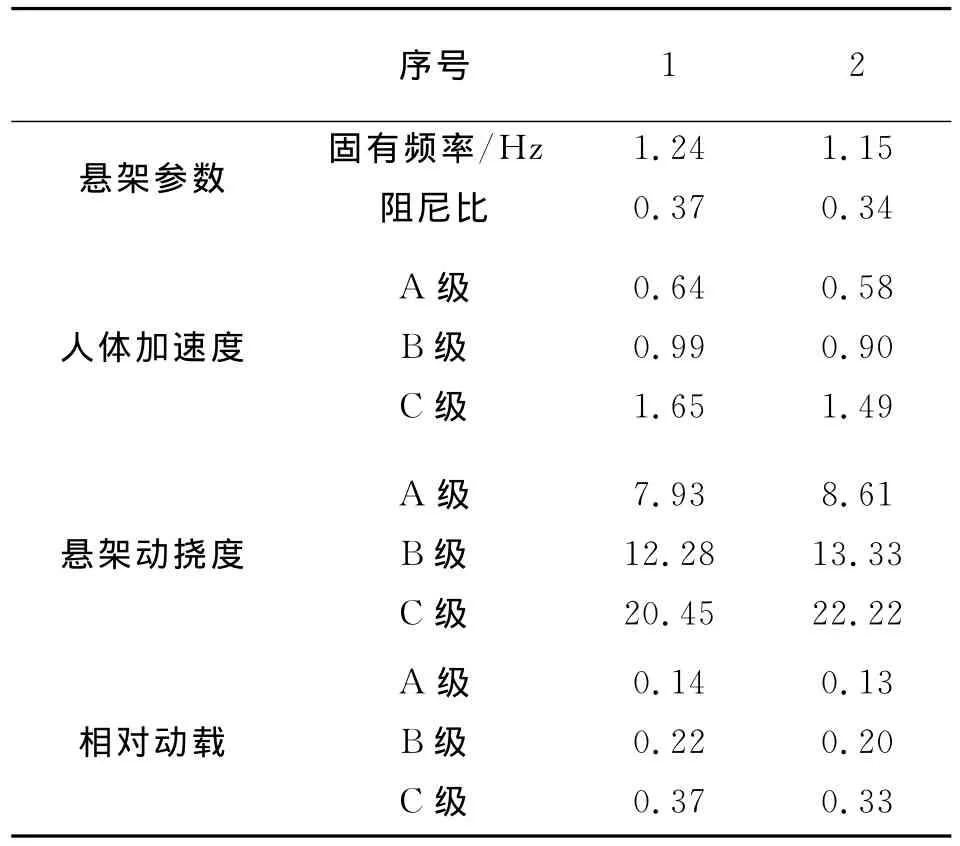
表1 通过Matlab程序运行优选出来的悬架参数

如表1中第2列数据，车身固有频率选择为1.15Hz，

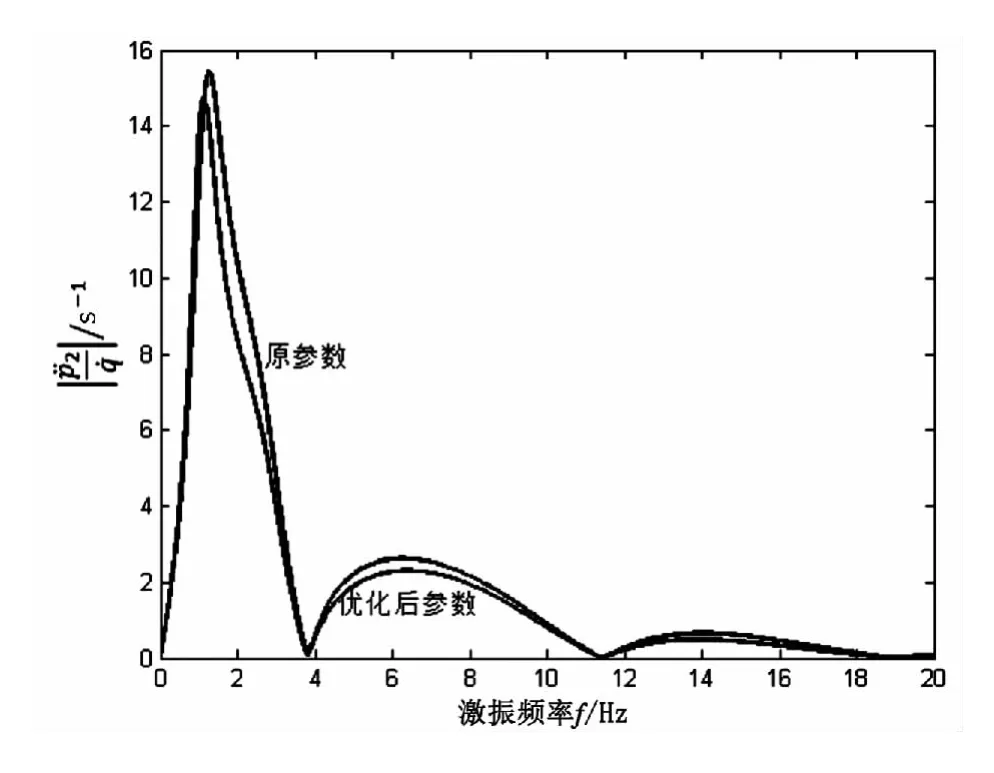
图6 悬架参数优化前后人体加速度幅频特性曲线

5 结 语

作为大众款的城市SUV，消费者更青睐的是其大空间以及较高的性价比，其越野性能在实际驾驶中很少得到应用.而且我国公路建设近年来不断取得进步，城市中的路况已经较为理想.所以，对于该型汽车来说，过多的追求越野性甚至以牺牲舒适性为代价是完全没有必要的.因此，在以不牺牲汽车安全性和操纵稳定性的前提下，可以适当降低悬架弹簧的刚度以提高汽车的乘坐舒适性.

［1］刘进伟，吴志新，徐达.基于 ADAMSCAR的某轿车悬架优化设计 ［J］.轻型汽车技术，2006，31（8）：4－7，14.

［2］汪随风，刘竞一，邓日青.基于ADAMS的双横臂独立悬架的仿真分析及优化设计 ［J］.湖北汽车工业学院学报，2007，21（2）：14－15.

［3］万里翔，许明恒.汽车行驶平顺性评价方法的研究 ［J］.西南交通大学学报，2001，36（1）：71－75.

［4］余志生.汽车理论［M］.北京：机械工业出版社，2009：120－154.