机织物热阻的理论模型研究

刘让同，李 亮，张 忠，郑贤宏

（中原工学院 河南省功能性纺织材料重点实验室，郑州450007）

服装作为人体的第二皮肤，人们希望它在寒冷的冬天具有保暖性，在炎热的夏天具有凉爽功能，这都与服装面料的导热性有关.热阻是表征材料导热性的重要指标，它与材料的种类、结构、组成等因素有关.国内外研究者从不同角度对服装面料的热阻展开研究，Famworth B在研究服装保暖性过程中阐述了其中的热流机制［1］，姚穆、刘让同等通过对毛型织物［2—3］、毛毡［4］的导热性研究，提出了毛型织物和无规纤维集合体的热阻模型，认为织物热阻是原料、厚度、容重三者的多元函数，并在此基础上提出了织物接触热阻的基本概念［5］.由于织物热阻的影响因素较多，有时还存在着多种因素的组合作用，这就使得分析时存在很多不确定因素，织物结构对织物热阻的影响可能更大.鉴于此，有必要对织物热阻的理论进行进一步研究.

1 织物热传导的宏观、微观机理

1.1 织物热传导的宏观机理

织物为纤维和空气的混合物，其热传递方式包括传导、对流、辐射和水汽传输发生的潜热传递.对于紧密织物，由于纱线中纤维间和纱线间缝隙孔洞较小，对流和辐射对热传递的贡献较小，热流在织物中的传递主要以热传导方式进行.

垂直流过织物的热流在织物内会形成等温面，等温面的走势趋于平行织物平面，实际上是一个曲折的曲面，织物内的热流方向并不总是沿着织物平面的法向，也不总是与等温面垂直，更多是沿着纤维轴向传递，并在适当的地方转移到另一根纤维上，接力进行.

在织物内部，存在着纤维—纤维界面与纤维—空气界面.在纤维—空气界面上，热流通过时会产生附加热阻.这就是接触热阻.纤维—纤维界面存在这样的附加热阻，在织物的两侧也存在这些接触热阻，热流进入和流出织物时都会受到接触热阻的阻碍.织物的总热阻值是接触热阻和织物本体热阻之和，如式（1）所示.

式中：Rt为纺织品的总热阻；R1为热流进入纺织品的接触热阻；R2为织物的本体热阻；R3为热流流出时织物的接触热阻.

1.2 织物热传导的微观机理

热流在材料中的传递本质上都是由微观粒子实现的，气体通过分子碰撞实现导热，金属通过自由电子导热，绝大多数无机非金属和纤维高聚物材料是通过晶格的振动导热，即声子导热［6］，在透明或者半透明的固体电解质中还存在着光子导热.

由于纤维是由线型大分子长链构成的，并且大部分沿着纤维轴向排列，纤维的取向结构使得纤维各种性能如湿膨胀、电学、光学、声学、热学等性能呈现各向异性.正是因为纤维的取向结构，所以声子沿着大分子排列的方向即纤维轴向传递时阻力较小，沿纤维径向传导阻力较大，因此纤维材料的热传导存在明显的各向异性.川端季雄对羊毛等多种纤维进行了测试，发现横向热阻与轴向热阻的比值为2.91～41.67［7］，纤维的横向热阻远大于纤维的轴向热阻，热流在织物中的传递势必沿着阻力最小的路径传递.因此，热流在纤维中主要沿轴向传递，在织物中主要沿纱线轴向传递.

2 不同组织机织物的热阻模型

热流在机织物中的传递是通过其中的传热通道来实现的，但对于不同的织物组织，其传热通道会有区别，传热通道数和每个通道的长度都不同.下面将以平纹、斜纹和5枚2飞纬面缎织物为对象研究机织物的热阻模型.

2.1 平纹机织物

对于平纹织物，其经、纬向截面图如图1所示.设机织物的经、纬纱的中心距和直径分别为bj、bw和dj、dw，一个组织单元中纱线的交织长度分别为lj、lw，其传热通道包括8条纤维通道、4条空气通道.

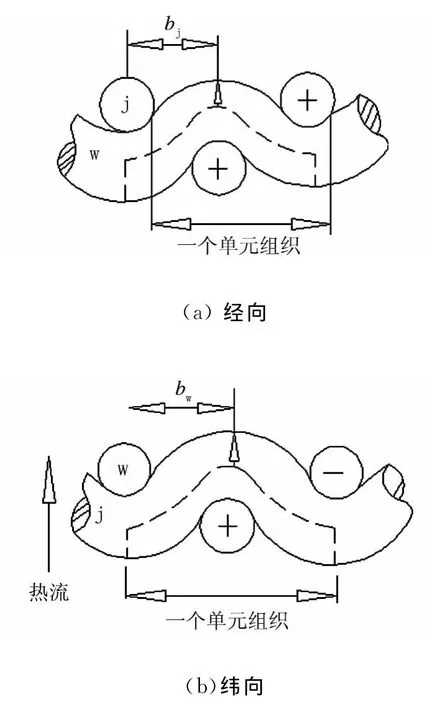
图1 平纹织物经向、纬向截面图

（1）空气通道共有4条，其中每条通道的长度为dj＋dw，传热面积为（bj－dj）（bw－dw）；

（2）沿纤维轴向传递的通道共有4条，其中由dj／2＋lj＋dj／2路径构成的通道有2条，每条通道的长度为dj／2＋lj＋dj／2，传热面积为经纱的截面积；由dw／2＋lw＋dw／2路径构成的通道也有2条，每条通道的长度为dw／2＋lw＋dw／2，传热面积为纬纱的截面积.

（3）沿纤维径向传导的通道共有4条，其中由dj＋dw路径构成的通道有2条，每条通道的长度为dj＋dw，传热面积为经、纬纱直径的乘积；由dw＋dj路径构成的通道也有2条，每条通道的长度为dw＋dj，传热面积为经、纬纱直径的乘积.

织物热阻就是这些通道热阻的并联，织物热阻表达如式（2）所示.

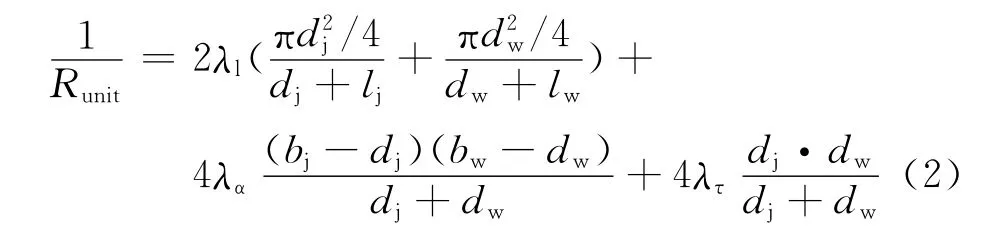
式中：Runit为一个组织单元的总热阻；λl为纤维轴向的导热系数；λα为空气的导热系数；λτ为纤维横向的导热系数.

2.2 1／2斜纹织物

对于斜纹织物，设织物的经、纬纱的中心距和直径分别为bj、bw和dj、dw，一个组织单元中交织长度分别为lj、lw.

（1）空气通道共有9条，其中每条通道的长度为dj＋dw，传热面积为（bj－dj）（bw－dw）.

（2）沿纤维轴向传导的通道共有6条，其中由dj／2＋lj＋dj／2路径构成的通道有3条，每条通道的长度为dj／2＋lj＋dj／2，传热面积为经纱的截面积；由dw／2＋lw＋dw／2路径构成的通道也是3条，每条通道的长度为dw／2＋lw＋dw／2，传热面积为纬纱的截面积.

（3）沿纱线径向传导的通道共有9条，其中由dj＋dw路径构成的通道有6条，每条通道的长度为dj＋dw，传热面积为经、纬纱直径的乘积；由dw＋dj路径构成的通道有3条，每条通道的长度为dw＋dj，传热面积为经、纬纱直径的乘积.

所以，斜纹织物一个组织单元的热阻如式（3）所示.

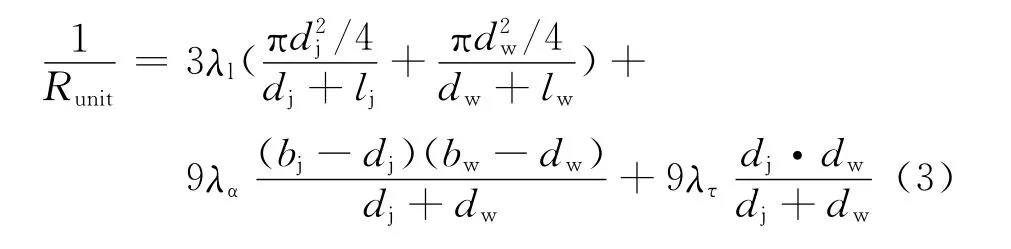
2.3 5枚2飞纬面缎织物

对于5枚2飞纬面缎织物，设织物的经、纬纱的中心距和直径分别为bj、bw和dj、dw，一个组织单元中交织长度分别为lj、lw.

（1）空气通道共有25条，其中每条通道的长度为dj＋dw，传热面积为（bj－dj）（bw－dw）.

（2）沿纤维轴向传导的通道共有10条，其中由dj／2＋lj＋dj／2路径构成的通道有5条，每条通道的长度为dj／2＋lj＋dj／2，传热面积为经纱的截面积；由dw／2＋lw＋dw／2路径构成的通道也有5条，每条通道的长度为dw／2＋lw＋dw／2，传热面积为纬纱的截面积.

（3）沿纱线径向传导的通道共有25条，其中由dj＋dw路径构成的通道有20条，每条通道的长度为dj＋dw，传热面积为经、纬纱直径的乘积；由dw＋dj路径构成的通道有5条，每条通道的长度为dw＋dj，传热面积为经、纬纱直径的乘积.

所以，5枚2飞纬面缎一个组织单元的热阻表达式如式（4）所示.

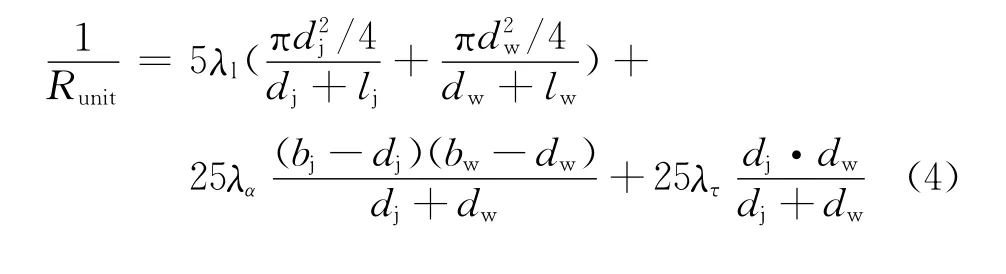
3 分析与讨论

3.1 织物热阻的一般模型

由上述平纹、斜纹、缎纹织物热阻的实例分析可知，织物热阻的影响因素主要有纤维材料的导热系数、纱线直径、织物组织、织物经纬密和容重等.纤维材料的导热系数越大，织物的热阻越小；纱线直径直接影响织物热阻；不同经纬密的织物其纱线中心距影响织物热阻.

织物组织是影响织物热阻的重要因素.从式（2）、式（3）和式（4）可以看出，平纹、斜纹、缎纹织物的热阻从组成上看是相似的，区别就在于通道个数，而通道个数又与织物单元组织循环纱线数有关.因此，对于不同织物的热阻，可以用通用模型式（5）进行描述.

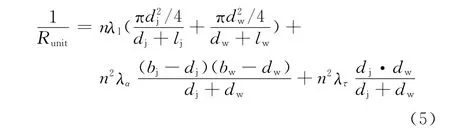
式中：n为织物一个组织单元的循环纱线数.

不同的织物组织其交织长度不同，导致热流在织物中所走的路径不同，热流通道越长，其热阻越大.由上述3种组织的一个组织单元的热阻表达式可知，缎纹织物一个组织单元通道数目为60条，斜纹织物热流通道数目为24条，平纹织物共有12条通道，各组织的热阻为各条通道的并联.因为热阻越并越小并且比其中最小的热阻还小，所以从织物本体热阻考虑，在其他条件一定的条件下，平纹织物热阻大于斜纹，斜纹织物热阻大于缎纹；再从接触热阻考虑，平纹织物交织次数多，纱线的屈曲程度大，接触热阻大.两点综合考虑，平纹织物热阻最大，斜纹大于缎纹.

3.2 热阻与织物厚度的关系

织物的厚度与纱线直径、经纬密的配置、织物组织等因素有关.但对于具体织物来说，纱线的直径和织物的经纬密是一定的，织物的厚度增加就意味着组织单元中纱线的交织长度lj、lw的增加.在式（5）中，等式右边的第一项是减小的，后两项保持不变，也就是说，织物厚度增加会使织物热阻增加.

为了进一步说明，假设织物的经、纬纱直径相同，经、纬纱的交织长度相同，那么式（5）就变成了式（6）.

对式（6）两边的厚度t同时求偏导，可以得到

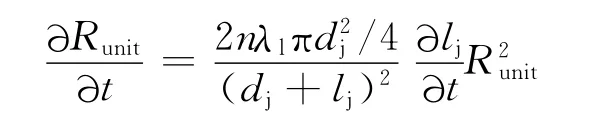
3.3 热阻与织物容重的关系

织物容重也是影响织物热阻的重要因素.经、纬纱交织长度以及经、纬纱中心距均为容重的函数.对式（6）两边的容重δ同时求偏导，可以得到

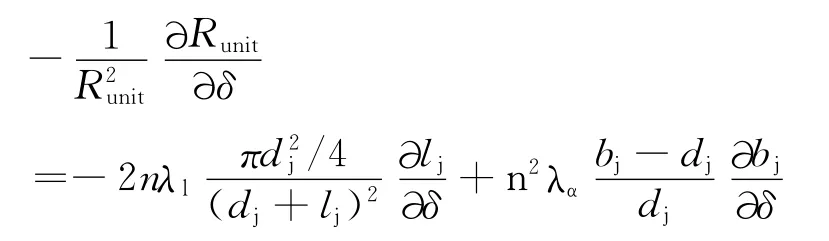
当容重增大时，经、纬纱交织长度lj、lw减小，经、纬纱中心距bj、bw减小，即同时纱线之间会互相挤紧，（bj－dj）会越来越趋近于零，空气通道消失.这时，，可见，即织物热阻随容重的增加而减小.

织物热阻的最终影响因素是织物中的空气含量.织物容重（体积密度）会直接影响织物中空气含量.

影响织物热阻的因素有许多，有时还存在着交互作用，共同影响织物热阻，因此织物热阻分析具有不确定性.已有研究结果显示，对于紧密织物而言，织物热阻实际上是原料、厚度、容重的多元函数.

4 结 语

（1）分析了织物热传导的宏观、微观机理，认为热流在织物中的传递具有各向异性，热流在纤维中主要沿轴向传递，在织物中主要沿纱线轴向传递.

（2）织物的热阻是与织物的传热通道数目、通道长度密切相关的.通过对平纹、斜纹、缎纹织物热阻的实例分析，建立了织物热阻的理论模型.

（3）在织物热阻理论模型的基础上，分析了织物组织、厚度和容重对织物热阻的影响规律，丰富了织物热传递理论.

［1］Famworth B.Mechanism of Heat Flow Through Clothing Insulation［J］.Textile Research Journal，1983，53（12）：717－725.

［2］姚穆，刘让同.纺织品热阻的研究［J］.西北纺织工学院学报，1991，5（2，3）：77－83.

［3］姚穆，刘让同.毛型织物热阻的研究［J］.纺织学报，1991（8）：4－7.

［4］刘让同.无规纤维集合体热传递性能的研究［J］.纺织学报，1995（10）：8－11.

［5］刘让同.纺织品接触热阻产生机理分析及实验研究［J］，纺织中心期刊（台湾），1995，5（3）：225－229.

［6］黄昆.固体物理学［M］.北京：北京大学出版社，2009.

［7］川端季雄.单纤维的热传导率的异分性的测试［J］.纤维机械学会志，1986，3（12）：317－319.