基于三点分段的一类三角样条曲线的扩展

潘亚丽

淮北师范大学数学科学学院，安徽淮北，235000

近年来,三角样条和三角多项式在理论和实际应用中受到广泛的关注，文献[1]在三角多项式空间Cm=Span{1,cost,cos2t,…,cosmt}给出了一个三角多项式基。文献[2]将多项式与三角多项式有机结合起来,得出具有参数α的曲线,作者称为C-曲线。文献[3]提出在空间W=Span{1,sint,cost,cos2t}构造具有与二次B样条相类似的三角基函数,且保持曲率连续；文献[4]中提出针对与二次代数样条相类的一类曲线的扩展，扩展后的曲线可通过参数来进行曲线的局部调整，且四次调配函数可达G2连续，以后随着调配函数次数的升高，连续性也逐渐提高。相关的工作参看文献[6]～[8]。本文提出基于三点分段的一类三角B样条曲线的扩展，构造出带局部参数λi的二次和三次调配函数，且当λi=0时退化为文[5]中的一次和二次基函数。本文所采用的方法为连续性要求较高的曲线设计提供了一种有效的方法。

1 曲线的生成

定义1对t∈[0,π/2]，λi∈R，称关于t的三角多项式：

(1)

为带参数λi的二次调配函数，其中-1≤λi≤1。

定义2对t∈[0,π/2],λi∈R,称关于t的三角多项式：

(2)

为带参数λi的三次调配函数，其中-2≤λi≤1。

定理1对调配函数(1)、(2)式有如下结论成立：

直接由(1)和(2)的调配函数以及三角函数的性质可得定理的结论。同时，当λi=0时，本文中的(1)和(2)式就变成文[5]中的一次和二次的情况，所以它们可以看成文献[5]中的调配函数的扩展。

定义3设Pi(i=0,1,…,n)为R2或R3中的一组控制点(n≥2)，对每三个顺序控制点Pi-1,Pi,Pi+1构造一参数曲线段：

(3)

将所有曲线段Ri,m(λi,t)(i=0,1,…,n)组合在一起，得到曲线：

(4)

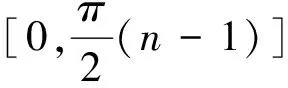
2 曲线的性质

定理2(a)λi∈(-1,1)，曲线Ri,2(λi,t)(i=1,2,…,n-1)是G1连续的；

(b)当所有的λi相同时，曲线是G1连续的；

(c)当λi=1时，曲线达到G2连续。

证明：由(1)和(4)式直接计算可得：

当λi∈(-1,1)时

(5)

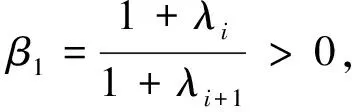
(6)

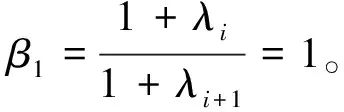
(7)

从而结论(b)与(c)成立。

定理3(a)λi∈(-2,1)，曲线Ri,3(λi,t)(i=1,2,…,n-1)达到G3连续；

(b)λi=1,曲线Ri,3(λi,t)(i=1,2,…,n-1)达到G4连续。

证明：由(2)和(3)式直接计算可得：

当λi∈(-2,1)(i=1,2,…,n-1)时

(i=1,2,…,n-3)

(8)

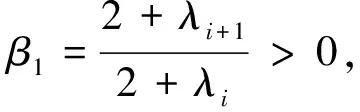
(9)

成立，所以曲线是G2连续的。令：

(10)

则等式：

(11)

成立，所以曲线是G3连续的。

当λi=1(i=1,2,…,n-2)时，可计算曲线的四阶导数值：

由上述计算可知，当λi=1(i=1,2,…,n-1)时，β1=1,β2=-4,β3=24，若令β4=-248，则等式:

(12)

恒成立，所以当λi=1(I=1,2,…,n)时是G4连续的，证毕。

3 数值例子

本节给出两个数值例子，分别使用本文的二次和三次调配函数构造相应的曲线。这两个曲线的形状都可以进行局部的调整。

例1假设有控制顶点V0=(0,0),V1=(10,20),V2=(30,15),V3=(40,30),V4=(60,15),使用二次调配函数所构造的曲线，如图1所示，其中，λi=-0.5,0,0.5(i=1,2,3)，该曲线是G1连续的。

例2假设有控制顶点V0=(0,0),V1=(10,20),V2=(30,15),V3=(40,30),V4=(60,15),使用三次调配函数所构造的曲线，如图2所示，其中，λi=-2,0,0.5(i=1,2,3)，该曲线G3是连续的。

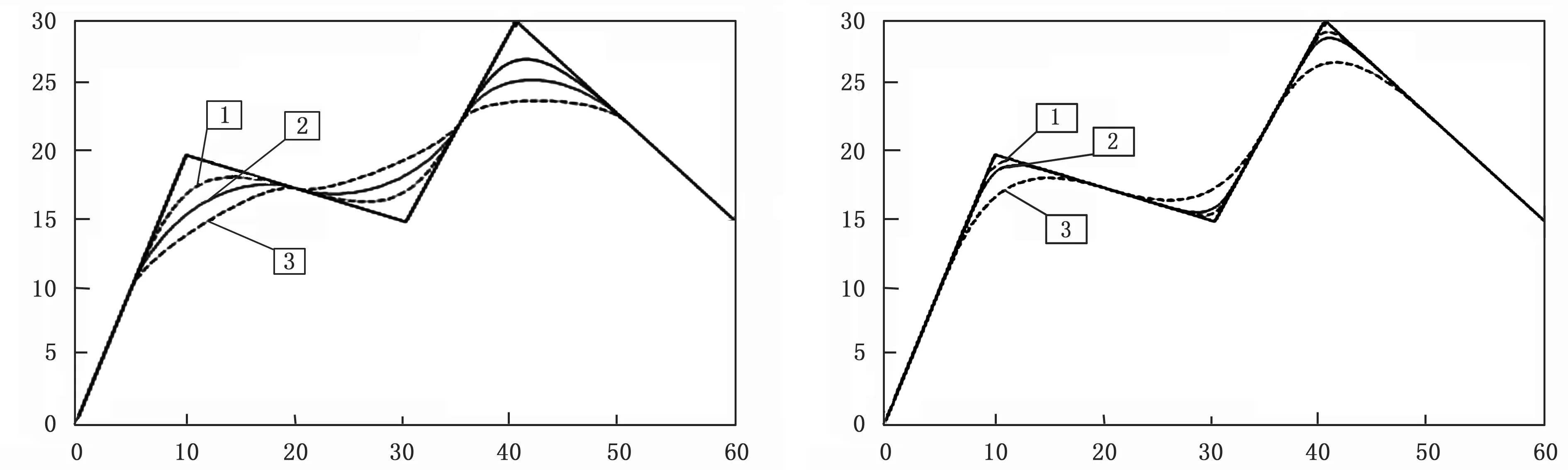
图1 二次调配函数 图2 三次调配函数

参考文献：

[1]J M Pena.Shape Preserving Representations For Trigonometric Polyomial Curves[J].Computer Aided Geometric Design,1997,14:5-11

[2]Jiwen Zhang.C-curves:An Extension of Cubic Curves[J].Computer Aided Geometric Design,1996,13:199-217

[3]吴小勤,唐运梅.曲率连续的三角B样条曲线与曲面[J].计算机应用与软件,2005,22(1):118-120

[4]刘长明,檀结庆.二次均匀B样条曲线的扩展[J].合肥工业大学学报：自然科学版,2004,27(5)：459-462

[5]吴小勤.基于三点分段的三角多项式样条曲线[J].工程图学学报,2005(2):101-105

[6]尹池江,檀结庆.带多形状参数的三角多项式均匀B样条曲线曲面[J].计算机辅助设计与图形学学报,2011,23(7):l131-1138

[7]夏成林,邬弘毅,郑兴国，等.带多个形状参数的三次均匀B样条曲线的扩展[J].工程图学学报,2011,31(2):73-79

[8]严兰兰．带形状参数的三角曲线曲面[J].东华理工大学学报：自然科学版,2012，35(2)：197-200