Weibull分布型元件串联系统的可靠性广义置信区间
卢勤勤, 李新民, 张 霞
(1.山东理工大学 理学院, 山东 淄博 255091; 2. 青岛大学 数学科学学院, 山东 青岛 266071; 3. 山东省淄博市公路管理局, 山东 淄博 255000)
Weibull分布广泛应用于可靠性工程,是可靠性工程中重要的分布,其概率密度为
(1)
其中λ>0为尺度参数,k>0为形状参数.其在t时刻的可靠度函数
对于单个Weibull分布型元件的定时结尾数据的可靠性函数的置信区间已得到较好解决[1],但对于有两个Weibull分布型元件组成的串联系统,却极少有文献对其系统可靠性的置信区间进行研究.本文将基于Weerahandi[2]的广义枢轴量和广义置信区间的概念,建立系统可靠性的广义置信区间.因此,本文中对广义枢轴量和广义置信区间的基本概念和理论进行介绍,然后基于服从Weibull分布的两个元件的定时结尾数据构造了R(t)广义枢轴量以及其广义置信区间,并且在此基础上,又讨论了广义置信区间的频率性质.并从理论上证明了由广义枢轴量所确定的可靠性的广义置信区间就是频率意义下的实际置信水平.
1 可靠性函数的广义置信区间
1.1 串联系统的可靠性

R(t)=R1(t)R2(t)=
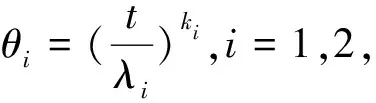
1.2 广义置信区间
由于讨厌参数的存在,很难利用传统的建立置信区间的方法得到精确的置信区间. Weerahandi[2]给出了广义区间估计的概念.设X为观测向量,其密度函数为f(x,ξ),ξ=(θ,η)为未知参数,其中θ∈Θ为兴趣参数,η为讨厌参数.令T=t(X;x,ξ)是X,x和ξ的函数,如果T满足以下两条性质:
(i)∀x,T的概率分布Px与未知参数无关;
(ii)若X=x,t(x;x,ξ)不依赖于讨厌参数η,则称T为广义枢轴量.
于是,对给定的置信水平γ,任意给定x,可以定义θ的广义置信区间.
1.3 基本构造方法

其中,函数f(t)=ete-et,-∞ (2) (3) 则,由Hannig等[6]知,μi和σi的Fiducial模型为 (4) 于是θ1+θ2的Fiducial模型为 (5) (6) 由于求解可靠性R(t)的广义枢轴量的精确分布比较困难,下面给出了计算广义置信区间的模拟计算方法,步骤如下: 1)对于给定样本数据Y1,Y2,…,Yn1和Y1,Y2,…,Yn2我们通过换元的方法,令Z=lnY得到服从极值分布的定时截尾寿命数据Z1,Z2,…,Zn1,Zn1+1,Zn1+2,…,Zn1+n2. 4)由以上数据及公式(5),计算Tθ1+θ2的观测值为T(θ1+θ2)i. 5)将T(θ1+θ2)i由大到小排序,的到其顺序统计量T(θ1+θ2)(1) (exp(-T(θ1+θ2)(U)),exp(-T(θ1+θ2)(L))). 广义置信区间的覆盖率并不一定等于我们要求的置信水平,下面将通过数值模拟的方法研究所得可靠性函数R(t)的广义置信区间的频率性质. 对于由两个独立的Weibull元件组成的串联系统,两Weibull分布的样本容量分别为n1=n2=10,并且当形状参数取值为k1=k2=1时,尺度参数分别为λ1=λ2=2,10;当k1=k2=2时,尺度参数分别为λ1=λ2=2,置信水平为1-α=0.95,模拟次数为M=1 000次.在计算R(t)的广义置信区间时,对于每一个样本数据,标准极值分布的样本容量均为N=1 000次.计算结果见表1. 表1 可靠性函数的广义置信区间的覆盖率 从表1中可以看出,可靠性函数的广义置信区间覆盖率比较稳定,且当尺度参数较大时比较接近真实的置信水平. 本文对由两个独立的两参数Weibull分布分别组成的串联系统,利用广义枢轴量以及广义置信区间的概念,将原样本数据换元后得到服从极值分布的样本数据,构造其所需要的Fiducial模型,建立了它的可靠性函数的广义置信区间,并给出了计算R(t)的广义置信区间的算法.模拟结果表明广义置信区间的覆盖率比较令人满意. [1]赵桂梅,崔玉杰.Weibull分布兴趣参数的广义置信区间[J].工程数学学报, 2010,27(6):567-570. [2] Weerahandi S. Generalized confidence intervals[J]. JAmer Statist Assoc, 1993,88: 899-905. [3] 董岩,徐兴忠.双参数指数分布型元件串联系统的可靠性的广义置信区间[J].应用数学学报, 2011,34(6):1 023-1 031 [4] 徐兴忠,李国英.枢轴分布族中的Fiducial推断[J].中国科学:A辑,2006,36(3):340-360. [5] Hannig J, Iyer H, Patterson P.Fiducial generalized confidence interval[J]. J Amer Statist Assoc, 2006,101: 254-269.

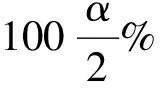


2 模拟计算

3结束语

