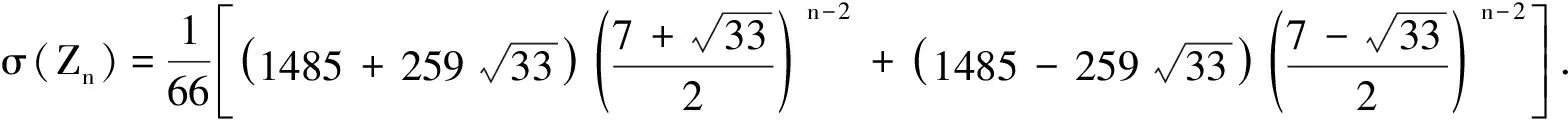四角链的Merrifield-Simmons指标
田文文, 田双亮
(西北民族大学 数学与计算机科学学院, 甘肃 兰州 730030)
1 预备知识
设G=(V,E)是一个简单图,它的点集和边集分别为V(G)和E(G).令e和x分别为图G的一条边和一个顶点,我们用G-e表示图G删去边e得到的图,用G-x表示图G删去顶点x(及关联的边)得到的图.若A⊆V(G),对任意的两个顶点u,v∈A,都有uv∉E(G),则称A为图G的一个独立集,其中空集为任何图的一个独立集.本文中Fn表示Fibonacci数,即满足Fn=Fn-1+Fn-2,n≥2,且F0=0,F1=1.文中未加说明的符号及术语参见文献[1].
Merrifield-Simmons指标是1989年由美国化学家Richard E.Merrifield和Howard E.Simmons在文献[2]中引入的化学拓扑指标.它表示图G中所有独立集的数目,记为σ(G).该指标与物质的沸点有着密切的联系,且有着较为广泛的应用,有关的应用及部分最新研究成果参见文献[2-4].文献[5]中对两类四角系统的匹配数与点独立集数进行了研究.文献[6]中研究了关于k-匹配和k-独立集的极值四角链.本文通过构造一类特殊的四角链,即由n个单位正方形序列且任意相邻两个正方形之间只有一条割边构成的连通图,研究该类四角链在两种不同构联接位下的Merrifield-Simmons指标,并给出具体表达式.
定义1设Q1,Q2,…,Qn为n个单位正方形序列,则称该序列为四角链,如果满足:
(i)对任意的1≤s (ii)每个正方形与割边的顶点都为3度顶点. 用Φn表示含有n个单位正方形构成的四角链的全体.设Gn∈Φn,一个四角链Gn(n≥2)可由Gn-1再联接一个单位正方形得到,如图1所示.每个链中的正方形有3个可联接位,但其中与接点距离相等的2个可联接位1和1′是同构的,所以只有两种非同构的联接方式Gn-1→[Gn-1]k=Gn,其中k=1,2分别称为1-位联接和2-位联接. 图1 两种连接方式 特别地,若四角链Gn中的每个单位正方形都以1-位联接的方式联接在前一个正方形上,则记为Zn;若四角链Gn中的每个单位正方形都以2-位联接的方式联接在前一个正方形上,则记为Ln,如图2所示. 图2 四角链Zn和Ln 在证明主要结论之前,我们先介绍以下几个引理: 引理1[4]设G是一个图,对∀uv∈E(G),u∈V(G) ,令NG[u]={u}Y{v|uv∈E(G)}, 则有σ(G)=σ(G-u)+σ(G-NG[u]). 引理3[4]设Pn为n阶的路,则σ(Pn)=Fn+2. 引理4[4]设Cn为n阶的圈,则σ(Cn)=Fn+1+Fn-1. 关于四角链在两种非同构联接位下的Merrifield-Simmons指标,我们可以得出以下的结论. 定理1对于任意的正整数n≥2,有 证明如图2所示,根据引理可得 (i)因为σ(Zn)=σ(Zn-un)+σ(Zn-NZn[un])=σ(P3)·σ(Zn-1)+σ(P1)·σ(Zn-1-vn-1)= F5·σ(Zn-1)+F3·σ(Zn-1-vn-1)=5σ(Zn-1)+2σ(Zn-1-vn-1)= σ(Zn-vn)=σ(Zn-vn-un)+σ(Zn-vn-NZn-vn[un])=σ(P2)·σ(Zn-1)+σ(P1)·σ(Zn-1-vn-1)=F4·σ(Zn-1)+F3·σ(Zn-1-vn-1)=3σ(Zn-1)+2σ(Zn-1-vn-1)= (ii)因为σ(Ln)=σ(Ln-un)+σ(Ln-NLn[un])=σ(P3)·σ(Ln-1)+σ(P1)·σ(Ln-1-vn-1)= F5·σ(Ln-1)+F3·σ(Ln-1-vn-1)=5σ(Ln-1)+2σ(Ln-1-vn-1)= σ(Ln-vn)=σ(Ln-vn-un)+σ(Ln-vn-NLn-vn[un])=σ(P1)·σ(P1)·σ(Ln-1)+σ(Ln-1-vn-1)= F3·F3·σ(Ln-1)+σ(Ln-1-vn-1)=4σ(Ln-1)+σ(Ln-1-vn-1)= 定理2对于任意的正整数n≥2,有 [1] Bondy J A,Murty U S R.Graph Theory with Applications[M].New York:The Macmillan Press,1976. [2] Hosoya H.Topological index[J].Bull Chem Soc Japan,1971,44:2 332-2 339. [3] Merrfield R E,Simmons H E.Topological Methods in Chemistry[M].New York:Wiley,1989. [4] Gutman I,Polansky O E.Mathematical Concepts in Organic Chemistry[M].Berlin:Springer,1986. [5] 张莲珠.两类四角系统的匹配数与点独立集数[J].数学研究.1999,32(3):310-315. [6] Zeng Y Q,Zhang F J.Extremal polyomino chains onk-matchings andk-independent sets[J].Journal of Mathematical Chemistry,2007,42(2):125-140.


2 主要结论及其证明



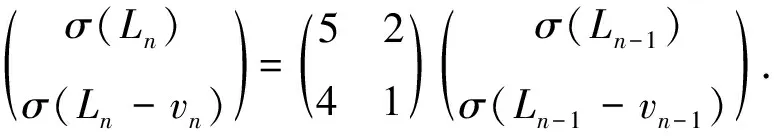



3 进一步的结果