基于贝叶斯推断模型的中国商业银行内部欺诈研究

高丽君，杨丰睿

(1.山东财经大学工商管理学院，山东济南 250014;2.中国石化山东石油分公司，山东 济南 250014)

一、引 言

自上世纪90年代以来，巴林银行倒闭、法国兴业银行事件及中行开平案等国内外操作风险事件对银行业产生致命的打击;巴塞尔新资本协议规定除信用风险和市场风险之外必须为操作风险分配资本金，对操作风险进行管理已成为银行业不可回避的话题。操作风险已成为对银行来说仅次于信用风险的一个重要风险。中国银监会按照巴塞尔协议Ⅱ、Ⅲ的要求，规定自2013年国内所有银行必须全部实施新资本协议。这意味着为操作风险分配资本金对中国商业银行来说已经不是“遥不可及”的事情。

目前学术界和业界正加大对操作风险的研究力度，但多数文献是针对操作风险的损失强度进行度量的，由于操作风险本身具有损失事件发生频率低，损失金额分布范围广以及具有一定的厚尾性的特点，且中国商业银行操作风险损失事件的有效记录历史时间不长，数据积累不多等原因，给操作风险的度量带来了一定的困难，进而影响操作风险资本金的有效配置，这也是目前商业银行操作风险管理面临的主要问题。按照巴塞尔银行监管委员会在新资本协议中对操作风险提出的两种分类方式，中国商业银行在内部欺诈事件类型方面损失严重，可以认为内部欺诈是中国商业银行操作风险管理的重点。

操作风险的度量模型很多，其中损失分布法是巴塞尔委员会推崇的一种计量法，损失分布法能准确地对操作风险进行估计［1］，是未来的主要发展趋势之一。损失分布法假设发生次数和严重程度是独立的，估计操作风险损失在一定时期内的概率分布及其参数，然后将频度分布和程度分布通过一定的方法(如蒙特卡罗模拟等方法或者事先假设具体的概率分布形式)集成起来得到一年的操作风险损失分布，从而计算操作风险的大小。对操作风险进行估算的主要目的之一，是为了确定为操作风险而分配的监管资本，因此需要计算出给定置信水平之下操作风险的分位数，在一定的置信水平下(如99.9%)，操作风险的在险价值(VaR)直接度量了最大可能损失。但由于操作风险损失事件的有效记录历史比较短，很难获得充分的数据，因此如何利用仅有的、稀缺的数据准确地度量操作风险成为一个很困难的问题。为了克服数据不足问题，本文考虑使用贝叶斯推断的方法度量操作风险。本文在对操作风险度量模型分析的基础上，应用贝叶斯推断来对中国商业银行操作风险内部欺诈进行度量，可以较好地解决目前操作风险损失事件数据不足的问题。

二、中国商业银行操作风险及内部欺诈现状分析

本文利用公共信息渠道收集了40多家银行1994年至2011年1539条中国商业银行的操作风险损失事件信息。每一事件都记录了以下方面的信息:事件发生、发现及结束的时间、地点，事件的责任主体，事件发生的业务类别和事件类别，损失大小、损失收回的金额及其收回的途径，是否与市场风险和信用风险相关，事件原因的描述等内容。表1给出中国商业银行操作风险损失的年度统计信息，中国商业银行操作损失频发，损失额均值为23740万元，损失数额巨大，给银行业务及其声誉带来极大负面影响。

表1 中国商业银行操作风险损失样本数据分析

表2 我国商业银行内部欺诈样本数据的统计描述

由表2可以看出，我国商业银行的操作风险就事件类型而言内部欺诈是一个非常重要的事件类型，无论损失强度还是损失发生的次数都非常惊人。我国商业银行操作损失事件主要来源于银行内部，特别是银行内部人员或内部人员与外部人员相互勾结所进行的主观的、故意的欺诈行为，据不完全同统计，发生的次数超过900次，损失频率及损失金额占比均超过60%。因此，内部欺诈事件类型是中国商业银行操作风险管理的重点，加强内部员工的道德素质教育和职业操守教育，提高内部控制水平，对操作风险管理水平的提高具有重要意义。

三、贝叶斯推断

采用传统方法度量的缺陷在于样本信息不可能完全准确，会对结果准确性产生较大影响。贝叶斯方法的是使用先验分布，度量过程中结合先验信息和样本信息，利用后验分布综合了先验信息，总体信息和样本信息，对较小样本也有较好的推断效果。

在先验分布中，经常有未确定的参数(超参数)，利用先验矩方法可得超参数的估计值。利用贝叶斯推断来度量操作风险时，先验分布的选取至关重要，常用的方法是选取共轭先验分布。共轭先验分布计算方便，且后验分布的一些参数可以得到很好的解释。但并非所有的分布均有共轭分布，因此，有时需单独对分布的参数进行分析。

1.操作风险损失频率先验分布

根据操作风险损失频率的特征，操作风险损失频数的分布常常设为Poisson和负二项分布［2］，因此，我们分析Poisson分布p(λ)λ均值的共轭先验分布和负二项分布的共轭先验分布。

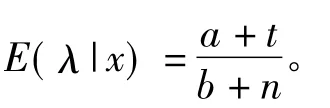
2.操作风险损失强度的先验分布

根据操作风险损失强度的尖峰厚尾特征，操作风险损失强度的分布常常设为极值分布或对数正态分布。

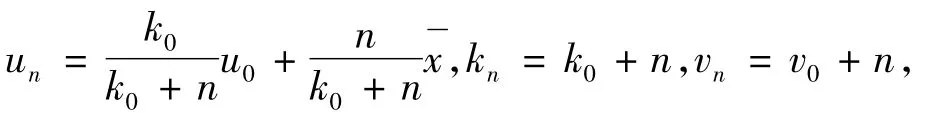
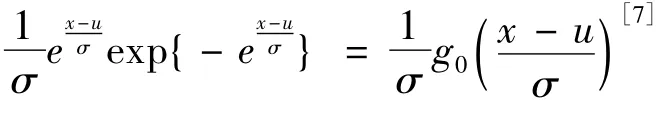
3.联合分布

根据损失分布法的思想，每一业务线和事件类型组成的子集i的总损失可以定义为一定时期t随机损失nt的和，即Lit=Xi1+Xi2+… +Xint，这里，Lit代表总操作风险损失，Xi1+Xi2+… +Xint代表个体损失强度，而nt代表损失频率。因此，对每一子集，对每一时间段，总损失可表示为Lt=st×nt，这里nt代表损失频率，而st代表某时间段的损失强度的均值。

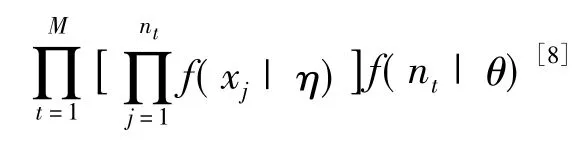
四、实证分析

1.先验超参数估计使用的数据

有关先验分布中超参数估计的数据，本文援引中科院政策所商业银行操作损失数据库的的操作风险损失数据，得到1993年到2006年每年损失频数和损失强度均值的数据(见图1)。

2.损失频率分布估计

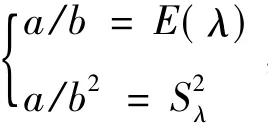
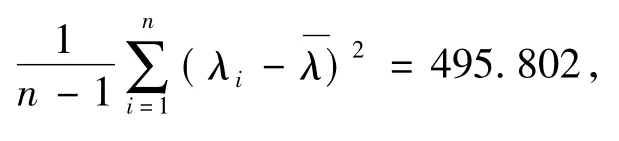
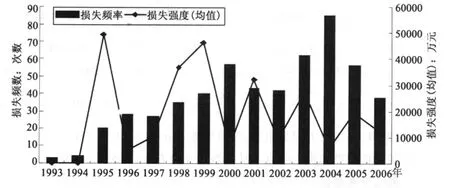
图1 先验估计用数据:中国商业银行内部欺诈年度损失

鉴于所收集的2009－2011年损失数据较少，难以反映当年银行内部欺诈损失实际情况，本文采用1994－2008年的899件损失事件，结合λ分布的先验信息，得到参数λ分布的后验分布p(λ|x)～Γ(a+t，b+n)，其中，t=899，n=15，得到泊松分布p(λ)参数λ的贝叶斯估计后验均值，因此操作风险损失频数服从泊松分布 p(59.8231)。

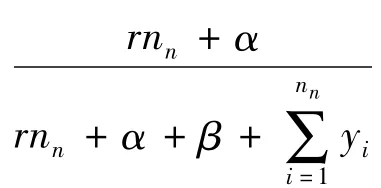
3.损失强度分布估计

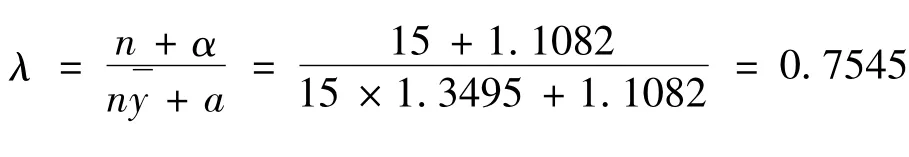
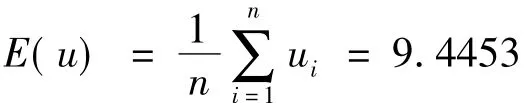
4.联合分布模拟

利用历史损失数据得到损失频率和损失强度的先验分布，然后利用新近数据结合先验分布得到后验分布，再基于后验分布得到总体分布的参数估计值，得到发生频率和损失金额的统计分布，就可以对联合分布函数进行蒙特卡罗模拟［9］，从而进一步估计未来的操作风险损失值。图2－图5为用R模拟1000次的年度商业银行操作风险内部欺诈损失。其中，图2为损失频率服从泊松分布，损失强度服从对数正态分布的模拟情况，图3为损失频率服从泊松分布，损失强度服从极值分布的模拟情况，图4为损失频率服从负二项分布，损失强度服从对数正态分布的模拟情况，图5损失频率服从负二项分布，损失强度服从极值分布的模拟情况。通过比较可以看出，损失频率分布不同导致的模拟结果相差不大，因为两种分布得出的1000个损失频率随机数类似，从而在相同损失强度分布下，模拟的损失分布比较类似。但从表3可以看出，损失频率采用负二项分布，无论在损失强度服从对数正态分布的情况下还是极值分布的情况下，负二项分布模拟的总体损失分布都略高于采用泊松分布的。而损失强度分布不同，对模拟结果有一定影响，在假设损失强度服从对数正态分布的情况下，损失除了尾部分布比较接近外，都要略小于极值分布。

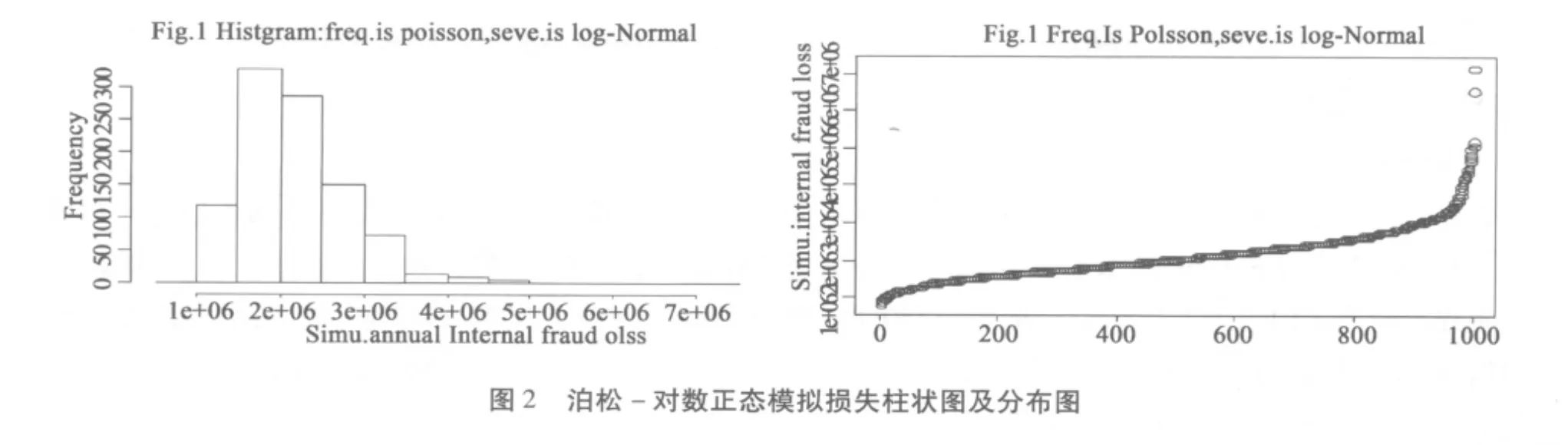
图2 泊松－对数正态模拟损失柱状图及分布图

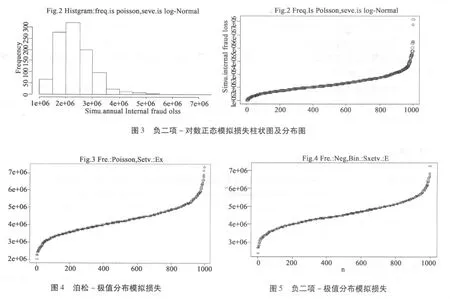
由表3可知:首先，采用几种分布得到的操作风险具有较好的一致性，特别是在巴塞尔新资本协议要求在一年展望期99.9%的置信区间下，从一定程度上验证了这几种分布都是能较好刻画操作风险分布的方法。其次，极值分布对损失强度的模拟的尾部较好，极值理论在刻画损失的尾部具有独特的优势。

表3 中国商业银行内部欺诈年度损失模拟比较 单位:亿元

五、结 论

贝叶斯推断的主要特点是使用先验分布，而在得到样本观测值后，由与先验分布提供的信息，得到后验分布。这一后验分布综合了样本与先验信息，组成较完整的后验信息，这一后验分布是贝叶斯推断的基础，而损失分布法只以样本提供的信息在一定统计模型下作统计推断，因此损失分布法对样本量较大的样本有较好的统计推断效果，而贝叶斯推断由于利用了先验知识，因而对小样本一般也有较好的统计推断效果。

本文利用操作风险常采用的损失频率分布(泊松分布和负二项分布)和损失强度分布，结合先验信息，推断后验分布。结果显示拟合效果比较好，能够准确的度量操作风险。采用不同的分布对操作风险的结果影响不大，说明这几种损失分布选择都是比较有效的，银行要有效地利用先验信息，选择模型分布，并利用实际数据分析模型。

由于中国商业银行有关操作风险事件的数据积累年限不长，数据不多，应用贝叶斯推断可以基于样本、结合先验信息做出统计推断，可以较好地解决数据不足的问题。同时后验信息可以作为今后的先验信息，结合历史数据对先验信息进行修正，随着时间的推移，数据的不断积累和事态的发展变化对先验信息进行不断修正，使分布不断逼近客观事实，对操作风险的度量能不断深化和完善。

由于中国商业银行操作风险事件类型分布极不均衡，本文仅分析了一种历史损失数据较多的事件类型，实际上，正是由于贝叶斯分析具有的特点，在利用先验信息的情况下，可以综合考虑多种事件类型或业务线的损失分布情况，并研究其相关性，这是未来需要深入的方向。

［1］张宏毅，陆静.基于损失分布模型的操作风险相关性及算法［J］.重庆大学学报(自然科学版)，2007，30(5):131－134.

［2］CORNALBA CHIARA，GIUDICI PAOLO.Statistical Models For Operational Risk Management［J］.Physica A.2004，38:166－172.

［3］EVERITT S BRIAN.The Cambridge Dictionary Of Statistics(Third Edition)［M］.New York:Cambridge University Press，2006.

［4］HELLER BEMERKUNGEN，WANG MEI.Posterior Distribution For Negative Binomial Parameter Using A Group Invariant Prior［J］.Statistics ＆ Probability Letters，2007，77:1542 －1548.

［5］DUVALL M RICHARD.A Bayesian Approach To Negative Binomial Parameter Estimation［EB/OL］.http://www.casact.org/pubs/forum/99wforum/wf99377.pdf.

［6］卢安文，任玉珑，唐浩阳.基于贝叶斯推断的操作风险度量模型研究［J］.系统工程学报，2009，24(3)3:276－292，349.

［7］NASCIMENTO F FERNANDO，GAMERMAN DANI，HEDIBERT F LOPES.A Semi-parametric Bayesian Approach To Extreme Value Estimation［EB/OL］.http://faculty.chicagobooth.edu/hedibert.lopes/research/pdf.

［8］VALLE L DALLA，GIUDICI PAOLO.A Bayesian Approach To Estimate The Marginal Loss Distribution In Operational Risk Management［J］.Computational Statistics ＆ Data Analysis，2008，52:3107 －3127.

［9］樊欣，杨晓光.我国银行业操作风险的蒙特卡罗模拟估计［J］.系统工程理论与实践，2005，22(5):44－48.