火箭助推无人机起飞段发射动力学建模与分析
马 威,马大为,胡智琦,庄文许,王新春
(1.南京理工大学机械工程学院,江苏 南京210094;2.北京控制工程研究所,北京100190;3.中国船舶重工集团第七二四研究所,江苏 南京210094)
0 引言
纵观国内外无人机的发展现状,无人机在军事领域的应用日益广泛,正在成为现代高科技战争中不可或缺的武器。无人机具有隐蔽性好、生命力强、造价低廉、不惧伤亡、起降简单和操作灵活等诸多优点而备受各国青睐[1-2]。无人机最通用也是最成功的发射方法之一是火箭助推发射方式,无人机安装在导轨发射装置上,在助推火箭推力的作用下飞离发射装置,助推火箭在很短的时间内向无人机提供大量的机械能,使其在火箭脱落前达到保证无人机安全飞行的高度和速度,之后由机上发动机完成飞行任务[3-4]。
无人机在发射过程中虽然在发射导轨上的时间非常短,但是它在发射导轨上的运动和受力情况是复杂的,在发射装置设计和研制的初期阶段结合计算机手段,对发射系统进行发射动力学分析,可以大大缩短研制周期,降低研制成本,提高研制质量[5-6]。因此,以某无人机火箭助推箱式发射系统为物理原形,建立了发射动力学和运动学模型,并结合Matlab软件完成了该型无人机发射段数值仿真分析,求得其离轨运动参数,分析其安全发射问题。
1 发射模型特点及模型假设
根据无人机型号的战术要求,采用箱式发射技术[7-8]。无人机在导轨上的运动由两部分组成:在轨段(前后滑块均在导轨上的运动);离轨段(前滑块已滑离导轨后滑块仍在导轨上运动)。当其前滑块离开滑轨后,无人机会绕其后滑块转动,于是产生转动角及转动角速度,即下沉角与下沉角速度。为了研究问题的需要,在此作如下假设:
a.无人机和发射箱导轨为刚体,在运动过程中其形状、质量和质心都不发生变化,认为无人机在一个纵向平面内运动,发射装置的导轨在一个平面内,即导轨无弯曲扭转变形。
b.发动机推力在发射过程中恒定不变,不考虑发射箱和无人机的振动。
c.不考虑推力偏心和推力偏心矩,即发动机推力始终通过无人机质心,同时不考虑风力的影响。
d.在固定地面上发射无人机。
2 发射动力学数学模型
2.1 发射动力学和运动学方程组
设发射架导轨上前滑块滑行长为L1,后滑块滑行长为L2。如图1所示,建立离轨坐标系OXYZ,取初始发射时刻后滑块与导轨的接触点为坐标原点O;OX轴沿导轨方向,指向发射方向为正;OY轴包含在OX轴的铅垂平面内,垂直OX轴指向上为正;OZ轴按右手定则确定。在此,根据达朗贝尔原理和动静法的形式,来描述无人机发射段的动力学模型[9]。
采用的方程组形式为:

→■F,→■Mo(F)分别为作用于质点系上的主动力和力矩;→■N,→■Mo(N)分别为作用于质点系上的约束力和力矩;→■Q,→■Mo(Q)分别为作用于质点系上的惯性力和力矩。
2.1.1 无人机在轨段发射动力学模型
当前滑块沿OX轴方向滑行距离小于L1时(即前滑块尚未脱离导轨),则无人机在导轨上作直线运动,其受力分析如图1所示。

图1 无人机在轨段的受力分析
则得无人机的运动方程为:

F=μ(N1+N2)=μ(G cosθ0-P sinδ);vx为导弹沿OX轴方向运动速度;vy为导弹沿OY轴方向运动速度;x为导弹沿OX 方向的运动距离;y为导弹沿OY方向的运动距离;P为发动机推力;G为导弹重力;θ0为导弹发射角(假设与导轨仰角相等);μ为前后滑块与滑轨的摩擦系数;m为无人机质量。
对无人机的质心求力矩得:

与N1+N2=G cosθ0-P sinδ联立,可得无人机在导轨上运动所受的支撑力为:

L3,L4为无人机前、后滑块到质心的距离;L5为导轨面到无人机纵轴的距离;L6为前后滑块间的距离,且L6=L3+L4。
2.1.2 无人机离轨段发射动力学模型
当后滑块沿OX轴方向滑行距离大于L1且小于等于L2时,则无人机作刚体平面运动,其受力分析如图2所示。

图2 无人机离轨段的受力分析
无人机作刚体平面运动时,假设无人机离轨过程中与滑轨有且只有一个接触点,即o点,忽略滑块的大小和质量,设点C为无人机质心,点o为滑轨与无人机接触点。
如图3所示。由基本力学知识可知:

图3 运动的合成与分解

质心动力学方程为:

由式(4)可得o点加速度为:

而˙voy=0,则有:

联立式(5)和式(7),得:

可得:

绕质心的转动方程为:

即得:

代入式(8)得:

综合式(8),式(9),式(11),得到无人机运动方程组为:

θ为无人机俯仰角;ω为俯仰角速度;Jc为导弹绕OZ轴的转动惯量;N为导弹所受支持力,由式(12)得到。
2.2 无人机发射安全分析
为了使无人机从导轨上滑离后不与发射箱相撞,在结构设计中,必须保证机箱间有足够的让开距离。最小让开距离的确定是发射动力学研究的基本问题之一,对活动载体小射角尤为重要。机箱间的碰撞是由以下几种因素引起的:无人机在重力、推力及其他因素作用下产生的下沉、发射装置的振动和载体的运动。当无人机前支点离开发射架后,此时会有头部下沉现象,一直到无人机尾段完全离开发射箱,在此期间由于无人机相对发射箱的转动,无人机的尾部A点最有可能与发射箱相撞,其相对位置如图4所示。

图4 无人机与发射箱的相对位置
由图4所示的几何关系,可以得到无人机尾部到无人机发射轴的距离yA,令Δθ=θ0-θ,则有:
当Δθ<0时,yA=RAsin(Ψ-Δθ)+yr;当Δθ>0时,yA=RAsin(Ψ+Δθ)-yr。
可以得到不与发射架相碰的条件为:

确定发射装置后,就可以确定R,Ψ的值。前面通过对无人机相对于发射坐标系的运动微分方程进行积分,就可以得到无人机质心的相对位移yr,由此就可以求得无人机是否安全发射。
3 仿真及分析
3.1 无人机在导轨上的运动规律
取无人机的导轨长度为2.8 m,发射倾角为15°,则得出无人机在导轨上运动的位移、速度和俯仰角的变化规律,如图5~图7所示。

图5 无人机的位移
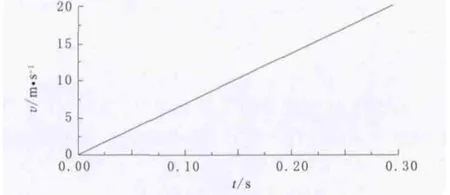
图6 无人机的速度
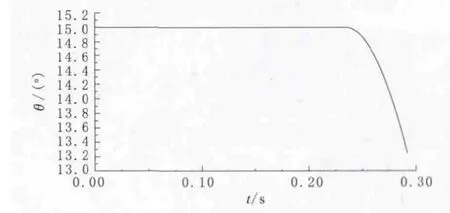
图7 无人机的俯仰角
3.2 无人机离轨时的特性参数
分别取不同的滑轨长度和发射倾角,得到无人机离轨时特性参数如表1和表2所示。表1导轨长度分别取2.4 m,2.6 m,2.8 m和3 m,发射倾角取θ0=15°;表2发射倾角分别取15°,20°,25°和30°,导轨长度取2.8 m。
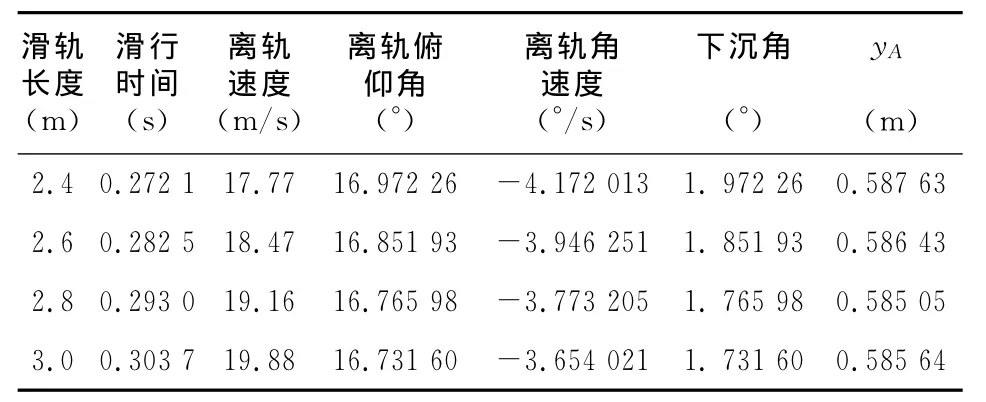
表1 不同滑轨长度的离轨特性参数

表2 不同发射倾角的离轨特性参数
计算结果表明,不同的滑轨长度和发射倾角可分别获得不同的离轨速度、离轨俯仰角和让开距离,离轨过程中出现了不同程度的下沉角。随着滑轨长度的增大,离轨时间增加,离轨速度增大,离轨俯仰角速度减小,下沉角减小;随着发射倾角的增大,离轨时间增加,离轨速度减小,而离轨俯仰角速度的绝对值先减小到0再增大,下沉角先减小再增大,所以无人机的发射角增大到某一定值时,无人机的俯仰角速度最小,下沉量也最小,有利于无人机的发射。无人机发射过程中,无人机尾部到无人机发射轴的距离yA都小于机箱间的让开距离R,因此,无人机能安全发射。
4 结束语
通过建立无人机发射动力学数学模型,利用Matlab软件对其发射过程进行仿真分析。仿真结果表明,无人机离轨速度、角速度、俯仰角、下沉角以及让开距离与导轨长度和发射倾角有关。由于无人机离轨角速度、下沉角会对无人机的初始运动参数产生一定的影响,因此,应对发射初始参数做出适当的修正;同时为减小离轨段的下沉角和下沉角速度,可从增加导轨长度或者增大发射倾角两方面考虑。
[1] 杨 旭,王鹏基,杨 涤.无人机起飞段航迹控制方案设计与数学仿真[J].战术导弹技术,2004,(4):42-46.
[2] 何 庆,刘东升,于存贵,等.无人机发射技术[J].飞航导弹,2010,(2):24-27.
[3] 刘保柱,苏彦华,张宏林.Matlab7.0从入门到精通[M].北京:人民邮电出版社,2011.
[4] 李 浩,肖前贵,胡寿松.火箭助推无人机起飞发射段建模与仿真[J].东南大学学报,2010,40(Z1):136-139.
[5] 荣 辉,李 冬,殷堂春.基于Matlab无人机数学模型仿真分析与研究[J].科学技术与工程,2008,8(6):1510-1535.
[6] 田新锋,薛 鹏,李红泉.某无人机火箭助推发射研究[J].宇航计测技术,2012,32(2):30-32.
[7] 陈进宝,张晓今,张管飞.地空导弹发射动力学建模与仿真研究[J].弹簧与制导学报,2010,40(1):65-71.
[8] 廖莎莎,吴 成.机载导弹发射动力学建模与虚拟样机仿真[J].北京理工大学学报,2011,31(9):1013-1017.
[9] 薛明旭.战术导弹发射动力学与仿真[D].西安:西北工业大学,2004.

