一种新型宽轮式越野机器人
高永生,王 钢,赵 杰,朱延河,徐 昊
(1.哈尔滨工业大学机器人技术与系统国家重点实验室,黑龙江 哈尔滨 150001;2.哈尔滨工业大学信息与通信工程研究所,黑龙江 哈尔滨 150001;3.天津大学电气与自动化工程学院,天津 300222)
0 引言
越野机器人采用遥控、自主或半自主等方式完成地面运动,具有广阔应用前景和军事价值,正受到越来越多的关注和研究[1-2]。国内外多位学者和研究机构进行了面向野外环境的越野机器人研究。相对于前轮转向后轮驱动的机器人,四轮驱动更适于沼泽地、泥地和坑等较复杂的野外场地[3]。国内的沈阳自动化研究所、中国科技大学、南京理工大学等单位对越野机器人的本体结构、运动规划和远程控制等方面进行了广泛研究[4-5]。轮式越野机器人采用全轮式移动、对称结构,能提供良好的机动性和可靠性。通过研究轮式越野机器人的宽轮式结构、中间轴结构和差动式转向方式等结构特性,获得机器人转向稳定性、不同路面上行驶平稳性和在各种路面之间转换行驶平顺性。
1 结构性能分析与设计
1.1 越野性能分析
轮式越野机器人的性能受到驱动力、爬越横斜坡和通过小障碍物的影响。
当机器人在长坡上等速爬坡行使时,车身重量就会依据其重心位置产生不同的坡度阻力。机器人驱动力受到坡度阻力影响。
当机器人沿着横斜坡行驶时,若坡角大于某一定值,则一侧车轮的地面反作用力等于零,机器人失去横向稳定性,出现侧翻或侧滑问题。
机器人在野外行进时遇到的几何形小障碍物对越野性能的影响较大,具体情况为:一是车体的底部碰到凸形障碍,于是机器人被悬起而失去通过性;二是机器人的前后突出部碰到较大凹形障碍,被卡住而不能通过[6]。
1.2 越野机器人结构设计
根据以上越野性能分析,设计的轮式越野机器人的整体结构为前后、左右对称的形式,采用四轮驱动、宽轮式移动机构、差动转向以及特殊的中间轴连接方式。
机器人车轮可以分为前后两组,每一组都有2个外轮,它们套在同一个驱动内轮上面组成一组车轮,外轮完全包围内轮,前后两组车轮是通过中间轴连接。控制部分全部在内轮里面,外观如图1所示。

图1 宽轮式越野机器人整体结构
中间轴具有一个自由度,通过中间轴凸台(两端都有)将中间轴固定在机器人前后内轮上面,如图2所示。由于采用了中间轴的连接形式,使机器人的整体结构更加对称,同时机器人的重心降低,在运行的过程中,获得更好的稳定性。在穿越碎石路面的时候能够使前后两组车轮先后绕中间轴旋转,克服崎岖不平的地形,并且不用过多考虑机器人自身位姿。

图2 中间轴结构
机器人的传动系统采用变速箱减速后经内啮合齿轮输出,传动平稳,耐冲击性好,电机套件、控制板和驱动板全部固定在控制盒内,再装配进机器人的内轮,如图3所示。

图3 机器人传动系统
2 宽轮式越野机器人运动学建模
2.1 运动学分析
2.1.1 小车的模型近似等价为两轮车模型
设定小车的2个左侧车轮有相同的转角和速度,2个右侧车轮有相同的转角和速度,车体运动简化为两轮车运动结构。运动与分析如图4所示。
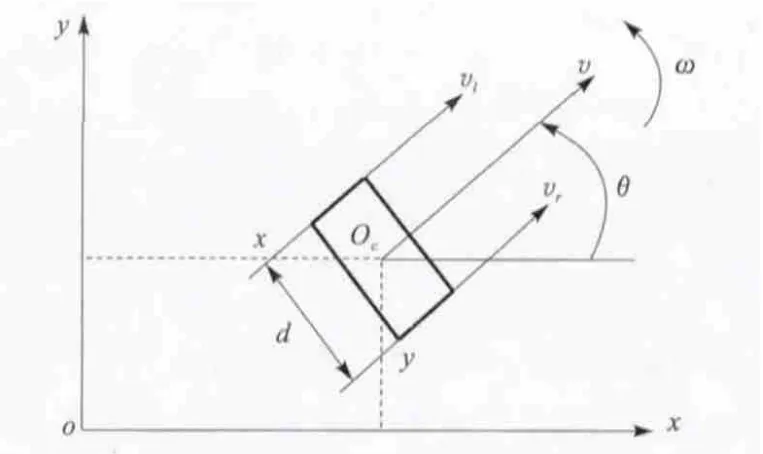
图4 两轮式机器人车的运动学分析
由图4的运动学分析,按照几何关系以及运动学关系可以推导出:
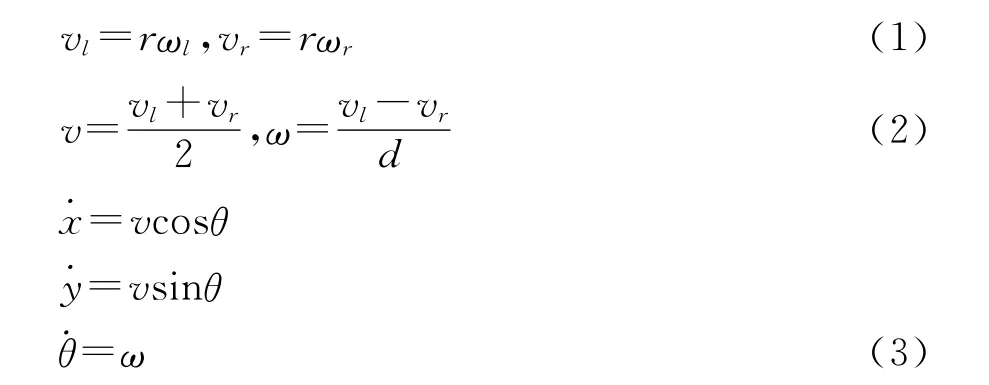
v,ω为机器人车体中心的瞬时线速度、角速度;vl,vr为机器人左右两侧轮组的瞬时速度;ωl,ωr为机器人左右两侧轮组的瞬间角速度;d为机器人两轮质心的距离;r为机器人车轮半径为机器人的速度v沿x坐标方向的分量为机器人的速度v沿y坐标方向的分量;θ为机器人的速度方向与坐标方向的夹角。
由于车轮只做纯滚动无滑动,可得约束条件为:

由式(6)可知,通过控制机器人两车轮组的角速度,就可以控制机器人车的运行速度和转向角速度,也就是说,可以通过控制车轮组的加速度来控制机器人的运动姿态。
通过几何关系,可以推导出机器人的偏转角速度ω和转弯半径R满足以下关系式:

由式(7),式(8)可以得出本体运动的3种可能的情况:
a.当vl=vr时,机器人车体(中心O)的线速度v=vL=vR,角速度ω=0,转弯半径R→∞,这时机器人作直线运动。
b.当vl=-vr时,机器人车体(中心Oc)的线速度v=0,角速度ω=-2vl/d,转弯半径R=0,这时机器人车体绕其几何中心Oc转动,实现机器人的原地转向。
c.当vl≠vr时,机器人车体(中心Oc)的线速度v=(vL+vR)/2,角速度ω=(vl-vr)/d,转弯半径R=d(vl+rr)/2(vl-rr),这时机器人绕点Oc作半径为R的转动。
通过以上的分析可以看出,控制机器人左右两侧轮组的速度,就可以实现机器人沿着任意设定的轨迹行走。
2.1.2 四轮驱动
每个轮子独立驱动,运动与分析如图5所示。

图5 四轮驱动越野机器人运动学分析
图5中,XOY为固定参考坐标系;xocy为通过机器人几何中心的相对坐标系;xioiyi为固连在车轮组上的坐标系(i=1,2,3,4);oc为机器人车体几何中心;oi为机器人第i个车轮组回转中心(i=1,2,3,4);θ为机器人相对坐标系xocy的x轴与X 轴的夹角;L为通过机器人几何中心与各个轮组回转中心之间的距离;αi为x轴与车辆中心和第i个车轮组的回转中心线之间的夹角(i=1,2,3,4);(x,y,θ)为机器人几何中心oc在地面坐标系中的位姿;ωi为各个车轮的转动角速度;θ0为前轴外转向轮转角;θi为前轴内转向轮转角;r为车轮半径。

式(9)为4个车轮驱动情况下机器人车体的运动学模型,能够通过控制4个车轮组的转速控制机器人本体速度和姿态。
2.2 仿真分析
为了优化宽轮式越野机器人的运动性能,将机械结构Pro/E图导入到ADAMS中,仿真模拟系统的运动和动力特性,并根据仿真结果优化系统。
仿真过程中做如下假设和约定:机器人所作运动为平面运动,整个机器人本体视为一个刚体,车轮视为刚体轮,不考虑轮胎与地面侧向滑动的情况,即轮胎无滑动,作纯滚动运动。
2.2.1 直线行走仿真
仿真实现机器人4个车轮的轮槽为整体“人”字形,在平坦路面上前进或后退。其位移如图6所示(图中粗虚线为X方向运动,实线为Y方向运动)。
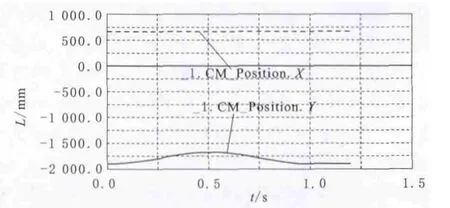
图6 前进后退的直线运动轨迹
在ADAMS里面将机器人的直行运行状态设置成沿着X正方向先前进,再后退,分别检测X,Y 2个方向的位移量。从图6可以看出,在运动过程中Y方向的位移没有变化,这说明机器人在运动的时候Y方向轨迹没有偏离,运行良好。
2.2.2 90°转向运动仿真
ADAMS仿真的时候先是在XOY平面上沿X正方向前进,运动1s后,转向90°后再沿Y负方向行驶1.5s。具体的轨迹曲线如图7所示。曲线反映了机器人在X,Y方向上的位移变化关系,图中下部的实线和虚线分别为转向前X,Y方向运动,上部的虚线分别为转向后X,Y方向运动。

图7 转向90°运动轨迹
根据式(9),可得:

式(10)中各参数的含义与式(3)相同。通过运动学方程得到的数值基本上与仿真曲线相吻合。
2.2.3 小半径回转仿真
机器人在YOZ平面以小半径回转,将机器人的4个外轮分为左右两组,每组外轮的运动的速度相同,方向相反,可以完成小半径回转。如果两组轮子的速度相等,方向相反就可以实现零半径回转。小半径回转的位移曲线如图8所示。图8中,以起点划分,起点为零的直线(实线)是外轮沿X轴的位移,起点接近100mm的正弦曲线(长虚线)是外轮沿Y方向的位移,起点稍大于175mm的正弦曲线(虚线)是外轮沿Z轴的位移,起点稍大于200mm的是外轮的总的位移曲线(矢量和)。因为机器人是一个很小的半径做回转运动,所以位移曲线是近似正弦线。如果机器人以坐标原点为回转中心,则位移曲线将会是标准的正弦。
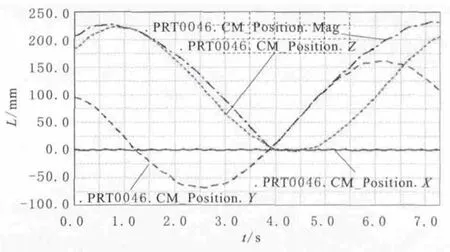
图8 小半径回转运动仿真
2.2.4 越障仿真
在越障仿真中,机器人经过一个很短的凹坑路面,由于中间轴的随动作用,机器人就会自动调整位姿来适应地形的变化。仿真是在YOZ平面内沿Z轴负方向运动。
图9a中水平直线是中间轴在X方向的位移,以零为起点在末端向下倾斜的曲线是中间轴在Y方向的位移,起点大于零的一条斜直线是中间轴在Z轴方向的位移。图9b中两条水平直线几乎重合,分别是中间轴在X,Y方向的位移,斜直线是中间轴在Z方向的位移。从两图的对比可以看出来,中间轴没有随动自由度的机器人在遇到凹坑的时候,不能自动调节车体位姿以适应地面,表现在图9a中就是Y方向的末端(凹坑尽头)位移曲线有偏移,即机器人在Y方向上有移动,而图9b所显示的一直是直线状态。这说明中间轴有随动作用的时候,机器人具有更好的地面适应能力。
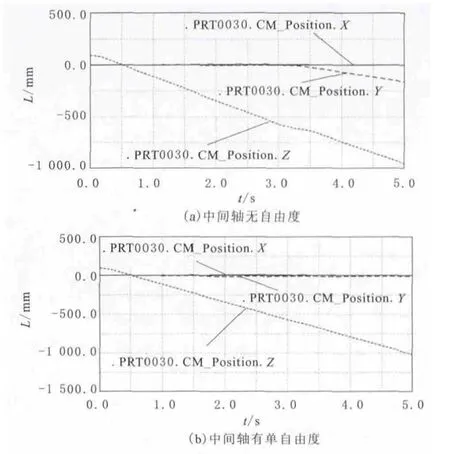
图9 机器人越障仿真
3 实验研究
搭建实验系统如图10所示。左上为上位机控制系统,用于发送处理控制指令;右上为无线收发模块,一块连接上位机,另一块连接驱动控制板;左下为驱动控制板,接收来自上位机或者是无线模块的指令,直接控制右下的机器人,并将编码器的信号反馈给控制器。所设计的轮式越野机器人的车体宽度为192mm,轮半径为60mm。

图10 轮式越野机器人试验系统
轮式越野机器人的直线行走实验中,4个电机均为正向转动,驱动机器人直线前行。机器人沿直线行走2400mm,测量偏移的距离。经过10次试验的测量,机器人的最大偏移是23mm。可见机器人的直线运动性能较理想。
轮式越野机器人转向试验中,分左右两组控制4个电机。控制左侧电机反向转动,右侧电机正向转动,实现机器人的逆时针原地转向。反之,机器人就顺时针转向。机器人逆时针旋转实验如图11所示。每张图片均为45°角度间隔,机器人能够平顺转向。

图11 轮式越野机器人小半径回转
轮式越野机器人的越障实验中,在机器人前进的路面上有35mm高的障碍物,机器人越过遇到的小障碍物并且保持原先的前进状态,如图12所示。这个过程中,主要是由于中间轴的作用,使机器人在越障碍物的时候,能够保持住原先的运动方向和状态。通过实验验证,机器人所能够爬越的最大障碍物为轮子直径的1/2。

图12 轮式越野机器人越障实验
4 结束语
设计了一种面向野外环境的对称式宽轮越野机器人。通过具有单自由度的中间轴连接结构,提高了地面适应能力和越野能力。建立了机器人运动学模型,并通过ADAMS软件仿真和实验验证机器人的行走、小半径回转和越野能力,表明机器人具有高机动性、机构简单和方便控制等优点。
[1]李 磊,叶 涛,谭 民,等.移动机器人技术研究现状与未来[J].机器人,2002,24(5):475-480.
[2]章小兵,宋爱国.地面移动机器人研究现状及发展趋势[J].机器人技术与应用,2005,(2):19-24.
[3]王鸿鹏,赵 磊,杨 云,等.面向高速精确漂移的轮式移动机器人建模与分析[C].第三十一届中国控制会议,2012.5064-5069.
[4]尚伟燕,邱法聚,李舜酩,等.复合式移动探测机器人行驶平顺性研究与分析[J].机械工程学报,2013,49(7):155-161.
[5]陶卫军,欧 屹,冯虎田,等.多功能地面移动机器人设计与分析[J].南京理工大学学报(自然科学版),2010,34(6):759-764.
[6]Noah Z.United states marine corps/robotics technology consortium cargo unmanned ground vehicle[C].AUVSI Unmanned Systems North America Conference,2011.1335-1341.

