基于运行数据的变桨力矩偏差信号处理方法研究

李凤格，卢晓光，李 豪，吴 莉

（1.许昌许继德理施尔电气有限公司，河南 许昌 461000；2.许继集团有限公司，河南 许昌 461000；3.许继电气股份有限公司，河南 许昌 461000）

0 引言

变桨控制是风力发电机调节风能的吸收率的主要方式之一［1］，变桨力矩是变桨电机提供给变桨变桨机构的动力源［2］。对变桨力矩的控制，关系到风机运行的稳定性和安全性［3-4］，所以，在风机运行时必须对风机进行有效的监控。变桨力矩随着叶片在风轮平面内的位置变化，呈现出周期性变化趋势［5-6］。对于3叶片风机，3个桨叶在同一时刻会以120°方位角的差值分布于风轮平面内，所以3个叶片变桨力矩会有一个以风轮转速为周期的周期性变化的不同步偏差，在监测变桨力矩偏差时，如果简单监测同一时刻3个桨叶变桨力矩的不同步值，必定导致偏差扩大化。为更好地使监测结果反映3个变桨电机输出变桨力矩的实际不同步值，以风场运行风机采集数据为依据，分析了变桨力矩受力情况；设计了滤波器进行必要的数据处理；并引入风轮转速这一参数，来区别不同转速下变桨力矩变化周期的变化。通过上述分析，改进数据处理策略，最终解决了风场经常误报变桨力矩不同步告警这一现象。

1 变桨力矩特性分析

1.1 克服风作用于叶片力的气动变桨力矩

风机叶片的所有叶元受力，作用于变桨轴线的扭矩之和，构成气动变桨力矩部分［7］。因风剪效应的存在，风速会随着离地面高度的增加而增加，气动变桨力矩也会随着风轮旋转方位角的改变而周期变化，变化周期和风轮旋转频率相同。因叶片设计时，要求尽量使变桨轴线和叶元的受力轴心重合，所以，气动变桨力矩在整个变桨力矩中所占比例不大。

1.2 克服变桨轴承摩擦力的摩擦变桨力矩

摩擦变桨力矩是变桨电机克服的主要力矩。因径向力轴向力及径向弯矩会随着风轮旋转做周期性变化，这个变化规律是复杂的。现以最简单的假设模型说明问题，假设现在只有叶片重力对轴承有作用力。那么，在竖直向上方位角处，轴承受到指向轮毂中心的轴向力；在竖直向下方位角处，轴承受到背离轮毂中心的轴向力；当方位角在水平方向时，叶片重力转化为径向弯矩，这个对摩擦力的增加作用最明显。bladed仿真模型可知，摩擦力中的弯矩所增加的摩擦力起决定性作用，在变桨力矩中所占比重最大。所以变桨力矩必定以风轮转速为频率，存在较大的周期波动。

1.3 惯性变桨力矩

由于叶片预弯等，在不同变桨角度，叶片对变桨轴线的变桨惯量会有所不同，但由bladed仿真输出上看，其变化不大。在变桨速度改变的时刻，由于巨大叶片惯量的加速度力，惯性力会占据变桨力矩的主要成分。因主控中是集中下发变桨速度，所以在变桨速度改变过程中，3个桨叶的惯性变桨力矩会同时改变，不会出现规律的周期性变化。

2 现场数据处理方法分析

经上述变桨力矩特性分析可知，变桨力矩在风机运行过程中会出现一个周期和风轮转速相关的周期性波动。所以，在判断3个桨叶变桨力矩不平衡时，需要进行低通滤波，以消除叶片所处方位角不同的影响。因原始采样数据的特性中有周期性波动成分，在选取判断值时用数据的有效值更合理。基于此，不同步判断数据处理框架搭建如下：现场数据的采样频率为0.01s，采集变桨力矩数据，采集到的数据的平方，经一个低通滤波器滤波，再通过积分器求取平方根，最终得到变桨力矩的有效值。将3个桨叶的变桨力矩有效值比较，取最大差值，当差值超过告警值时，进行告警。

2.1 一阶滤波器的设计及滤除效果分析

一阶滤波器截止频率选取依据风轮转速进行。齿轮箱开始高速供给润滑油的发电机转速为400r／min，折合成风轮侧转速的频率为0.06Hz。低通滤波器的截止频率至少应低于此频率，考虑到风轮会在更低频率下运行的情况，确定滤波时间常数为10 s，其截止频率为0.016Hz。滤波器可表示为：

τ为时间常数，此处取10；s为拉普拉斯算子。

在PLC中，需要对连续传递函数进行离散化处理。离散化可使用双线型变换进行［8］，但考虑到采样频率为0.01s，经离散化处理后，传递函数为：

y（k）为当前输出；y（k-1）为前一时刻输出；x（k）为当前输入。

现以幅值为0.5的正弦信号对滤波器滤波效果进行Matlab仿真测试，信号频率设置与风轮额定转速频率相同，都为1.753rad／s。结果如图1所示。

图1 高频信号滤波效果

a.经滤波器过滤，以风机额定转速频率变化的信号可衰减到原始信号幅值的4%左右，周期性信号得以滤除。

b.离散滤波器输出和连续滤波器输出几乎完全重合。说明离散化滤波器可以使用。

当风轮转速较低时，再次测试信号通过滤波器的效果，结果发现，对信号的过滤效果明显减弱。例如，当发电机转速为200r／min时，风轮转速频率为0.195rad／s，则仿真结果如图2所示。

图2 低频信号滤波效果

由图2可知，在电机转速以200r／min左右变化时，信号如果和风轮转速频率相当，则滤波器的滤除效果会明显降低，以风轮转速频率变化的信号可衰减到原始信号幅值的50%左右，虽然此频率还在滤波器截止频率以上。

以上分析可以看出，当3个桨叶以相差120°的方位角运行时，如果变桨力矩存在以风轮转速为频率的周期性波动，那么在较慢的风轮转速下，很容易产生3个变桨力矩不同步的现象。

我国金融利率市场遵循“先农村后城镇，先贷款后存款”的规律，在2015年正式放开城镇居民的存款利率，但对贷款利率仍然实行严格的管控。目前，农村信贷资金紧张，农村金融改革乏力，严重影响了乡村振兴战略的实施。要逐步放宽农村信贷利率浮动区间，满足农业建设对信贷资金的需求。同时要建立农村金融市场风险投资机制，完善农村金融财政补贴政策，加强农业担保基金管理，设立农村共管基金，从而增强农村金融市场的资金周转量[6]。

结合风机运行特性可知，变桨不同步容易出现在小风及大桨距角的情况下。特别是小风和大桨距角同时出现（80°～90°桨距角时），风轮几乎不动，变桨又没有完成，那样的时刻报出不同步是很可能的。对于继续增加滤波时间以换取更低风轮转速下的滤波效果这一可能性，经分析是不可取的，因为更大的时间常数意味着更长的延时。

2.2 现场数据分析

利用上述数据处理过程及2.1节设计的滤波器，对现场变桨力矩进行数据处理及采样。PLC数据滤波周期为0.1s保存一个数据，因数据发送及传输过程中的丢失等原因，不能保证严格的每个数据为0.1s，但并不影响利用数据进行分析。

图3为滤波工具记录下的一段风机起动运行到停止，整个变化过程中3个桨叶变桨力矩的变化情况；图4为对应桨距角的变化情况；图5为对应的变桨力矩有效值偏差计算情况。

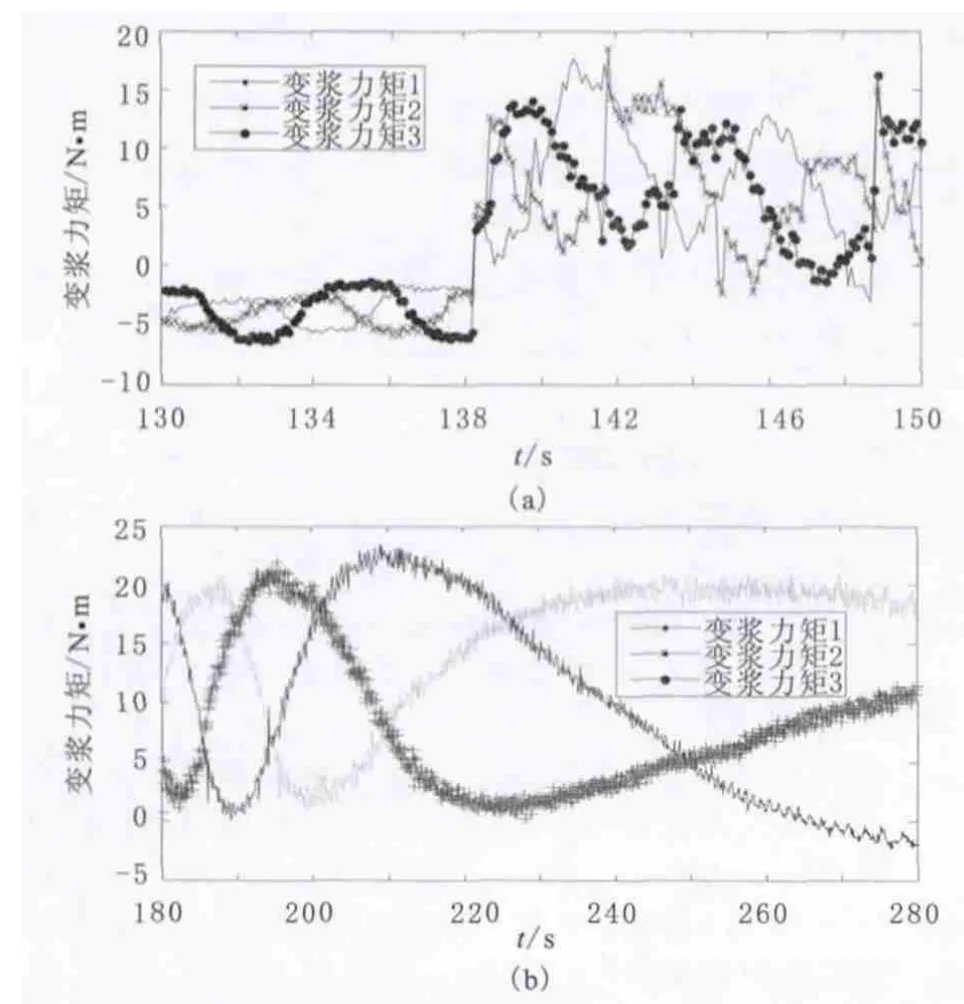
图3 变桨力矩

由图3～图5可知：

a.每当变桨速度跳转过程（图3a横坐标138～139时段），就会发生变桨力矩的一个突变，这个突变是惯性力作用的结果。3个桨叶同时突变，不会影响不同步。

b.图4横坐标120处，桨距角0度不动，3个桨叶变桨力矩以风轮转速频率周期波动，这时很小，只是风剪切的影响，因不变桨，摩擦力不参与其中，其变化周期与风轮转速变化周期同步。

图4 变桨角度

图5 变桨力矩有效值偏差

c.图3b横坐标180～280处，随着变桨角度增加，风轮转速减小，周期性波动的周期随之变化。对于单个叶片，随着转换周期拉长，摩擦力及风载荷，变化效果被充分体现出来，周期变化幅度被同时拉大，这一点会有限度，加大到接近静态水平即停止。

d.当桨距角接近90°，风轮转速很低，接近停止，变桨力矩差距几乎保持不变，此时因滤波器作用消失，最容易产生不同步告警。

图6为滤波工具记录下的一段大风运行工况中3个桨叶变桨力矩的变化情况；图7为对应桨距角的变化情况；图8为对应的变桨力矩有效值偏差计算情况。因变桨控制策略采用的集中变桨控制，3个桨距角有同步控制过程，所以在正常情况下3个桨距角变桨角度几乎是重合的，图4和图7中3个变桨角度变量只显示一条曲线，是曲线覆盖的表现。由图6～图8可知：

图6 大风工况变桨力矩变化情况

a.变桨速度每变化一次，3个变桨力矩在惯性力的作用下会同步较大幅度变化一次，变化幅度取决于变桨速度的改变大小。

b.对变桨力矩做谱分析得知，其变化周期的主要能量集中部分，恰好是风轮转速的周期。

c.由于风轮转速较高，滤波作用使变桨力矩偏差很小，不会报偏差过大，其偏差如图8所示。

图7 大风工况变桨角度变化情况

图8 大风工况变桨力矩有效值偏差

3 变桨力矩偏差策略监测改进

经现场数据变化规律分析及总结，可知，风轮转速的变化可以使变桨力矩正常变化时产生较大的偏差改变，特别是在电机转速300r／min以下时，风轮转速只有0.046Hz左右，变桨力矩偏差必定会因滤波器效果减弱而增大。

图9为风场采集变桨力矩偏差信号随风轮转速变化统计散点图。由于以上原因，对变桨力矩偏差监测方法做如下改进：引入发电机转速变量，当转速在300r／min以上时，设置正常报警阈值；当转速在300r／min以下时，设置较大报警阈值。阈值的最终确定参考风场风机正常运行数据来定。由图9中数据的偏差最大值乘余量系数，即可确定300r／min以上及以下的报警阈值参数。

图9 变桨力矩偏差随风轮转速变化统计散点图

4 结束语

针对风场机组在正常运行时误报变桨力矩偏差过大的问题，借助bladed软件仿真分析了变桨力矩的变化规律，通过力学分析划分了变桨力矩的组成部分，结合风机运行情况推断了变桨力矩随风轮转速周期性变化的规律，并通过bladed仿真观察了变桨力矩这一变化规律。结合风场数据，设计了高电机转速下对变桨力矩有效值的滤波器；结合变桨力矩的组成部分的划分，分析了变桨力矩风场采集数据的主要变化诱发因素；给出了以电机转速为变量，分段确定变桨力矩偏差阈值的监测策略和变桨力矩不同步阈值的确定依据。

［1］王大为，陶学军，卢晓光.基于柔性叶片模型的独立变桨减载控制［J］.电力系统保护与控制，2012，40（16）：111-115.

［2］苏勋文，米增强，陈盈今，等.基于运行数据的风电机组建模方法［J］.电力系统保护与控制，2010，38（9）：50-54.

［3］李俊芳，张步涵，谢广龙，等.基于灰色模型的风速-风电功率预测研究［J］.电力系统保护与控制，2010，38（19）：151-159.

［4］何玉林，黄 帅，杜 静，等.基于前馈的风力发电机组变桨距控制［J］.电力系统保护与控制，2012，40（3）：15-20.

［5］崔双喜，王维庆，张新燕.大型风力发电机组无模型独立变桨载荷控制［J］.电力系统保护与控制，2013，41（5）：54-59.

［6］何玉林，黄 帅，苏东旭，等.变速风力发电机组的多变量桨距控制策略［J］.电力系统保护与控制，2011，39（15）：33-37.

［7］高文元，卢晓光，王 鹏，等.变速变桨距风机风轮的建模与控制［J］.机械与电子，2008，（9）：27-29.

［8］胡广书.数字信号处理.2版［M］.北京：清华大学出版社，2003.