一种基于瞬时频率的多普勒畸变声信号校正方法
袁仲洲,孔凡让,张海滨,胡 飞,刘 方,朱丕亮
(中国科学技术大学精密机械与精密仪器系,安徽 合肥 230027)
0 引言
声音轴承检测系统形成于20世纪80年代,采用轨边监测麦克风阵列来采集轴承运行时发出的声音,通过分析轴承声音信号来判断轴承的运行状况。这种方式可以发现轴承早期故障,系统置于铁轨旁,并不直接装载在列车上,成本低,可以置于一些关键的火车站点,每天能够监测通过的所有列车的几千个轴承,通用性好。但也存在较多的技术难点,比如由于麦克风放置位置与铁轨的不可忽略的约1m的距离,以及轴承声源移动相对麦克风存在横向速度,产生了不同于雷达等领域多普勒效应的畸变声音信号,对其进行分析和校正是进行精确的轴承故障信号特征提取和诊断的前提[1]。
20世纪90年代开始,Stojanovic M[2]等人提出了用锁相环技术(PLL)进行多普勒声音信号校正,随后Johnson M[3]等人在此基础上提出了锁相环技术与DFE算法相结合的校正方法,并将其运用在AUV与水面舰艇声纳通信中,该方法适用于通信级别的信号校正,方法本身涉及的技术较多,较为复杂;近期Dybala J[1]等人提出了局部扰动频率的概念,基于Hilbert变换求解瞬时频率的方法对畸变信号进行重采样纠正,但频域修正方法具有较多局限性,需要已知声源中的某一个特征频率成分,在特征频率分布比较密集的情况下难以进行有效的带通滤波,而且噪声的存在和滤波器的缺陷造成瞬时频率曲线的波动,从而带来校正误差。
而在时域内进行校正可以有效地避免上述问题,清华大学的杨殿阁[4]等人提出非线性时间映射法,基于声场中的运动学几何关系,建立声源与测量信号之间的非线性时间映射方法,基于运动声源的声源特征函数,在时域消除多普勒效应,取得了较好的结果。
1 多普勒效应
当波源和观察者有相对运动时,观察者接收到的振动频率与波源振动频率不同的现象称为多普勒效应[5]。
在静止的介质中,当波源和观察者的连线与相对速度方向平行时,如图1a所示。观察者接收到的振动频率与波源振动频率可以用式(1)表达;当波源和观察者的连线与相对速度方向相交时,如图1b所示。观察者接收到的振动频率与波源振动频率可以用式(2)表达。

f0为观察者接收到的振动频率;fs为波源的振动频率;C为波在介质中的传播速度;Vo为观察者相对于介质的速度;Vs为波源相对于介质的速度。

图1 多普勒效应
对比式(1)和式(2)可以看出,当波源和观察者的连线与相对速度方向相交时,观察者接收到的振动频率呈现非线性变化。
2 基于瞬时频率的多普勒畸变声信号校正方法
信号频率非平稳性的还原通常使用重采样方法,而建立一组重采样时间序列就是该方法的核心[6]。对于多普勒畸变信号,瞬时频率与原信号频率(假设原信号为单一频率f0信号)存在如下关系:

n为周期内采样点数;fs为原信号采样频率;fsi为畸变信号i点处的采样频率;fi为畸变信号i点处的瞬时频率。采样时间间隔等于采样频率倒数,即dt=1/fs,代入式(3)可得:

dti为重采样时间间隔,因此重采样时间间隔序列可以得出dtrsp=[dt1dt2… dtN-1],从时间间隔可以进一步计算出重采样时间点序列trsp=[0 t1t2… tN-1],重采样时间点序列以畸变信号的起始点为起始点,因此trsp(1)=0,计算公式为:

由于重采样时间点超过畸变信号时间上限时,重采样将失去意义,因此定义重采样时间点序列上限为tM,即trsp=[0 t1t2… tM],其中,M 是不大于N-1的正整数,其值应满足:

多普勒畸变信号的瞬时频率f在任意区间[trsp(i) trsp(i+1)]内是连续变化的,所以采用某时刻的瞬时频率将会带来计算误差,设存在一个较大的整数值K,在时间内可以认为瞬时频率是恒定值[7],则有:
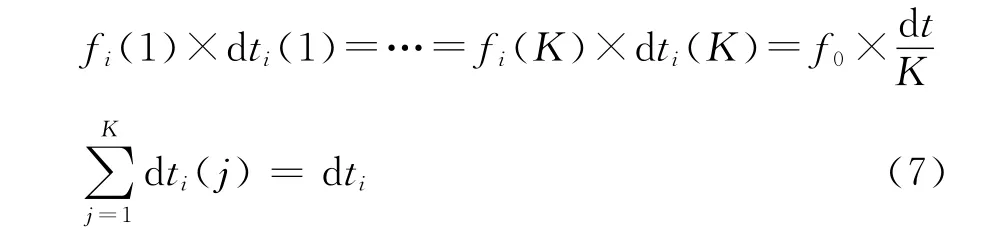
对区间[trsp(i) trsp(i+1)]内的K 个时段求和可得:

当K值足够大时,上式可以用积分表示为:

由trsp(1)=0可进一步得到trsp(i)的表达式为:
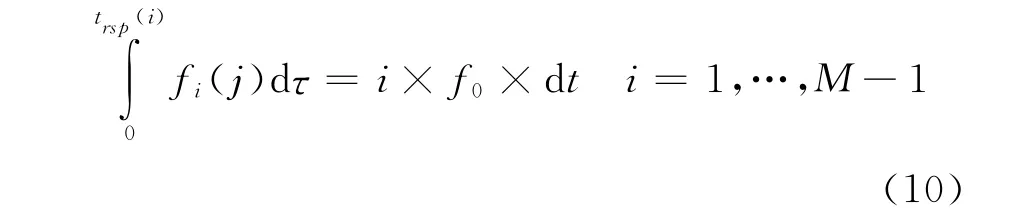
对式(10)进行求解即可得出重采样时间点序列trsp=[0 t1t2… tM],最后通过3次样条函数差值法对多普勒畸变信号x(t)进行重采样,从而得出校正后信号y(t)为:

3 多普勒仿真信号的校正
3.1 仿真信号的建立
在列车速度为亚声速的情况下,考虑列车轴承声源为单极子点声源,并且传播介质为理想流体,即不存在粘滞性,没有能量损耗。建模测量情况的方案如图2所示。根据莫尔斯声学理论,从波动方程和运动关系出发,可以推导出:
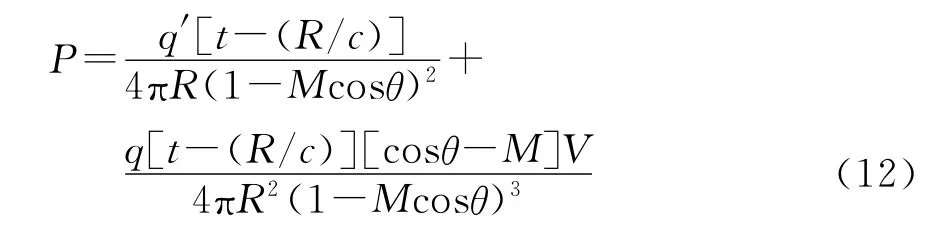
P为麦克风处采集到的声压值;q为单极子点声源的强度;t为运行时刻;R为发声时刻声源与麦克风之间的距离;c为声音在介质中速度;θ为声源与麦克风连线与声源运动方向之间的夹角;V为声源速度;M=V/c为马赫数。式(12)中第2项为小量,可以忽略不计。对于简谐声源q=q0sin(ω0t)有:


图2 建模测量的方案
在上式中,乘积符号左边的部分决定信号的幅值,右边的部分决定信号的相位。对相位进行求导,即可得出频率随时间的变化为:
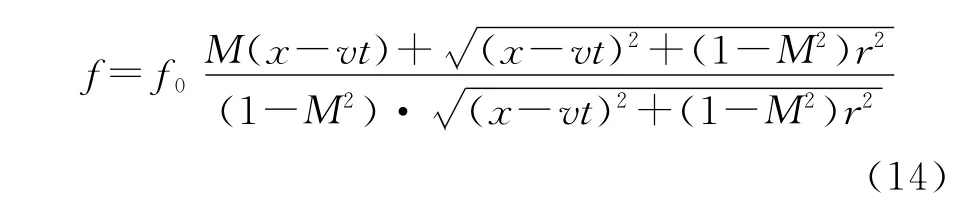
x为采集开始时刻时声源所在位置与麦克风位置的水平距离;r为声源运动轨迹与麦克风的垂直距离。
根据莫尔斯声学理论[8],在此建立一个含有3个频率的信号进行仿真分析,其中设置这3个频率相近(f1=1000Hz,f2=1100Hz,f3=1200Hz),使得不能够简单地通过带通滤波器获得其中任何一个频率变化。给定仿真参数x=5m,r=2m,c=340m/s以及v=20m/s,仿真信号的时域和频率如图3和图4所示。


图4 仿真信号的频率
3.2 仿真信号校正结果
从仿真信号的频谱图可以看出,信号频率分布在800~1400Hz之间。采样频率设定为fs=50 kHz,这也是在后续实验中对列车轴承信号进行声音采集的采样频率。由时频谱中频率分辨率Δf=fs/NFFT可知,给定NFFT的情况下,fs越小,频率分辨率越高。因此,在对信号进行短时傅里叶变换前,首先对信号进行降采样,为保证重采样后的信号仍然包含关键的频率,降采样后的采样率必须满足fs′≥2800Hz,在此选定fs′≥3000Hz。
将校正前和校正后信号的频谱图和视频分布图相比较,如图5所示。可以明显地看出,3个频率均得到了很好的校正,从而验证了方法的有效性。

图5 校正后仿真信号的频谱
4 实验分析
在实验中,声源为一放置在以恒速28.8km/h速度行驶的车辆上的有源音箱,音箱播放f=3000 Hz的声音信号,在实验中取Y=1.5m,S=16m。采集到的信号如图6所示。

图6 实验信号的时域
实验中麦克风选用丹麦B&K公司的声压场麦克风4944-A,采集卡选用美国NI公司的PXI-4472动态信号采集模块,采集箱选用美国NI公司的PXI-1033机箱。
实验信号的频谱如图7a所示。从图7a中可以看出,受多普勒效应影响,在源信号特征频率附近产生了较为明显的频带展宽和频移。校正后的频谱如图7b所示。从图7b中可以看出,频移现象完全消除,频率展宽由原先的4.16%缩小至1%左右,信号得到了较好的校正恢复。

图7 实验信号校正前后信号频谱对比
5 结束语
针对运动声源声音信号的测量中广泛存在多普勒效应干扰问题,从运动关系和莫尔斯声学理论出发,提出了基于瞬时频率的校正方法,从时间序列校正入手对信号进行校正,从仿真信号和实验信号的处理结果来看,多普勒效应带来的特征频率频移和频率扩展的问题得到了有效解决。由于该方法在时域内对采集到的离散信号进行单点计算操作,因此,与以往的频域处理方法相比,具有无需已知声源特征频率的优点,是一种简单、有效的多普勒畸变声音信号校正方法,该方法的使用前提是声源作匀速直线运动,因此,适用于轨边检测系统和声场全息等领域。
[1]Dybala J,Radkowski S.Reduction of Doppler effect for the needs of wayside condition monitoring system of railway vehicles[J].Mechanical Systems and Signal Processing,2013,38(1):125-136.
[2]Stojanovic M,Catipovic J A,Proakis J G.Phase-coherent digital communications for underwater acoustic channels[J].Oceanic Engineering,1994,19(1):100-111.
[3]Johnson M,Freitag L,Stojanovic M.Improved Doppler tracking and correction for underwater acoustic communications[J].IEEE International Conference on A-coustics,Speech,and Signal Processing,1997,(1):575-578.
[4]杨殿阁,罗禹贡,李 兵,等.基于时域多普勒修正的运动声全息识别方法[J].物理学报,2010,59(7):4738-4747.
[5]刘战存.多普勒和多普勒效应的起源[J].物理,2003,32(7):488-491.
[6]张 旻,程家兴,樊甫华,等.利用Hilbert变换提取信号瞬时特征参数的问题研究[J].电讯技术,2003,(4):144-148.
[7]赵义正,杨景曙.基于分数阶Fourier变换的瞬时频率估计方法[J].安徽大学学报,2005,(11):44-49.
[8]P M 莫尔斯,等.理论声学(下册)[M].杨训仁,吕如榆,戴根华,译.北京:科学出版社,1986.

