船体结构应力监测点的选取方法研究

贾连徽，任慧龙，孙树政，李积德，唐浩云

（哈尔滨工程大学 船舶工程学院，哈尔滨150001）

1 引 言

船舶在复杂的海洋环境中航行，由于遭遇恶劣海况、装载不合理或人为操作失误等因素，极易对船体结构造成损伤，而这种由于环境随机因素造成的结构破坏很难通过理论计算进行预测。因此，通过在船体结构中植入应变传感器对结构应力进行实时监测与强度评估是解决这一难题的方法之一。

Nielsen等[1]基于船体结构监测数据对结构的疲劳损伤速率进行了研究；Okasha等[2]通过结构健康监测系统对船体结构性能进行了评估；Wang，Pran等[3]则研究了光纤传感器在船体结构监测中的应用。以上研究中均介绍了监测点的布置位置，但对这些监测点是如何选取的并没有进行说明。船体结构应力实时监测首要解决的问题是监测点的位置选取和传感器的布置方法。由于船体结构庞大而复杂，所受的环境载荷多变，因此对每一构件都进行应力监测几乎是不可能实现的。针对这一问题张岚、侯超等[4-5]以散货船为例，根据中国船级社散货船结构强度直接计算指南，通过舱段结构有限元分析结果，得到散货船舱段部分结构的应力监测部位；金永兴、胡雄等[6-7]则根据集装箱船结构疲劳等事故易发的主要原因、集装箱船的结构特点以及船体结构应力校核部位选取的基本原则，确定了结构应力监测的部位，并通过实船航行试验获取了这些测点处的应力数据；王为等[8]通过对Nishihara箱型梁模型在中垂状态下的应力、应变分布的有限元力学分析，研究水面船舶总纵强度监测时的传感器优化布置原则，并通过改进型粒子群优化算法和混沌算法，以信号覆盖率能满足监测要求为目的，对砰击信号监测的传感器优化配置准则进行了研究，梁文彬[9]等则采用遗传算法对该问题进行了研究。

值得注意的是，以上研究成果大多是建立在对船体结构做了简化和假设的基础上，根据结构应力的大小人为地选取监测点，依赖人的经验，主观影响因素较大，选取结果不具有唯一性；或者仅以信号覆盖率为指标进行传感器的布置研究，而没有考虑船体结构的受力特点。本文在这些研究的基础上，考虑船舶航行区域海况，通过全船有限元分析得到结构的应力响应函数，在此基础上对监测点的选取进行了研究，给出了各部位监测点的选取方法，并通过对监测点的应力状态分析给出传感器的布置形式。

2 求解应力响应函数

本文通过采用MSC.Patran/Nastran进行有限元分析，得到船体结构的应力响应函数。

根据船体结构图采用板（shell）、梁（beam）、杆（rod）及质量（mass）单元建立全船有限元模型。

对全船结构模型施加静水压力、波浪载荷、货物压力、货物惯性力、重力加速度和波浪载荷引起的全船惯性力等，各载荷施加方式见表1。

表1 载荷施加方式Tab.1 Loading mode

静水压力Psw按（1）式计算

式中：ρw为海水密度，g为重力加速度，T为吃水，z为距基线高度。

货物压力Ps按（2）式计算

式中：ρc为货物密度，h为货物顶端高度。

货物惯性力Pd按（3）式计算

式中：ax、ay、az为货物加速度沿三个坐标轴的分量，x0、y0、z0为货物重心点坐标，x、y、z为货物惯性力作用位置。

重力加速度为常数9.81 N/kg，方向沿z轴负方向。

为了能够真实地模拟船舶在波浪上的状态，将船体看作完全自由梁，即在进行有限元求解时对船体结构不施加任何约束条件，而是通过惯性释放的方法进行求解[10]。

通过上述方法即可得到船体结构任意部位的应力响应函数H，H为装载工况、计算频率和浪向等

变量的函数，即

式中：k表示装载工况，ωe表示遭遇频率，β表示遭遇浪向。

3 监测点选择方法

3.1 根据高应力部位选择监测点

将船体结构按其特点分为几类，如甲板与平台、船体外板、舱壁、底纵桁与实肋板、纵向骨材、舷侧肋骨、支柱等七类结构，在每一类结构内将各点应力响应按从大到小排序。

由于全船有限元模型网格单元数量庞大，即使在每一类结构内要将所有的单元应力响应列出也是困难且没有必要的。本文引入参数N，它表示每类结构中所有单元的应力响应按从大到小排序，需要导出进行下一步分析的应力响应最大的前N个单元数量。对参数N的取值，认为当网格尺寸与一个肋位的长度接近时，N取20是合适的。

在有限元分析中，高应力和应力集中部位附近单元应力值均会高于其他部位，因此选出的N个单元应力并不一定代表N个高应力或应力集中部位，多数情况下这些单元分布在几个高应力或应力集中部位附近。为了方便计算机编程找出这些高应力和应力集中位置，规定一个参考距离D，在选出的N个单元中，任意两个单元的距离只要小于D，则保留应力绝对值较大的单元。不妨设选出的N个单元的应力和坐标为

式中：Sn和Cn（xn,yn,zn）分别为第n个单元的应力和中心坐标，且有则任意两单元间的距离为

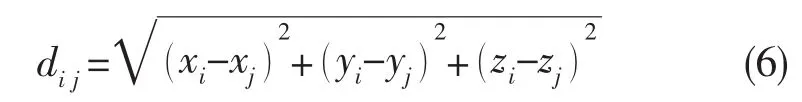
式中：角标i，j表示第i个单元和第j个单元。

计算步骤如下：① 计算d12，若d12＜D则剔除单元2，否则计算d13；② 计算d13，若d13＜D则剔除单元3，否则判断单元2是否被剔除，若存在单元2则计算d23，否则计算d14；③ 以此类推，直至N个单元均计算完毕，流程图如图1所示。

按照上述方法首先对各工况下选出的N个高应力单元进行一次计算，得到各工况下的高应力部位，再将这些部位进行第二次计算，剔除各工况间的重复部位，得到最终的全船高应力部位。

图1 高应力和应力集中位置选取的程序流程图Fig.1 The flow chart for the selection of area of high stress and stress concentration

3.2 考虑海况信息的监测点选择

由上述过程可以看出，选取的位置是各浪向与频率组合的工况中应力响应最大的几个位置，即认为一旦遭遇某一特定海况则通过上述方法选出的位置将是该海况下船体结构最易出现破坏的位置。但是船舶在航行中遭遇某一特定浪向与频率组合的工况的概率是相对较低的，绝大多数情况下船舶是会遭遇各种不同的海况，因此当海况资料完备时，仅由上述方法选取的位置是不够全面的。因此本文通过对各工况下的响应函数进行加权，根据加权平均值来选取结构应力监测点。需要指出的是该方法是在以下两点假设的前提下提出的：（1）船舶的遭遇浪向服从均匀分布；（2）航速对线性波浪载荷的影响不大。

由于船舶的遭遇浪向可近似认为服从均匀分布[11]，因此，相应的权函数仅与船舶的装载工况和遭遇频率有关。对于装载工况的时间分配系数，可根据船舶的实际情况来确定各工况所占的比例，或根据相关规范[12]来确定。对于遭遇频率，可根据船舶航行区域的海浪谱资料求出各遭遇频率的出现概率，将该出现概率与各工况的时间分配系数相乘作为求解加权平均应力响应函数的权值。

船舶的遭遇频率ωe与实际波浪频率ω关系如下：

式中：θ为航向角，U为航速。由于航速对线性波浪载荷影响不大[13]，计算时U可取为定值，即航速的出现概率可取为1，航向角θ的出现概率服从0°～360°之间的均匀分布。因此，在权函数计算时可用实际波浪频率的出现概率代替遭遇频率的出现概率。

设船舶装载工况的时间分配系数为α，波浪频率的出现概率为p，则权函数λ与加权平均应力响应函数为：

式中各符号含义同前所述。

将加权平均应力响应函数作为排序的优先级，再仿照2.1中选取高应力部位监测点的计算方法得到考虑海况信息的监测点。

3.3 权函数的计算

船体结构应力响应函数是在不同的遭遇频率下求得的，根据海浪谱可查得各周期范围内波浪的出现概率。以全球海况[14]为例，根据各周期范围内的波浪出现概率，利用矩形法求得概率密度曲线上各点的数值，如图2中矩形点。对概率密度进行拟合，得到概率密度函数为

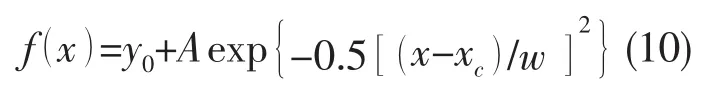
式中各参数拟合值为：y0=0.000 73，xc=8.687 93，w=1.590 47，A=0.247 93。函数曲线如图2中实线。

图2 全球海况周期概率密度函数Fig.2 The curve of probability density-period of global sea states

曲线拟合存在误差是不可避免，因此由（10）式确定的概率密度函数积分值不为1，故需对此函数进行修正。设修正系数为c，则有修正后概率密度函数为

式中修正系数c=1.011 7。

将船舶的遭遇频率转化为周期，利用（11）式即可求得该海况的出现概率，再结合船舶装载工况的时间分配系数，通过（8）式，即可求得相应的权函数。

4 传感器布置方法

通过上述方法即可得到船体结构中对外载荷反应最敏感的部位，即结构监测的布点位置。以下通过对这些敏感部位应力成分的进一步分析来确定传感器的布置方法。

对只受拉压应力作用的杆结构，由虎克定律[15]可知杆内应力为

式中：E为材料弹性模量，ε为应变。而对于一个平面应力状态的结构，通过直角应变花可测得其主应力为

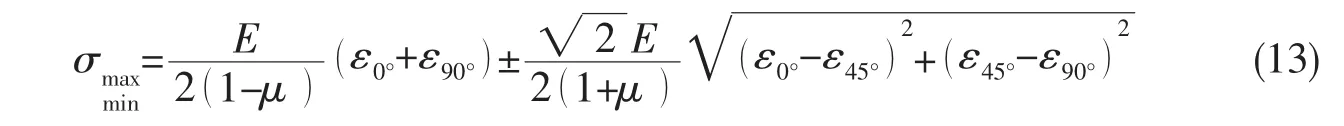
式中：μ 为泊松比，ε0°、ε45°和 ε90°为三个方向的应变，传感器布置方式如图3所示。

对于一个监测点来说，若只受单向拉压应力作用，则可沿受力方向布置一个应变传感器即可，若监测点受力复杂，则需布置三向应变传感器。

利用上文提到的有限元分析方法，可以进一步得到各监测点在不同工况下的受力状态。在选出的监测点部位处建立局部坐标系，使得每一局部坐标的xoy平面在测点所在的结构平面内，对于纵向、横向和垂向构件上的监测点，其x方向分别沿船长方向、船宽方向和垂直方向。

设σx与σy分别为两个垂直方向的应力，则当或时，认为该监测点处两个垂直方向上的受力不在同一量级，可近似看作单向拉压受力状态；当时，认为该监测点可能出现受力复杂的状态，需要布置三向应变传感器。

图3 直角应变花示意图Fig.3 Right angle strain flower

5 算 例

本文应用上述方法对一条补给船进行了结构应力监测点的选取。

该船总长241 m，型宽32 m，型深17.5 m，满载设计吃水10.8 m，有限元模型如图4所示。应力响应计算时，波浪载荷与全船惯性力采用三维线性势流理论计算，船舶装载工况选取满载出港状态，计算波高取单位波幅，频率范围按每0.1 rad/s递增从0.1 rad/s至2.0 rad/s，共计20个频率，浪向范围按每30°递增从0°至330°，共计12个浪向。则总的计算工况个数A=1×20×12=240个。

图4 全船有限元模型Fig.4 Finite element model of the whole ship

以主甲板为例进行说明，主甲板单元共计13 762个，将各工况单元应力按从大到小排序，提出前20个单元的坐标。表2中列出了ω=1.0，β=0°时各单元的坐标信息。按照3.1节中所述方法，选取距离取船宽的八分之一，即D=4 m，经一次筛选计算后得到该工况下应力集中部位最大应力单元ID号为：11610032、11665343、16722、48831、64968、256、11665356、11610045和84983。

将240个工况均按上述步骤进行筛选，再将选出的单元进行第二次筛选计算，并记录此次筛选过程中各单元的出现次数，按这一出现次数进行优先级排序，当有两个单元的出现次数相同时，按各单元的最大应力大小排序，筛选结果见表3。

通过对筛选结果的观察发现，所选取的监测点均位于甲板开口角隅及其附近位置，且与迎浪状态下选取结果一致。

表2 按应力排序的单元坐标信息Tab.2 Unit coordinates information sorted by stress

表3 根据高应力部位选取的监测点Tab.3 Monitoring points selected by area of high stress

以上方法是根据高应力部位选择监测点，在没有确定船舶航行的海域或没有海况资料时，通过上述方法可以确定船体结构中最适合进行应力监测的部位。

上述算例中的实船的航行海域为全球海域，根据应力响应函数计算所选取的频率，将其转化为相应的周期代入（11）式得到各计算工况的出现概率，见表4。

表4 船舶遭遇不同周期波浪的出现概率Tab.4 The probability of encountering wave with different periods

续表4

若只考虑船舶满载工况，即认为α=1，则表4中的出现概率即为按（8）式求得的权函数大小。将此权函数和上面求得的应力响应函数代入（9）式求出加权平均应力响应，并按此排序，再按前述筛选的计算方法进行筛选，得到考虑海况信息选取的监测点，见表5

表5 按加权平均应力排序的单元坐标信息Tab.5 Unit coordinate information sorted by weighted mean value of stress

表6中列出了舷侧、底纵桁、横舱壁位置处两种方法选出的前三个监测点（舷侧部位仅选出两个），比较表3、表5和表6可以看出，两种方法选出的监测点基本一致，且包含规范[16]中提及的危险部位，证明了方法的可行性，同时说明在没有海况信息时根据高应力部位选择监测点的方法也是较为可靠的，表6中最后一列给出了仅由迎浪状态按考虑海况信息选取的监测点，可以看出其结果与各浪向加权结果一致。

表6 两种方法选出的监测点Tab.6 Monitoring points selected in the two methods

表7中列出了部分监测点x方向和y方向最大应力及其比值，并给出了按前文所述方法确定的该部位传感器的布置形式。其中单元ID号为11665356、16722的单元位于甲板舱口角隅，256号位于甲板纵骨，从表中的布置形式可以看出舱口角隅处的受力较为复杂，需要布置三向传感器，而甲板纵骨主要以拉压应力为主，可以布置沿其主要受力方向的单项传感器；舷侧、横舱壁以单项受力为主，底纵桁受力则较为复杂。

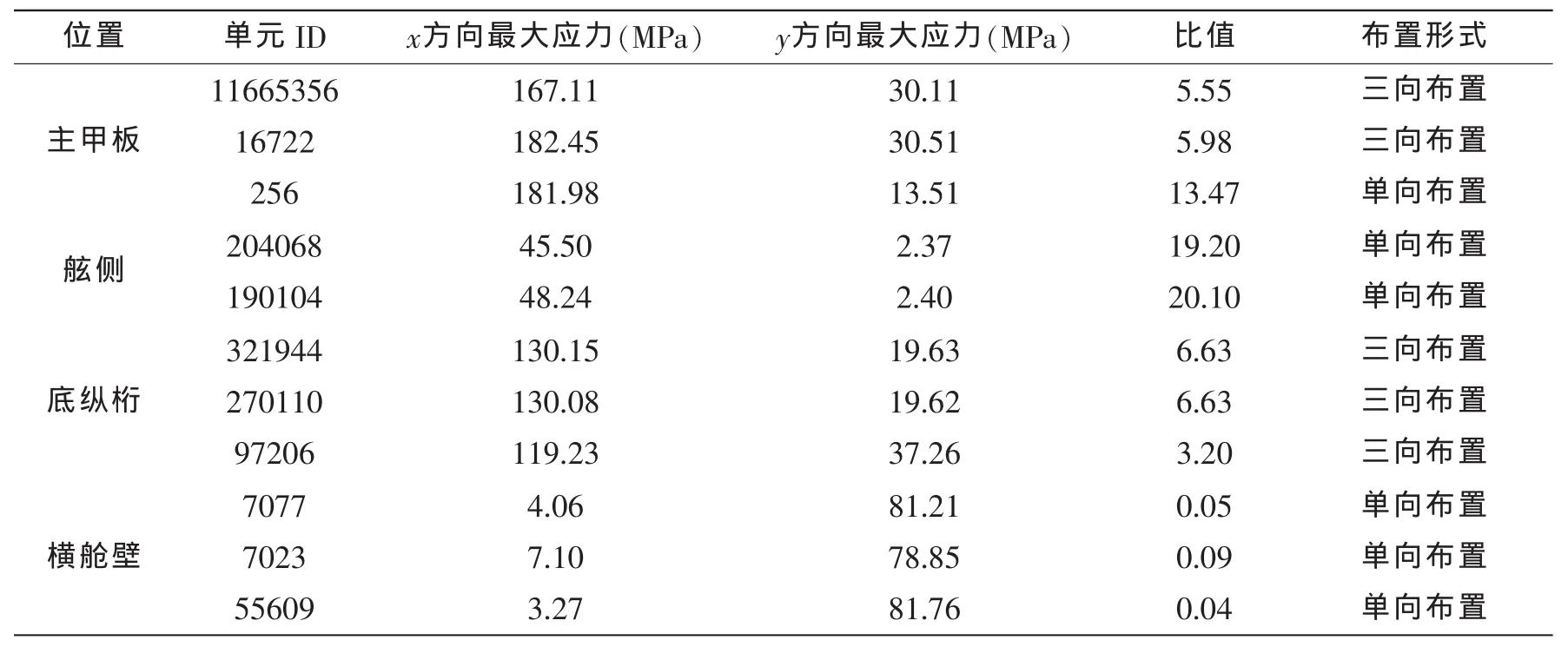
表7 监测点传感器布置形式Tab.7 Sensor arrangement of monitoring points

6 结 论

本文在求得船体结构应力响应的基础上，建立了根据高应力部位和考虑海况信息两种途径对船体结构应力监测点进行选取的方法。根据高应力部位选择监测点的方法适用于船舶的航行区域不确定时或缺乏海况资料的情况；当船舶的航行海区明确并具有完备的海况资料时，利用考虑海况信息进行监测点选择的方法是更加合理的。

通过应用本文所述的方法对实船的算例分析得到如下结论：

（1）本文所述方法选出的监测点包含规范中涉及的由于易损而需进行结构加强的部位；

（2）根据高应力部位选取的监测点与考虑海况信息选取的监测点位置在优先级较高时基本一致；

（3）仅考虑迎浪状态选取的监测点与考虑各浪向选取的监测点在优先级较高时基本一致；

（4）船舶甲板舱口角隅和底纵桁是受力较为复杂的部位，需要布置三向传感器，而甲板纵骨、舷侧和横舱壁结构受力相对简单，可以布置单向传感器。

[1]Nielsen U D,Jensen J J,Pedersen P T,Ito Yuichi.Onboard monitoring of fatigue damage rates in the hull girder[J].Marine Structures,2011,24:182-206.

[2]Okasha N M,Frangopol D M,Decò A.Integration of structural health monitoring in life-cycle performance assessment of ship structures under uncertainty[J].Marine Structures,2010,23:303-321.

[3]Wang G,Pran K,Sagvolden G,Havsgard G B,Jensen A E,Johnson G A,Vohra S T.Ship hull structure monitoring using fibre optic sensors[J].Smart Materials and Structures,2001,10:472-478.

[4]张 岚.基于FBG技术的散货船结构监测传感器布置研究[D].武汉:武汉理工大学,2008.Zhang Lan.Research on the arrangement of bulk carrier structure monitoring sensor based on FBG technology[D].Wuhan:Wuhan University of Technology,2008.

[5]侯 超.船体强度状态监测技术研究[D].武汉:武汉理工大学,2008.Hou Chao.Monitor technology research on hull strength state[D].Wuhan:Wuhan University of Technology,2008.

[6]金永兴,胡 雄,施朝健.集装箱船舶结构状态监测与评估系统[J].上海海事大学学报,2008,29(3):1-4.Jin Yongxing,Hu Xiong,Shi Chaojian.Supervision and evaluation system of container vessel hull structure[J].Journal of Shanghai Maritime University,2008,29(3):1-4.

[7]胡 雄,孙德建,金永兴,续秀忠.集装箱船舶结构状态的在线监测技术研究[J].中国工程机械学报,2009,7(4):459-462.Hu Xiong,Sun Dejian,Jin Yongxing,Xu Xiuzhong.Online monitoring technologies for container ship structures[J].Chinese Journal of Construction Machinery,2009,7(4):459-462.

[8]王 为,林玉池,沈小燕,赵美蓉,宋 乐.基于自适应粒子群算法的光纤光栅传感器优化配置[J].天津大学学报,2010,43(10):890-894.Wang Wei,Lin Yuchi,Shen Xiaoyan,Zhao Meirong,Song Le.Optimal placement of fiber bragg grating sensors using self-adaptive particle swarm optimization algorithm[J].Journal of Tianjin University,2010,43(10):890-894.

[9]梁文彬.基于光纤光栅的船舶结构健康监测技术研究[D].天津:天津大学,2011.Liang Wenbin.Study on ship hull structural health monitoring technology based on fiber bragg grating[D].Tianjin:Tianjin University,2011.

[10]张少雄,杨永谦.船体结构强度直接计算中惯性释放的应用[J].中国舰船研究,2006,1(1):58-61.Zhang Shaoxiong,Yang Yongqian.Application of inertia relief in direct calculation of structural strength for ships[J].Chinese Journal of Ship Research,2006,1(01):58-61.

[11]杨代盛,桑国光,李维扬,戴仰山.船舶强度的概率方法[M].哈尔滨:哈尔滨工程大学出版社,2007.

[12]中国船级社.船体结构疲劳强度指南[M].北京:人民交通出版社,2005.

[13]戴仰山,沈进威,宋竞正.船舶波浪载荷[M].北京:国防工业出版社,2007.

[14]IACS Recommendation No.34 Standard Wave Data[S].2000.

[15]欧贵宝,朱加铭.材料力学[M].哈尔滨:哈尔滨工程大学出版社,2008.

[16]中国船级社.钢质海船入级与建造规范[M].2006.