半潜平台波浪载荷不确定性及结构疲劳可靠性研究

杨 鹏，顾学康

（中国船舶科学研究中心，江苏 无锡214082）

1 引 言

由于海洋平台结构制造工艺、材料属性、强度和载荷计算中的一些假设等，传统的确定性强度评估方法在海洋结构物的安全性设计校核中存在一定缺陷，更为合理的结构强度和载荷评估手段必须基于概率学理论以保障海洋结构物具有足够的安全可靠性，因此，先进的海洋结构物设计规范均要求对海洋平台结构进行可靠性设计。在疲劳载荷计算过程中，由于在对海况的描述、波浪力的计算、结构的应力分析等方面采用了种种假设和理想化模型，因此，计算所得的应力范围与真实的应力范围之间存在着误差。Guedes Soares[1]主要针对北大西洋海况和全球海况详细分析了波浪载荷短期响应和长期响应中的各种不确定性因素，但是作者没有针对西北太平洋海域进行分析，而此海域对中国的船舶和海洋工程设计尤为重要。另外，Guedes Soares主要分析的是船舶总体波浪载荷短期和长期预报的不确定性，并没有给出疲劳寿命计算中所需要的疲劳载荷短期和长期响应的不确定性分析。Moan等人[2]使用北大西洋29年的海况统计资料分析了1、2、4、29年四种情况下由海况资料变化引起的有义波高HS统计值随海况资料统计年数的变化规律。同时分析了北大西洋海况统计资料年度变化对长期波浪载荷的影响，并对FPSO的垂向弯矩、半潜平台的结构局部应力及疲劳载荷进行了不确定性分析。吴东伟[3]和杨鹏等[4]针对半潜式平台的短期和长期波浪载荷预报中的不确定性进行了分析，其中考虑了谱型的不确定性、波高的不确定性和载荷传递函数的不确定性。

为了研究半潜平台疲劳寿命计算中波浪载荷的不确定性和结构的疲劳可靠性，需要建立随机波浪载荷作用下考虑不确定性因素影响后的结构疲劳寿命评估表达式。在评估波浪载荷传递函数的不确定性时利用了波浪载荷模型试验结果。对于波高和平均跨零周期的不确定性，本文基于方钟圣等[5]统计的西北太平洋波高和平均跨零周期的器测和目测海况资料，详细研究了不同海况下的波高和周期的回归修正公式以及波浪周期不确定性对结构应力幅值和疲劳寿命的影响。之后利用中国南海S4区的长期海况散布图研究了海况发生概率不确定性对结构疲劳寿命的影响，同时利用该区的浪向分布规律研究了浪向的不确定性及其对结构疲劳寿命的影响。最后根据波浪载荷不确定性以及结构疲劳分析中的其他不确定因素计算了半潜平台典型结构的疲劳可靠度。

2 疲劳寿命分析中的不确定性因素

对于特定海区作业的海洋平台，其服役期间所遭遇海况的长期统计特性可由该海区的波浪散布图确定。根据疲劳损伤线性累积法则，总的疲劳应力参数可由各短期海况的疲劳应力参数线性叠加而得。考虑雨流修正和低应力范围修正后，当应力短期分布服从Rayleigh分布时，结构疲劳应力参数可表达为[6]：

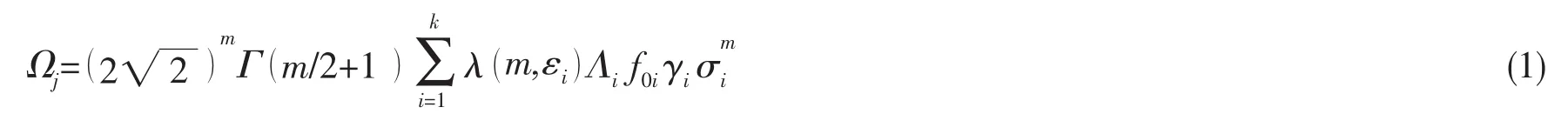
式中：Ωj为某一浪向下的应力参数。根据ABS（2003）[7]规范，总的疲劳应力参数：

其中：q为总的浪向数，pj为各浪向出现概率，σi为第i海况中交变应力幅值标准差，Γ为伽马函数，f0i表示各个短期海况的应力响应跨零频率，γi表示各个HS和TZ组合（短期海况）出现的概率，k表示波浪散布图中短期海况总数，εi为带宽系数，λ（m,εi）表示雨流修正系数[8]，Λi为考虑低应力范围的疲劳损伤修正系数[6]。将公式（1）代入公式（2）中，得到总的疲劳应力参数为：

计及疲劳累积损伤度和应力参数的不确定性，S-N曲线方法中结构的疲劳寿命为：

式中：A为S-N曲线参数的随机变量；△为考虑疲劳累积损伤度的随机变量；疲劳载荷计算中的不确定性因素则通过随机变量B来计及。应力参数Ω仍根据应力范围的计算结果S来计算，作为确定值处理。由于疲劳载荷效应计算中的不确定性B是包含在应力参数Ω中的，因此要探讨B的不确定性需要从应力参数Ω的表达式出发。由于疲劳载荷计算是一个复杂的过程，因此疲劳载荷计算中的不确定性来源有很多。为了便于将不确定性量化，实际中还常把它分解成几个部分给予考虑。以海洋平台中管节点的热点应力范围的计算为例，Wirsching等认为可从以下五个方面考虑不确定性，即：结构的制造和安装方面；对海洋波浪的描述方面；作用在结构上的波浪力的计算方面；结构内名义应力的计算方面；热点应力集中系数的计算方面，以下将主要分析和研究与波浪载荷有关的不确定性。

3 波浪载荷的不确定性分析

结构疲劳寿命可靠性分析中波浪载荷的不确定性来源主要有：（1）海况发生概率的不确定性；（2）波浪谱型的不确定性；（3）有义波高与跨零周期的不确定性；（4）浪向出现概率的不确定性；（5）载荷传递函数的不确定性，等等。计入不确定性因素影响后公式（3）变为：

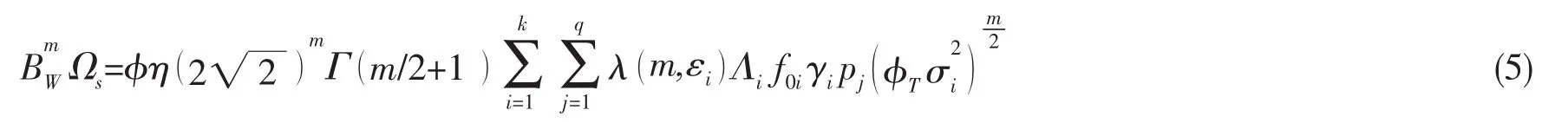
式中：Ωs为不计及不确定因素的标准应力参数；假设与波浪载荷不确定性有关的统计参数BW服从对数正态分布，根据概率学知识可知也服从对数正态分布，为与应力参数不确定性有关的偏差系数；φ为海况发生概率的不确定性引起的偏差系数；η为浪向的不确定性引起的偏差系数；φT（α,Hs,Tz）为综合考虑了谱型、波浪载荷传递函数、波高和平均跨零周期的不确定性影响后各短期应力幅值响应谱的方差的总偏差系数，即应力幅值响应谱的0阶矩（即）的偏差系数，其可以表示为：

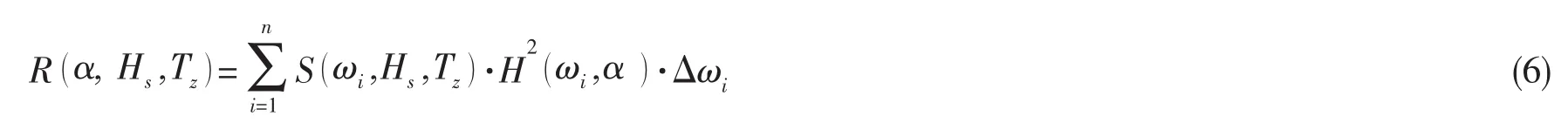
式中：S（ωi,Hs,Tz）为海浪谱，H（ωi,α）为浪向 α 度时的应力幅值传递函数。

3.1 海浪谱型的不确定性

谱型不确定性可简单理解为对于一个短期海况（Hs,Tz），如果采用不同海浪谱来描述，那么相应计算结果是不同的。由于计算中采用的海浪谱一般为理论的谱型公式，与实际海浪情况会存在差别，从而引入了一系列的不确定性因素。目前工程界推荐的海浪谱有P-M谱，JONSWAP谱，双峰谱等等。

平台波浪载荷均方响应（mean square response）即响应谱的0阶矩，可以表示为：

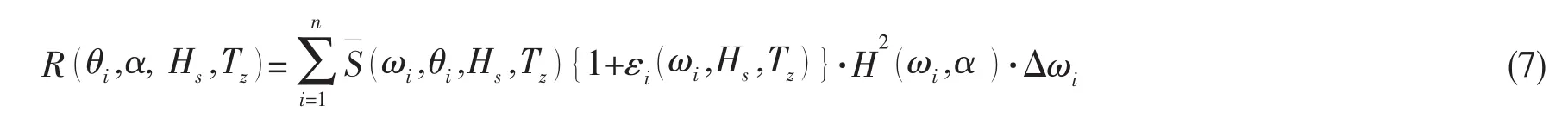
式中：H（ωi,α）为浪向α度时的平台载荷响应传递函数，θi表示不同的谱型，εi为零均值正态分布的随机变量。

载荷均方响应R也是正态分布的随机变量，其均值和变异系数为：

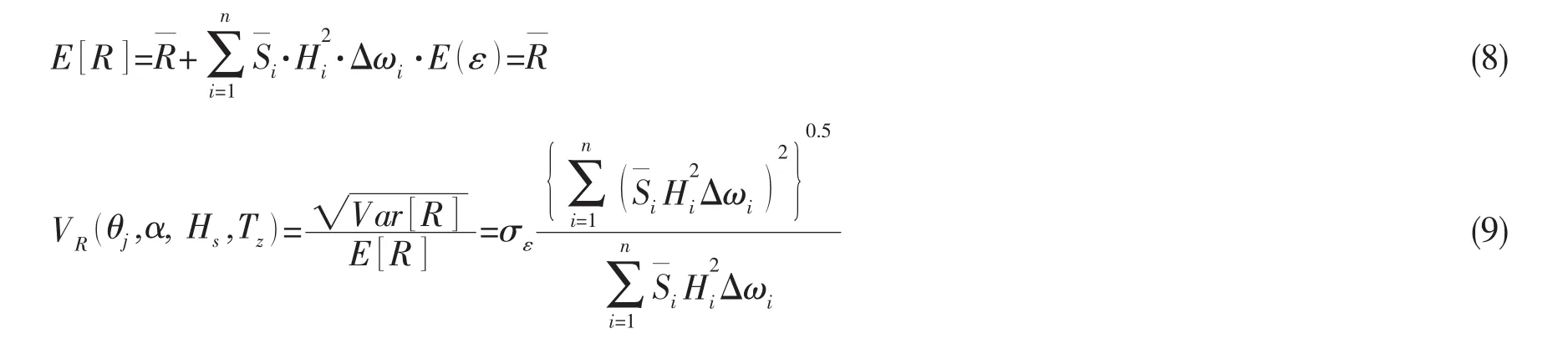
Haver等[9]通过对船舶载荷响应计算和分析指出，当谱间隔为0.01 Hz时，均方差σε的值可取为0.5～0.55。如果为了更好地描述波谱而选择较小的谱频率间隔，那么应该适当增大σε值。

以上是采用一个谱型来描述一个浪向下的载荷响应时产生的不确定性，给出了均方响应的均值和方差的表达式。因谱型的不同而产生的不确定性可以用多个载荷响应谱的0阶矩加权来描述，每个谱型将对应一个条件概率，那么总的均值和方差为：

式中：θ表示不同谱型，fθ表示不同谱型出现概率，可见R的不确定性来自于谱型本身的不确定性和谱型之间的差别。采用标准谱型的载荷均方响应值可以用如下方法确定：

其中：S（ω）可选择ISSC双参数谱（即P-M谱），H（ω）取数值计算所得的传递函数。

于是相对于标准谱方法的偏差系数（Bias）表示为：

这里φS与R分布形式相同，也是正态分布变量，该偏差系数均值和变异系数为：

本文选择P-M和JONSWAP谱来综合模拟实际海浪，分析波谱表达式对谱型不确定性的影响。根据Guedes Soares[1]的分析结果，北大西洋海况中P-M谱的发生概率为：p（HS）=0.86-0.06HS，HS≤14.33 m；p（HS）=0，HS＞14.33 m。σε值取0.525，JONSWAP谱的谱峰提升因子取3.3，将标准谱设定为P-M谱。列出半潜平台生存工况下（HS=13.7 m，TZ=11.89 s）三种主要总体载荷[10]不确定性分析结果，如表1。

从表1可以发现生存工况下谱型偏差系数的均值在0.90～0.99之间，COV在0.17～0.19之间。可见谱型偏差系数的均值接近于1，而COV较大，说明谱型不确定性主要引起较大的离散性。

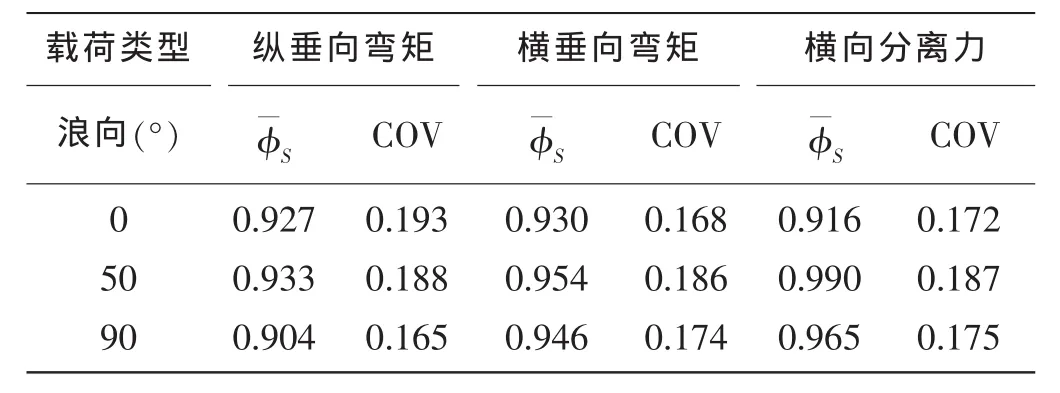
表1 谱型偏差系数的均值和变异系数Tab.1 Mean value and COV for spectrum bias

3.2 波高的不确定性

Guedes Soares[1]在前人的观测数据和理论分析的基础上，经过细致总结，给出了北大西洋真实有义波高值HS和观测值HV之间的回归方程：

式中：HV一般从海况资料中选取；ε为服从零均值正态分布的随机变量，其标准差为s。

那么波高偏差系数的均值和变异系数为：

根据公式（6）可知波浪载荷均方响应与波高的二次方成正比，那么由波高不确定性导致的波浪载荷均方响应的偏差系数均值为：

根据公式（17）和（18）计算波高偏差系数的均值和COV，得到表2结果。

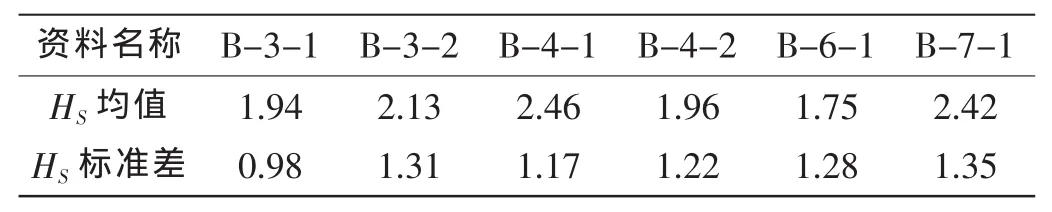
表3 浮标测量结果（HS）Tab.3 Measurement results of buoy

表4 船舶观测结果（HV）Tab.4 Visual results of ship

表5 ε的标准差Tab.5 Mean variance of ε

本文根据方钟圣等[5]统计的西北太平洋有义波高海况资料（见表3和4），使用HS和HV均值拟合出HS和HV之间的关系式：

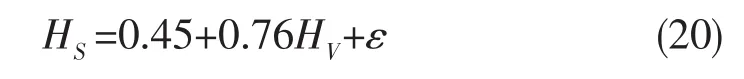
式中：ε为服从零均值正态分布的随机变量，其标准差为s待定。

由概率论可知HS和HV的方差关系为：

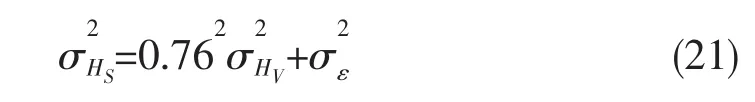
由表3和表4中的HS和HV的标准差可以得到 σε，见表5。

表6 西北太平洋计算结果Tab.6 Results in Northwest Pacific

从表2和表6的比较可以看出，本文总结的波高公式比Guedes Soares公式计算的COV小。可能原因在于本文计算公式回归的是西北太平洋的波高统计资料，而Guedes Soares回归统计的是北大西洋的海况资料，后者的海况偏于恶劣，统计离散性和各有义波高下标准差较大。

3.3 平均跨零周期的不确定性及其对应力幅值的影响

平均跨零周期的器测值和船舶报目测值之间存在一定差别。Guedes Soares[1]针对Famita（1976/1977）的海况资料中的周期数据，线性拟合结果如下：

式中：Tm为器测平均过零周期，Tv为目测周期，其相关性系数为0.75。

本文对西北太平洋器测平均跨零周期和船舶报之间的关系进行了分析，可为在该海域作业的船舶与海洋工程的设计提供参考资料。方钟圣等[5]统计的西北太平洋的波浪平均跨零周期海况资料见表7和8。

表7 浮标测量的周期Tab.7 Measured period by buoy

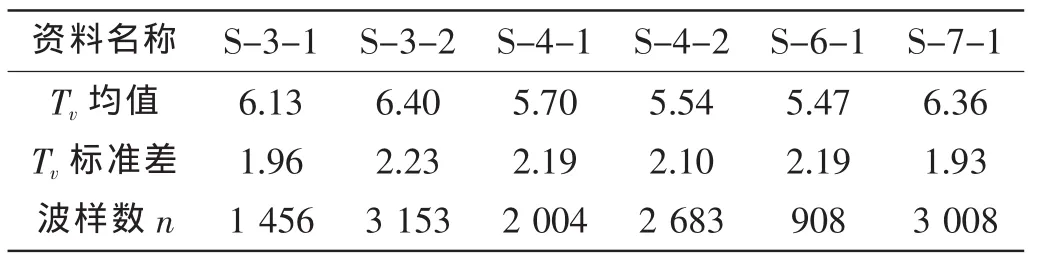
表8 船舶观测的周期Tab.8 Visual period by ship

器测平均过零周期和目测周期之间的修正回归公式如下：

式中：A和B均为与海况资料有关的常数；ε为服从零均值正态分布的随机变量，其标准差为σε；此处假设每个周期Tv处有足够的测量样本点。那么平均过零周期偏差系数φp的均值和变异系数Vp为：

针对表7和8进行线性回归拟合，得到结果如下：

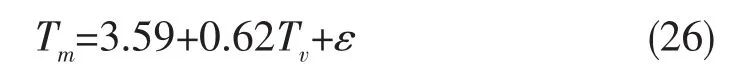
由概率论可知Tm和Tv的方差关系为：

表9 ε的标准差Tab.9 Standard variance of ε

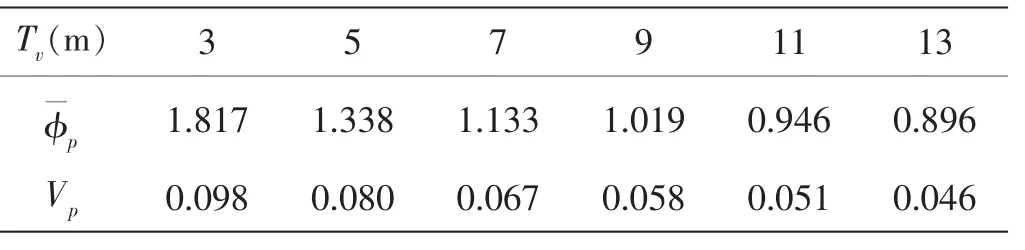
表10 西北太平洋计算结果Tab.10 Result in Northwest Pacific

考虑平均跨零周期不确定性的影响后，应力幅值响应谱的0阶矩可以表示为：

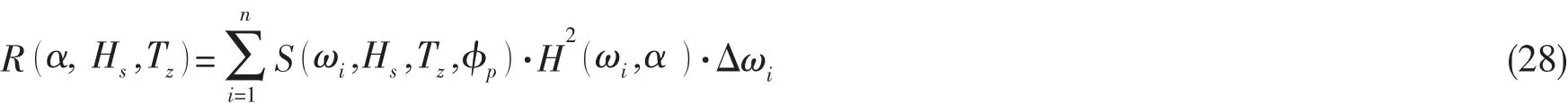
当φp=1.0时，根据公式（28）可以得到无偏的当时，仅考虑平均跨零周期不确定性的影响后R的均值为那么由平均跨零周期不确定性引起R的偏差系数φz的均值为：

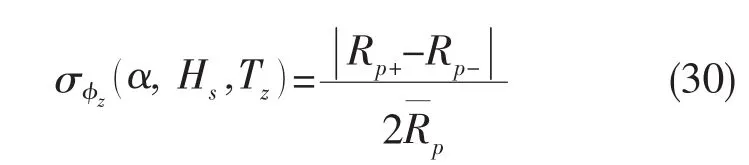
可以通过Taylor展开证明公式（29）和（30）具有一阶精度。那么φz的变异系数Vz为：

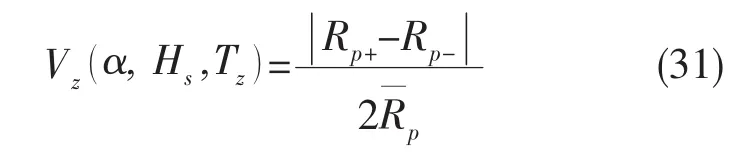
从公式（29）和（30）中可以看出φz的均值和COV均与有义波高无关，本文针对半潜平台计算得到φz的均值和COV见表11。

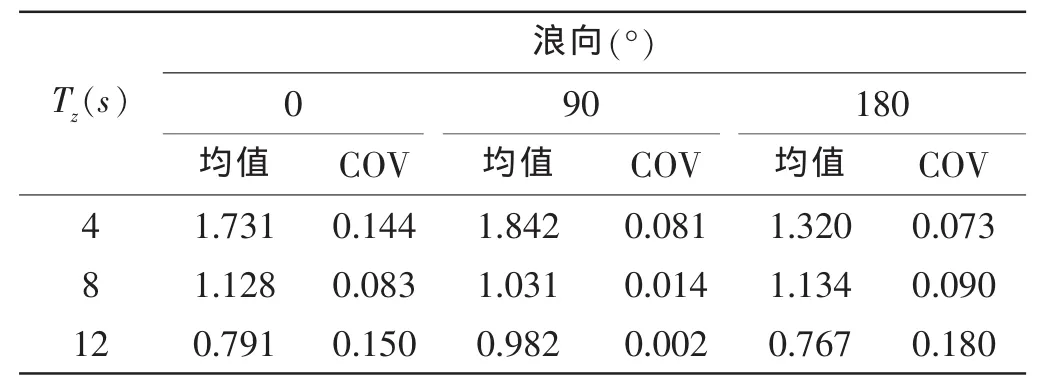
表11 φz的均值和COVTab.11 Mean and COV of φz

3.4 波浪载荷传递函数的不确定性

为了合理考察半潜平台波浪载荷传递函数的不确定性，需要开展半潜平台波浪载荷模型试验研究。某半潜平台的波浪载荷模型试验在CSSRC 05耐波性水池进行，模型缩尺比1:40。本文的波浪载荷试验测量的是中纵剖面的横垂向弯矩和水平分离力载荷传递函数，同时将试验值作为真实值，其中试验中各种因素引起的变异系数为5%。

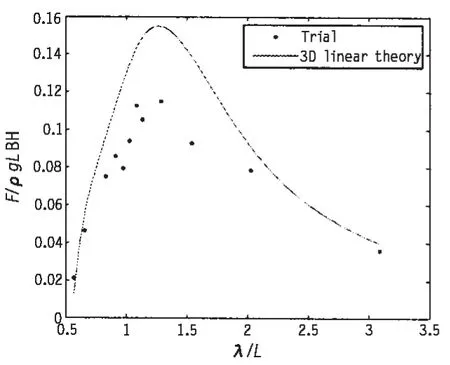
图1 水平分离力Fig.1 Horizontal splitting force

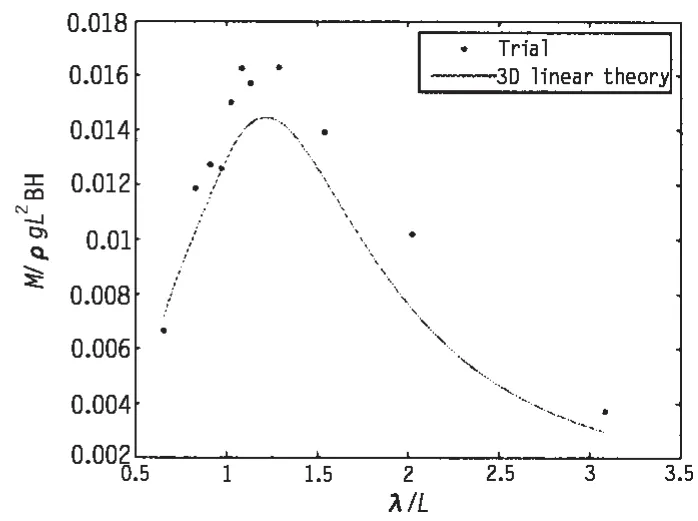
图2 横垂向弯矩Fig.2 Transverse vertical moment

峰频区域附近90°浪向下横垂向弯矩和水平分离力传递函数的数值计算结果（SESAM）和模型试验结果如图1和2所示，可以发现，横垂向弯矩和水平分离力的试验结果和数值结果比较吻合，下面针对横垂向弯矩和水平分离力的传递函数进行不确定性分析。以试验结果作为真实值，理论预报计算值作为理论值来估计偏差系数的均值和变异系数，结果如表12。由于在试验过程中，测量系统存在一定的系统误差和偶然误差，同时横垂向弯矩引起的结构应力会远大于水平分离力引起的结构应力。这样水平分离力的测量信号会较小，其测量误差很可能是大于横垂向弯矩的，表12中水平分离力COV大于横垂向弯矩的COV证实了这一点。

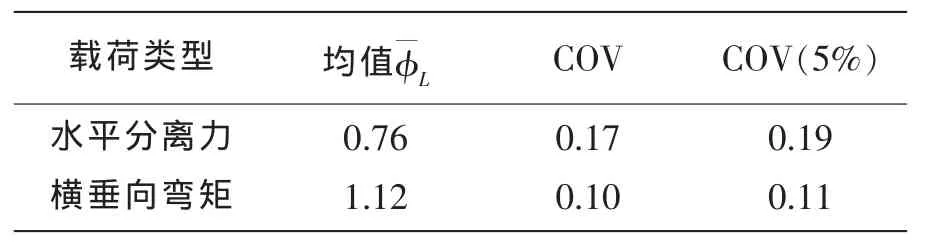
表12 载荷传递函数偏差系数的均值和变异系数Tab.12 Mean and COV for uncertainty of load transfer function bias

考虑试验中5%的不确定性后，横垂向弯矩传递函数的COV为，水平分离力传递函数的COV为以表12中横垂向弯矩和水平分离力传递函数的偏差系数的均值和COV为参考，有理由假设波浪载荷传递函数的偏差系数BF均值在0.76～1.14之间，偏差系数COV在0.11～0.19之间。本文波浪载荷传递函数的偏差系数均值和COV分别取0.90和0.15，并将这些数据推广到各个浪向。同时根据公式（6）可知应力均方响应与载荷传递函数的平方成正比。

3.5 海况发生概率的不确定性及其对应力参数的影响

一般来说，海况资料来自于对多年海况数据的统计归纳分析，由于海况资料随季节和年度具有时变性，对不同时期海况数据进行统计而得到的海况资料存在较大差别，同时使用不同年限的海况资料对疲劳寿命评估影响也很大。一般来说结构的设计疲劳寿命是几十年，如果海况资料的统计年限少于疲劳设计寿命，那么疲劳寿命评估结果必然存在较大的误差，因此一般统计资料中的海况发生概率需要进行适当的修正后才能得到设计寿命期海洋结构物所经历的合理海况。Moan等[2]使用北大西洋1年、2年、4年和29年不同统计周期的海况资料对长期极值预报和疲劳寿命评估的影响进行了研究。以1年为统计周期的海况资料可以得到29个疲劳损伤值，对FPSO来说疲劳损伤最大值和最小值的比值为4.3，对半潜式平台为1.9，可见不同统计周期的海况发生概率对疲劳寿命评估结果影响较大。Nolte[11]的研究表明有义波高随年度的变化很大，另外Guedes Soares和Ferreira[12]对海况年度变化性进行了分析。

为研究海况散布图中海况发生概率的不确定性，采用P-M谱描述海浪谱，使用方钟圣等[5]提供的中国南海S4海区的海况资料来评估半潜平台结构的疲劳寿命。S4区的海况资料分春夏秋冬和全年，同时浪向均分为八个浪向和“所有浪向”，S4区共有45张海况散布图。

表13 疲劳寿命Tab.13 Fatigue lives

假设各浪向出现概率均等，分别使用S4区中四个季节的和全年的包含所有浪向的海况散布图（共五张散布图）来计算结构疲劳寿命，得到的结果见表13。其中“四季加权和”指根据春夏秋冬四个季节的应力参数计算结果加权和后计算得到的疲劳寿命。可见根据不同季节海况散布图计算的结构疲劳寿命存在很大的波动性，以四季加权和的结果为基准进行无量纲化，四个季节疲劳寿命计算结果的波动如表13。疲劳寿命最大值和最小值的比值为4.3，分别发生在夏季和秋季，而且可以看出秋冬季节比春夏季节海况更恶劣。从表13中还可以发现四季加权和与全年海况散布图的计算结果不一致，四季和结果为全年的1.05倍，造成这种差别的原因在于四个季节的海况资料散布图加权和与"全年海况散布图"是存在一定差别的，以及先分季节计算各应力参数然后累积应力参数结果来计算疲劳寿命与先加和各季节散布图然后计算疲劳寿命在方法上的差别。例如在包含所有浪向的海况散布图中，考虑有义波高在0～0.5 m之间，平均跨零周期为6 s的短期海况发生概率，四个季节的加权和为23.75，而“全年海况散布图”中为29，可见差别是明显的。按照Miner疲劳累积损伤的原则，现实海况造成的疲劳损伤应该是通过计算四个季节分别造成的疲劳累积损伤，然后累计出总的疲劳损伤。如果直接使用“全年海况散布图”，将与上述计算结果存在一定的偏差，这在表13中已经体现出来。因此，下文将考虑海况发生概率的不确定性对应力参数Ω的影响。

从另外一个角度，假设各浪向出现概率均等，当考虑海况发生概率的不确定性对应力参数的影响时，真实应力参数可以表示为：

式中：Ωs为无偏的应力参数名义值，k为短期海况数，q为浪向数；φ为偏差系数随机变量，用来表示海况发生概率的不确定性；n代表四个季节。

采用包含“所有浪向”的全年海况散布图计算的应力参数为名义值Ωs，而以相应四个季节海况散布图的联合作用计算的应力参数为真实值来研究偏差系数φ，四个季节应力参数的加权和与全年比值为φ。采用公式（32），根据每个季节海况散布图而计算得到的应力参数与“全年海况散布图”的计算结果的比值见表14。从表中可见海况发生概率不确定性对疲劳应力参数的影响较小。

表14 偏差系数Tab.14 Bias

3.6 浪向的不确定性及其对应力参数的影响

现实中海洋平台或船舶的艏部朝向均有一定的随机性，而海况现实中浪向一般也都不是均匀分布，这样迎浪角的确定工作有很大难度，只能使用随机变量通过统计学规律进行研究。实际工程设计中的波浪载荷评估一般假设迎浪角是均匀分布的，这个假设是基于一些统计数据，而且迎浪角的均匀性假设方便计算。针对西北太平洋的S4区块，本文使用该区全年海况统计资料对浪向的不确定性进行研究，考虑浪向的不确定性对疲劳寿命评估的影响。从S4区全年海况散布图[5]中可以看出不同浪向下海况散布图是不一样的，可见海况散布图较复杂。

（1）浪向发生概率的不确定性

本文为了研究半潜平台的艏部朝向对结构疲劳寿命评估的影响，先假设半潜平台的艏部朝向在服务寿命期间不变，这样可以通过海况资料中的浪向分布规律，得到平台迎浪角的分布规律。同时海况资料选用全年资料中包含所有浪向的那张海况散布图。将艏部朝向分为四种情况：正东、正南、正西和正北，文献中S4区海况资料的0°浪向约定为正北，根据公式（4）（B=1）计算得到的疲劳寿命结果见表15，表中“均匀浪向角”的计算结果指浪向的分布是均匀时的疲劳寿命，也即根据“东”、“南”、“西”、“北”四个艏部朝向时的应力参数的加权和计算的疲劳寿命。从表15中可以发现不同艏部朝向得到的疲劳寿命结果相差很大，其中朝南最为安全，因此在该海域作业时平台艏部应朝南为好。当平台艏部各个朝向的概率一样时，那么迎浪角的分布相当于是均匀的，此时得到的疲劳寿命即“均匀浪向角”结果。由于浪向随季节和年度具有很大的变化性，海况资料中统计的浪向数据必然有较大的不确定性。加上船舶或海洋平台艏部朝向的随机性，影响结构疲劳寿命的迎浪角的分布也有待研究，这需要实际使用中的统计数据支持才能进行相关分析。

为了研究浪向出现概率对应力参数Ω的影响，本文选用S4区全年统计海况资料中包含所有浪向的那张海况散布图，应力参数的计算式采用公式（3）。令均匀迎浪角分布下计算的应力参数Ω为标准应力参数Ωs，真实迎浪角分布下计算的应力参数为ΩD。此种应力参数偏差系数定义为η1，计算表达式见（33），其计算结果为0.824。本次计算中真实迎浪角分布规律采用S4区全年统计海况资料中各浪向出现概率的分布规律，根据S4区海况资料浪向的方位约定，这相当于以正南为平台艏部朝向，浪向分布规律见表16。

表15 艏部不同朝向时的疲劳寿命Tab.15 Fatigue lives with different headings

表16 浪向分布规律Tab.16 Distribution rules of wave direction

（2）不同浪向海况资料的不确定性

在S4区块的全年统计海况资料中，不同浪向的海况资料与包含所有浪向的海况资料是有区别的。一般疲劳寿命评估中使用的海况资料是包含所有浪向的海况资料，而更为真实的结构疲劳损伤应该是分别累积各个浪向下海况资料造成的疲劳损伤，这就导致了疲劳寿命的偏差性，并直接反映在应力参数的计算中。下面分析不同浪向下海况资料的不确定性对应力参数偏差系数η2的影响，应力参数的表达式为：

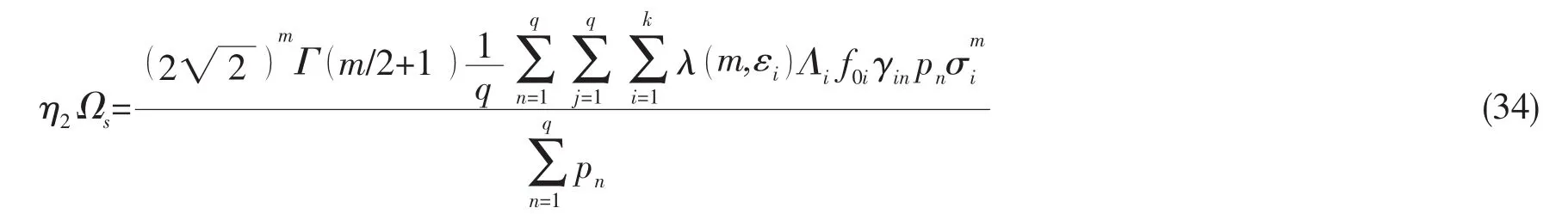
其中：Ωs为均匀迎浪角分布下使用包含所有方位的海况资料计算得到的应力参数名义值；k为短期海况数；q为浪向数；pn为浪向发生概率，见表16。

基于本节之前的分析，假设迎浪角的分布服从均匀分布，即各个浪向下的海况散布图现实出现概率均等。表17给出了采用不同浪向海况资料计算得到的结构疲劳寿命，可见东北和北方位的海况资料最为恶劣，而东南、南、西南、西和西北的海况资料较为温和。

对每个浪向下计算得到的应力参数按浪向出现概率进行加权和得到应力参数Ωa，各浪向出现概率均等时，使用包含所有浪向的那张海况散布图计算得到的应力参数为Ωs。应力参数的偏差系数η2计算公式见（35），计算结果为0.963。

表17 不同海况资料计算的疲劳寿命Tab.17 Fatigue lives of different sea states

综上所述，由与浪向有关的不确定性引起的应力参数偏差系数η为：

计算结果为0.794，可见偏差系数η＜1，说明常用的浪向均匀分布假设和直接使用全浪向海况散布图来评估结构疲劳寿命是过于保守的。

3.7 短期应力响应的不确定性

在前文引入随机变量φS描述海浪谱型的不确定性，φL描述波浪载荷传递函数的不确定性，φH描述波高的不确定性，φZ描述平均跨零周期的不确定性，φT描述短期响应总的不确定性。假设上述不确定因素相互之间是相互独立的，由于海浪谱S（ωi,Hs,Tz）与有义波高HS的平方成正比，而热点应力传递函数中只计及波浪载荷传递函数的不确定性，那么根据公式（6）短期海况下的应力响应0阶矩总偏差系数 φT为：

其均值和COV为：

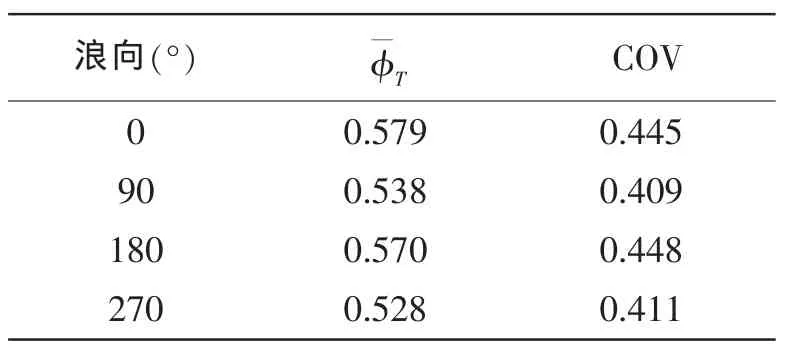
Tab.18 Mean and COV of bias φTfor short-term response

3.8 长期应力响应的不确定性

使用S-N曲线方法时，疲劳寿命计算中的应力参数计入不确定性因素后可表示为：

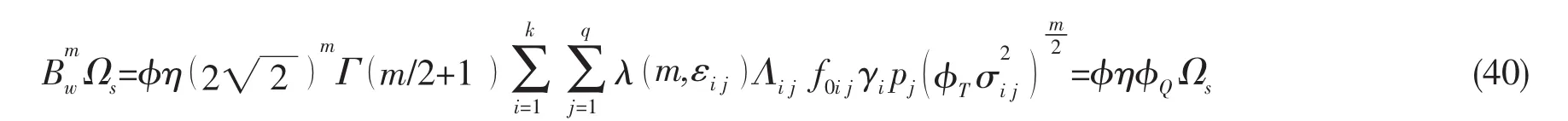
其中：Ωs为无偏应力参数名义值。针对公式（39）引入如下公式：

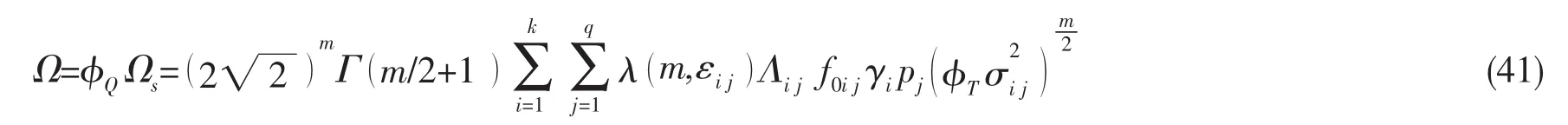
当φT取均值时，公式（41）对应的应力参数为当φT取1.0时，公式（41）为无偏的应力参数Ωs。于是可以得到应力参数的偏差系数均值为：

从公式（40）可知：

通过泰勒级数展开，本文认为Ω的均方差σΩ可表示为：

将公式（41）代入（45）中，可得到：

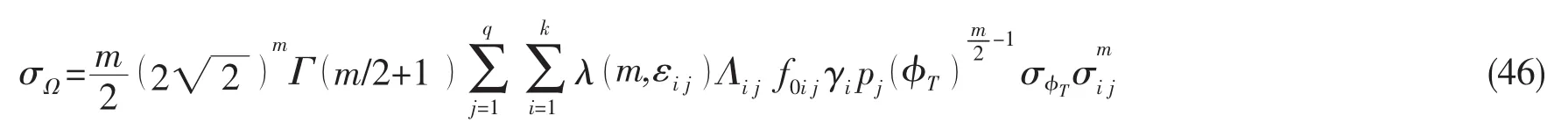
根据公式（41），φQ的均方差可以通过计算得到，计算结果为0.309。的变异系数可通过下式得到：

BW是综合考虑了对海洋波浪的描述BS和作用在结构上的波浪力的计算BF影响的随机变量，根据若干海洋石油公司给出的数据结果，可以得到BW的中值和COV的范围分别为：0.36～1.32和0.41～0.69。比较文献和本文结果可以发现本文获得的中值在前者范围中，而COV小于前者范围。这可能是因为在海况发生概率和浪向的不确定性中只计及了偏差性，而没有计及离散性即没有考虑偏差系数的变异系数。本文之所以没有考虑离散性，是因为还没有找到有关西北太平洋海况发生概率和浪向方面较多可信的统计资料。可见本文给出的疲劳寿命评估中半潜式平台的波浪载荷不确定性计算方法具有一定合理性，为波浪载荷的不确定性分析提供了较为可信的途径。

4 半潜平台典型结构疲劳可靠性分析

疲劳应力计算中的不确定性，可通过随机变量B来描述，B可写成下列乘积形式：

式中：M表示结构加工工艺；W表示海浪描述；N便是名义应力计算；H表示应力集中系数。Bi和B均服从对数正态分布。本文Bi选取结果如表19，其中BW取前文计算结果。

S-N曲线方法中，疲劳寿命的极限状态方程可以表示为：

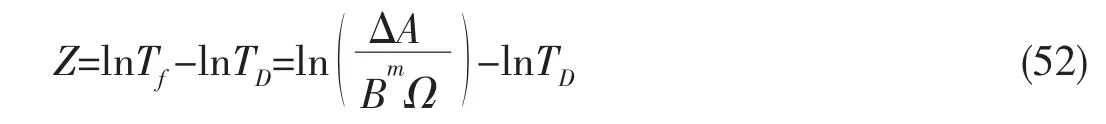
式中：△、A和B均为对数正态分布随机变量；TD为设计寿命，本平台为30年；Ω为应力参数，取无偏的确定性结果，参见公式（3），本文应力参数计算结果为616。

Wirsching[13]经过大量试验和研究后认为△服从对数正态分布，并取△的中值和变异系数分别为：和C△=0.30。DNV（2005）规范[14]中D曲线参数为

可靠性指标计算公式如下，其计算结果为2.2。

表19 Bi的选取Tab.19 Values of Bi

5 结 论

本文提出了一套疲劳波浪载荷不确定性的评估方法，主要包括海浪谱型、波浪载荷传递函数、波高和平均跨零周期、海况发生概率和浪向的不确定性及其对波浪载荷和寿命不确定性的影响。并基于载荷和强度方面的不确定性分析了半潜平台典型结构的疲劳可靠性指标。通过以上研究得出以下几点结论：（1）不同波浪载荷传递函数类型的不确定性存在较大差别；（2）南海海域的平均跨零周期修正公式与北大西洋的修正公式有较大区别；（3）不同季节的海况散布图存在较大区别，最终会导致疲劳寿命评估结果存在较大的不确定性。对于南海海域，春夏两季海况对结构的疲劳损伤贡献较小，而秋冬两季海况对结构的疲劳损伤贡献较大；（4）浪向的分布规律较为明显地影响着疲劳寿命评估结果，常用的浪向均匀分布假设和使用全浪向的海况散布图来评估结构疲劳损伤将得到过于保守的结果，浪向的实际分布规律和不确定性因素值得关注；（5）在疲劳可靠性评估中波浪载荷的不确定性统计参数均值和COV分别为0.646和0.39。

[1]Guedes Soares C.Probabilistic models for load effects in ship structures[D].Ph.D.Thesis.Norwegian Institute of Technology.NTH,Trondheim,Norway,1984.

[2]Moan T,Gao Z,Ayala-Uraga E.Uncertainty of wave-induced response of marine structures due to long-term variation of extratropical wave conditions[J].Marine Structures,2005,18:359-382.

[3]吴东伟.半潜平台结构强度可靠性评估方法研究[D].无锡:中国船舶科学研究中心,2011.

[4]杨 鹏,顾学康,吴东伟.半潜平台载荷不确定性及结构可靠性研究[J].船舶力学,2012,16(1):108-117.Yang Peng,Gu Xuekang,Wu Dongwei.Research of load uncertainty and structural reliability for semi-submersible[J].Journal of Ship Mechanics,2012,16(1):108-117.

[5]方钟圣,金承仪,缪泉明.西北太平洋波浪统计集[M].北京:国防工业出版社,1996.

[6]胡毓仁,李典庆,陈伯真.船舶与海洋工程结构疲劳可靠性分析[M].哈尔滨:哈尔滨工程大学出版社,2010.

[7]ABS.Guide for the Fatigue Assessment of Offshore Structures[S].2003.

[8]Wirsching P H,Light M C.Fatigue under wide-band random stresses[J].Journal of Structural Division,ASCE,1980,16(7):1593-1607.

[9]Haver S,Moan T.On some uncertainties related to the short term stochastic modeling of ocean waves[J].Applied Ocean Research,1983,5:93-108.

[10]DNV-RP-C103.Column-stabilized units[S].Det Norske Veritas,2005.

[11]Nolte K G.Statistical methods for determining extreme sea states[C]//POAC Conference.Reykjavik,Iceland,1973.

[12]Guedes Soares C,Ferreira A M.Analysis of the seasonality in non-stationary time series of significant wave height[J].Computational Stochastic Mechanics.Rotterdam:A A Balkema,1995:559-78.

[13]Wirsching P H.Fatigue reliability for offshore structures[J].Journal of Structural Engineering,ASCE,1984,110(10):2340-2356.

[14]DNV.Fatigue Design of Offshore Steel Structures[S].2005.