灰色理论在软基沉降预测中的应用

□吴绍祝 □吴苇琳（广州市水务规划勘测设计研究院）

普通GM(1,1)模型要求建模数据必须等时距，不得有跳跃，但在实际工程中，经常会遇到以下情况：在观测过程中，由于施工干扰，测点仪器损坏，造成数据缺失；个别数据跳跃比较大，必须剔除；沉降观测很难保证为等时距，实际操作得出的结果经常是不等时距的数列。

另外，普通GM(1,1)模型还需还原计算，数据处理量大，很多时候实际沉降的观测都是以累计沉降的形式提供的，因此普通GM(1,1)模型在很多情况下的预测效果不是很理想。基于此，文章建立了适合非等时距GM(1,1)直接模型。

1.GM（1,1）模型的建立

其时间响应序列为：

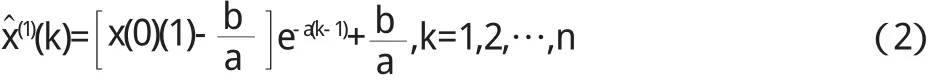
2.非等时距GM（1,1）直接模型的建立

2.1 模型的建立

文章首先将非等时距数列进行等时距处理，然后将B矩阵中的x(1)用x(0)代替，Y矩阵中的x(0)用x(-1)代替。该模型将原始数列中的数据进行一次累减生成处理。

式中：t1为首次周期观测时间，tn为距首次观测的时间间隔。

求各时间段与平均时间段的单位时段差系数μ(ti)：

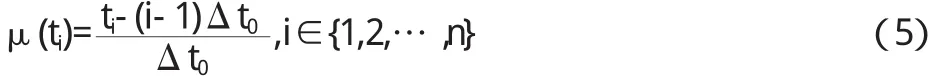
察布查尔县孙扎齐乡很多农户及贫困户都想借助发展旅游提高经济收入。乡村旅游的发展对于当地居民而言既是挑战也是契机。在众多小型旅游经营实体中，本文以“淑芬锡伯风情农家乐”作为调查对象进行系统分析。

求待定系数向量

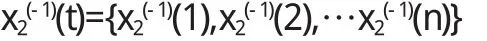
还原为与非等间隔数列中t有关的函数

为了能够与原始数列进行比较，将非等间隔序列中的时间Δt0（即k+1=t1/Δt0）带入模型，即得

因此,只需将预测时间t代入式（9）即可求得预测值。

2.2 非等时距GM(1,1)直接模型的优点

一是弱化原随机序列的随机性。二是通过此法构建的GM(1,1)克服了以往非等时距GM(1,1)模型的预测值需要还原计算、模型有时不收敛的缺点。三是在一定程度上减小了数据不全或个别数据跳跃比较大带来的预测误差。

2.3 非等时距GM(1,1)直接模型的精度检验

沉降预测模型建立后，为了对其质量进行评价，必须对它的精度进行检验，常用3种方法检验、判断模型的精度：一是残差大小检验，对模型值和实际值的误差进行逐点检验；二是关联度检验，通过考察模型值曲线与建模序列曲线的相似程度进行检验；三是后验差检验，对残差分布的统计特性进行检验。模型精度划分见表1。

表1 后验差检验模型精度等级参照表

3.工程应用

用非等时距GM(1,1)模型对某港区道路实测断面进行预测，监测点位于路基中心，实测数据见表2。利用上述方法建立了非等时距GM(1,1)模型，其拟合公式为：

另外利用了传统曲线（指数曲线）对其进行预测，其拟合公式为：

得两种模型预测值及实测值比较图如图1所示。

表2 2007年路堤沉降观测数据表（单位：mm）

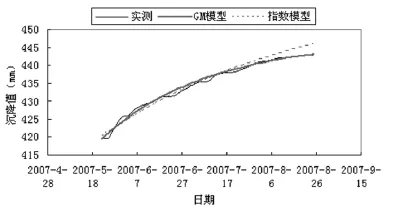
图1 断面实测值与预测值比较图

经计算可得非等时距GM(1,1)直接模型相对误差平均值为-0.0399%，指数曲线模型相对误差均值为-0.1079%，非等时距GM(1,1)直接模型预测最终沉降量为447.1684mm，指数曲线模型预测最终沉降量为460.56mm。由图1可看出非等时距GM(1,1)直接模型后期预测效果明显好于指数曲线模型，因此，文章所提出的非等时距GM(1,1)直接模型可以用于软基沉降预测，并且结果是可靠的。

4.结论

文章对于软土地基由累计沉降作为原始数列建立的非等时距GM(1,1)直接模型的预测值与实测值相比结果相当吻合，并与传统的指数模型进行对比，表明模型是精确可靠的，并克服了以往非等时距GM(1,1)模型的预测值需要还原计算、模型有时不收敛的缺点。

综上所述，采用本文的等时距GM(1,1)直接模型预测软基沉降，方法可行，而且效果比较理想。可以对软土工程进一步施工时控制填筑速率以及推测沉降规律和沉降量等提供参考，对软土工程的设计、施工、校核都有指导意义。

[1]兰孝奇，严红萍，刘精攀.灰色系统预测模型在沉降监测中的应用[J].现代测绘，2006，1.

[2]陈伟清.建筑物沉降数据分析的灰色预测方法[J].测绘技术装备，2005，4.

[3]田江磊.灰色理论在高等级公路填方路基质量控制中的应用[硕士学位论文].西安:长安大学，2005，31-37.

[4]杜海伟，张建军，李新生，张丽萍.地基沉降计算指数曲线配合法及其应用.土工基础，2005，1.