水工建筑地下结构抗震特点及分析方法概述

□王 磊（黄河勘测规划设计有限公司）

目前，随着水利工程大范围的展开，水工建筑物的结构中地下结构被广泛用于各个工程建设当中，并且其规模有日益扩大的趋势。但从地质构造上说，虽然我国国土幅员辽阔，但是基本处于欧亚大陆与印度板块之间，自古以来就是地震活动的多发区，处于地震基本烈度为七度或者高于七度的地震区城市几乎占我国城市总量的一半。由此可见，关于地下结构抗震设计对于城市建筑物以及人员、财产安全的重要性。

1.地下结构的地震反应特点

根据我国相关地震资料可知，地震对地下结构影响极大，即使约7级地震就有过地下隧洞被地震影响破坏的情况出现。通过分析可知建筑物的地下结构和地上结构在地震影响下所产生的振动特性有很多不同之处，主要由以下几个方面：

首先在应变方面，地下结构在地震影响下其震动变形往往受到建筑物地基约束影响较大，自振特性在动力反应中表现不明显，应变和地基土体的变形有较大联系,但是地面建筑物产生的震动变形尤其是在低阶状态下反应则十分明显。

其次，在地震波对震动形态的影响方面，地震波会对地下结构的震动形态产生很大影响，即使地震波入射方向未发生较大变化，其变形、应力等方面也有很大变化,而地上建筑物结构在相同情况下变形、应力等方面受到的影响相对于地下结构则很小。

另外，在地震影响下，地下结构的反应往往受到周围土体相互作用的影响较大，其尺寸、埋深程度都会对结构中点的相位差有较大影响。

所以，尽管在地震波影响下，地下结构和地上建筑物均会产生较大应力反应，产生变形、位移等情况，但是地下结构的影响变形主要来自地基以及地基周围土体的运动特性和相互作用。而地上建筑的影响变化则主要来自结构自身的质量、尺寸、强度变化。

2.地下结构抗震基本分析方法

对于地下结构抗震分析研究一般分为地震观测、实验研究、理论分析等，但是由于地质条件的原因，地下结构的形式也是各种各样。

上述方法各有特点，目前在各自不同的适用场合的地下结构设计计算中这些方法都发挥着良好的作用。地下结构通常都延伸很长的距离，沿线的地形地质条件发生很复杂的变化，地下结构的形式也多种多样，为了考虑这些因素的影响，进行地下结构的抗震设计，在上述基本方法的基础上发展了许多地下结构抗震分析的实用方法，主要有BRAT法、反应位移法、等效静力荷载法、福季耶娃法、动力有限元法等。

2.1 BART法

BRAT法来源于美国，1960年美国在旧金山修建海湾地区快速运输系统(简称BART)地下结构时所采用的抗震设计准则。其主要设计思路是利用地下结构的影响变形主要来自地基以及地基周围土体的运动特性和相互作用的原理，用地基周围土体的韧性来约束结构变形，而不是单纯依靠结构单元体来抵抗结构的变形。通过这种设计思路，可以在设计中充分利用因地震引起的地层振动特性的迅速确定性，从而提供设计依据。

2.2 反应位移法

反应位移法是日本学者在20世纪70年代提出的。该理论基本原理是以弹性地基梁代替地下线状结构物进行地震模拟计算，在地震情况下地基位移对弹性地基梁上的作用以及弹性地基梁响应结果，从而计算出地下结构相应的反应，计算公式：

注：K包括地下结构的刚度K和地基弹性抗力系数K，为结构所在位置土介质的地震变位。

2.3 等效静力荷载法

等效静力荷载法的计算思路是将地下结构因为地震加速度的作用而产生的惯性力作为荷载，并计算在该荷载的作用下结构发生的应力变化，从而判定地下结构抗震性能的一种计算方法。

等效静力荷载法略微保守，主要用于受惯性力影响较大浅埋结构计算。计算公式为：

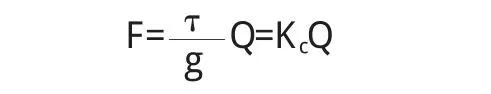
式中：Q—结构物的重量；τ—作用于结构的地震加速度；g—重力加速度；K—地面运动加速度峰值与重力加速度g的比值。

在进行地下结构的计算过程中，应将在地震条件下计算对象自身以及上覆土的惯性力、土压力、内部液体的动压力等因素考虑在计算范围之内。

2.4 福季耶娃法

该计算方法由前苏联学者福季耶娃提出，是一种拟静力的计算方法。其基本思路为假设在结构围岩介质均为线弹性体情况下，由于地震作用而引起围岩应力和衬砌内力计算，为有加固孔口周围应力集中的线弹性理论动力学问题的求解。

无限远受到的双向压(拉)应力：

注:K为地震系数(与地震烈度有关);T为岩石质点震动的卓越周期。

在波长较大的剪切波作用下，介质在无限远处受到的与对称竖轴成角方向的纯剪力为：

将上述两式求解，即可得结果：在给定的组合情况T下，压缩波与剪切波以及拉伸波与剪切波共同作用的场地总应力及衬砌总内力值，再将其重力场叠加，可得结果。

2.5 动力有限元法

该计算方法虽然思路早在20世纪40年代就有人提出，可真正在工程设计中使用是在计算机被大规模用于工程设计后，而将有限元分析（FEA，FiniteElementAnalysis）应用到地下结构的抗震设计中，将计算对象看成有许多有限元组成的结构，充分考虑边界条件等多方面因素，将地震波输入后分析结构的动力响应，计算底层与结构的变形、应力、应变时刻变化，进而推导该条件下的满足条件。动力有限元法不但可以显著提高计算精度，而且可以适应各种复杂地质情况，从而逐步成为主要的抗震分析手段。

随着有限元计算技术的发展，尤其是动力有限元的发展，使有限元成为抗震分析的有效途径之一。该方法将包含对象结构物在内的整个地层划分成有限元网格，考虑边界条件以后，输入地震波，进行动力响应分析，从而得出每一时刻地层和结构物中的变形、应力和应变等。可以适用于各种复杂形状的连续体问题，能较好的反映各种复杂的材料特性，并且随着数值计算技术的不断完善和计算机内存及速度的不断提高，动力有限元的应用越来越多，逐渐发展起来。

3.结论

由于地质情况的多变以及地震条件产生的复杂，地下结构的影响分析限制很多，上述各种分析计算方法虽然都由研究者通过实践分析得来，但是都存在着一定的不足。而就当前科技发展的情况看，地下结构的抗震设计仍然是设计的难点之一，我国周边国家的地震所造成的经济和人员的损失都给我们以重要的启示，就目前我国的地下结构尤其是水利工程的抗震设计情况来看，存在设计规范较少等情况，所以文章针对目前水利工程地下结构抗震的设计特点和分析进行简单论述和分析，希望能对此方面的研究提供一定帮助。

[1]福季耶娃著.地震区地下结构的支护计算[M].徐显毅译.北京：煤炭出版社，1986.

[2]郑永来，杨林德.地下结构抗震[M]，上海:同济大学出版社.

[3]林皋.地下结构抗震分析综述（上）[J].世界地震工程，1998（2）：1～10.

[4]林皋.地下结构抗震分析综述（下）[J].世界地震工程，1998（3）：1～10.

[5]林皋，梁青槐.地下结构的抗震设计[J].土木工程学报，1996，29（1）：15－24.

[6]常虹.地下建筑结构抗震设计的几个问题[J].吉林建筑工程学院学报，2005，No1.