基于概率密度的短波OFDM信号识别方法*
付哥佳,段田东,刘瑞东,徐文艳
(信息工程大学 信息系统工程学院,河南 郑州 450002)
利用高阶混合矩和累积量特征对信号进行盲识别,一直是信号类型识别的主要方式之一。近年来随着多载波技术的应用,该方法也逐渐应用于自动区分OFDM信号与单载波信号上。许多科研工作者都对此问题进行了分析,并且提出了多种混合矩的方法。
OFDM信号的概率密度服从正态分布,对其进行盲识别的理论最早是由AKMOUCHE W提出的[1],但是该算法复杂度较高。2002年GRIMALDITI D提出了一种不需要预先知道符号周期和计算协方差矩阵的改进算法[2],利用信号的采样点数代替信号的符号周期并省略了协方差的计算,根据时延的不同构成四阶累积量的向量,然后利用向量内积判断OFDM信号,最后估计OFDM信号参数对检测结果进行检验。但是OFDM信号并非服从完全的高斯分布,它的四阶累积量的值还与信道、信号本身的能量相关,并且信道和信号能量在不同条件下是不定值,因此即使信号服从类高斯,其四阶累积量也不是一个固定值。于是Wang Bin[3]基于OFDM信号具有高斯性的特点,利用归一化峰度和混合矩提出了一种新的算法,该算法能消除信号能量对四阶累计量的影响,较好地对OFDM信号进行分类。刘献玲等[4-7]使OFDM信号盲识别理论得到了进一步发展。本文从信号概率密度的角度将这些方法进行统一的阐释,阐述各种方法的本质,对以往研究中的不足加以修正,并提出一种通用的高阶混合矩模型。
1 系统模型及问题描述
1.1 信号模型
假设信号 x(t)经过信道传输后,接收信号为y(t),其表达式为:

其中,x(t)是输入信号,h(t)代表信号经过的信道,y(t)代表输出信号,n(t)代表加性高斯白噪声,均值为 0,方差为 σn2。 本文主要对 MPSK、MFSK、QAM和 OFDM信号进行研究。其各类信号的基本表达式如下[8]:
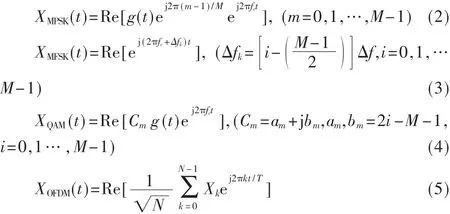
以上各式均为单个码元符号的表达式,其中0≤t≤T,g(t)代表平方根升余弦函数,fc代表信号中心频率,Δfk代表FSK信号中传输信号的频偏,Cm代表QAM信号的符号映射。
1.2 归一化峰度和六阶混合矩
信号的归一化峰度定义为[9]:

[3]根据归一化峰度的概念,提出了一种六阶混合矩的方法,其定义如下:

2 归一化峰度及混合矩特征
本文从信号的概率密度出发,通过假设和推论各类信号的概率密度,对参考文献[3]中没有讨论的MPSK、MFSK实信号的归一化峰度、没有考虑成型滤波对MPSK归一化峰度的影响的不足给予修正和补充,重新确定信号的归一化峰度和混合矩等特征值。由于信号的实信号和复信号服从的概率分布并不一致,本文将分实信号和复信号两种情况对信号进行讨论,最后提出一种通用的高阶混和矩,并说明高阶混合矩的优点。
2.1 各类信号的概率密度
根据MFSK信号模型可以看出,由于MFSK信号是由不同频率的正弦信号组成,所以MFSK信号也服从正弦信号概率密度分布。MPSK信号主要是先生成等幅度的相位映射,然后插零,利用成型脉冲对信号进行成型,最后搬移信号到中心频率上。从MPSK的生成过程可以看出,MPSK在原始的基带上服从均匀的相位分布,所以其服从类均匀分布。QAM信号调制原理与MPSK信号一致,但是其符号映射并不是在一个圆上,并不服从均匀分布。OFDM信号从理论上将是多个正交信号相加,这些正交信号具有相同的均值方差且正交信号相互独立。因此根据中心极限定理,OFDM信号概率密度接近于高斯分布。各类实信号的概率密度如表1所示。
2.2 实信号和复信号归一化峰度及六阶混合矩的值
2.2.1 实信号的归一化峰度及六阶混合矩
根据参考文献[9],高斯信号的K阶中心矩表示为:

其中X为信号样本,mx为均值。由于OFDM信号的概率密度近似高斯分布,因此,OFDM的归一化峰值近似为3,六阶混合矩近似为15。

表1 各类信号的概率密度
对于MPSK信号,由于其服从均匀分布,所以根据表1的概率密度函数,其K阶中心矩为:

因此,根据式(6)、式(7),均匀分布的归一化峰值近似为1.8,六阶混合矩近似为3.88。对于采样率为12 000 Hz、中心频率 2 400 Hz、码元速率为2 400 Bd的 BPSK、QPSK、8PSK信号,对2 048点进行统计平均,其归一化峰值及六阶混合矩如表2所示。将之与理论值对比,说明MPSK近似服从均匀分布。

表2 实信号K6x与Kx的实测值
对于MFSK信号,由于MFSK信号是由不同频率的正弦信号组成,且各个正弦信号的出现时间有先后次序,又因为正弦信号服从同样的正弦信号概率密度分布,所以MFSK信号也服从正弦信号概率密度分布。根据表1的概率密度函数,其二阶、四阶、六阶的中心矩如下:
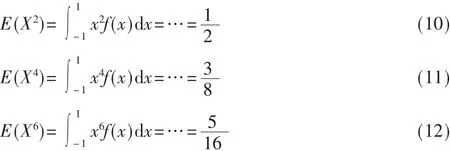
因此对于正弦信号其归一化峰值近似为1.5,六阶混合矩近似为2.5。
对于QAM信号,其星座映射并不服从均匀分布,并由于成型脉冲影响,其概率密度既不完全服从均匀分布,又不完全服从正弦分布。对于采样率为12 000 Hz、中心频率2 400 Hz、码元速率为2 400 Bd的 16QAM和 32QAM信号,对2 048点进行统计平均。16QAM其归一化峰度为1.54,六阶混合矩为2.6;32QAM的归一化峰度为1.33,六阶混合矩为 1.87。
2.2.2 复信号的归一化峰度及六阶混合矩
对于OFDM信号,其复信号表示为:

由于xrofdm和xiofdm是零均值且统计独立的从高斯变量,且方差相同,Xcofdm满足:

根据瑞利分布的定义,Xcofdm的偶数次矩应与瑞利分布偶数次矩相同,满足:

其中 Γ(p)=p!,因此根据式(6)、式(7),OFDM 复信号的归一化峰值近似为2,六阶混合矩近似为 6。
对于MFSK信号,由于其实部满足正弦分布,因此其复信号应与复指数信号的K阶矩相同。复指数信号的K次幂仍为复指数。因此复指数信号的各阶矩只与正弦信号的幅度有关,假设复指数信号的二阶矩能量为E,则:

因此对于复MFSK信号,其归一化峰度近似为1,六阶混合矩近似为1。
对于MPSK与QAM信号,由于不能确定其复信号的密度,所以其归一化峰度和六阶混合矩以实际测量为准。对于采样率为12 000 Hz、中心频率 2 400 Hz、码元速率为2 400 Bd 的 BPSK、QPSK、8PSK、16QAM、32QAM 信 号,对2 048点进行统计平均,其统计特征如表3所示。
2.3 通用高阶混合矩
较之信号四阶累积量同时受信道和信号本身能量影响,信号的归一化峰度特征不受信号能量的影响,具有更精确的特点。本文根据归一化峰度和六阶混合矩,提出一种通用的克服信号本身能量干扰的通用高阶混合矩:

表3 复信号K6x与Kx的实测值

其中2n代表高阶混合矩的阶数,高阶混合矩的优势为高斯信号随着混合矩阶数增加,其混合矩特征值较其他信号特征值增加得更快,因此OFDM与其他信号区分的特征值之间距离更大,这样利于门限的选择,减少干扰对高阶混合矩特征值的影响。
3 仿真与实验分析
实验前期准备:产生采样率Fs=6 600 Hz,有效DFT点数为ND=60,循环前缀点数NG=28,子载波带宽为110,码元速率 Ts=75,符号映射为DQPSK的OFDM信号。产生 Fs=8 000 Hz,频移为 200 Hz,码元速率为100 Bd,载波频率为 2 000 Hz的 2FSK、4FSK、8FSK信号,产生采样率为1 2000 Hz、中心频率 2 400 Hz、码元速率为 2 400 Bd的 BPSK、QPSK、8PSK、16QAM 和 32QAM 信号。
3.1 识别OFDM信号
本文针对短波信道对其算法性能进行分析。短波信道的参数根据ITU-520-1中规定的好、中、差短波信道标准[10-11]来选择,信道模型根据参考文献[12],使用2径的Watterson信道模型。针对不同信道条件,在不同信噪比下对各类实信号的归一化峰度及六阶混合矩进行对比,其实验结果如图1所示。结果表明在短波信道条件下,利用混合矩理论选择合适的混合矩特征值,能够较好地识别OFDM信号。在归一化峰度门限选择2.4、六阶混合矩门限选择9的情况下,利用两种参数进行联合估计,OFDM信号在各种短波信道的识别率如图2所示。


3.2 高阶混合矩的优势
为了测试通用高阶混合矩对OFDM信号类型识别产生的影响,本文对各类实信号各阶混合矩在无噪声及无信道干扰条件下的实测值进行比较,实验结果如图3所示。图3说明,在无干扰的情况下,OFDM信号的各阶混合矩增加速度远远大于其他信号,混合矩阶数越高,其特征值间隔越大,其门限特征更易设置,干扰对高阶混合矩特征值影响减弱,更利于识别OFDM信号。
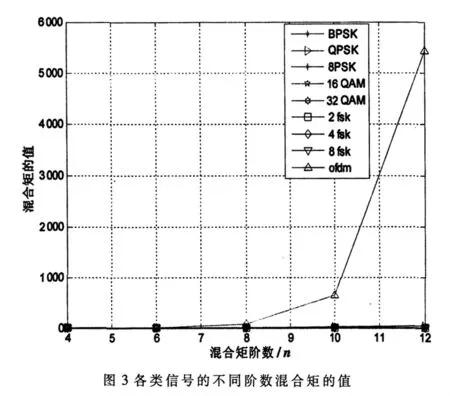
本文利用各类信号的概率密度对其归一化峰度与六阶混合矩重新进行了阐释,对实信号的归一化峰度和六阶混合矩给出了补充说明。提出了通用的高阶混合矩特征,实验证明高阶混合矩除了具有低阶混合矩能够识别OFDM信号的特点外,还具有门限更易设置、抗干扰能力更强的优点。
参考文献
[1]WALTER A.Detection of multicarrier modulations using 4th-order cumulants[C].IEEE MILCOM,1999:432-436.
[2]GRIMALD D,RAPUANO S,TRUGLIA G.An automatic digital modulation classifier for measurement on telecommunication networks[C].Proc of IMTC2002.Anchrage,Ak,USA:IEEE,2002:957-962.
[3]WANG B,GE L.A novel algorithm for identification of OFDM signal[A].Proc.IEEE WCNC[C].2005:261-264.
[4]刘献玲,陈健,阔永红,等.基于累积量的OFDM调制识别[J].电子科技,2007(02):29-32.
[5]吕挺岑,李兵兵,董刚.一种多径信道下的OFDM信号盲识别算法[J].现代电子技术,2007(11):13-16.
[6]KANTERAKIS E,Wei Su.OFDM signal classification in frequency selective rayleigh channels[C].IEEE MILCOM,2011:1-6.
[7]EL-KHAMY S E,ELSAYED H A,RIZK M M.C45 classification of OFDM signals using higher order statistics and clustering techniques[C].Radio Science Conference(NRSC),Publication Year:2012:541-549.
[8]PROAKIS J G.Digital communication(Fourth Edition)[M].New York,McGraw-Hill,2008.
[9]张贤达.现代信号处理[M].北京:清华大学出版社,2002.
[10]ITU.Recommendation 520-1 Use of high frequency ionospheric channel simulators[R].Recommendations and Reports of the CCIR,1986,3:57-58.
[11]ITU.HF Ionospheric Channel Simulators,CCIR Report 549-2[R].Recommendations and Reports of the CCIR,1986,3:59-67.
[12]WATTERSON C,JUROSHER J R,BENSEMA W D.Experimental confirmation of an HF channel model[J].IEEE Trans on Communication Technology,1970,18(6):792-803.

