折叠偶极子阵列无芯标签极点特性分析*

何 毅,徐 利,邹传云

(1.西南科技大学 网络信息中心，四川 绵阳 621010；2.西南科技大学 信息工程学院，四川 绵阳 621010)

随着射频识别RFID(Radio Frequency Identification)技术的发展及物联网时代的到来，射频识别标签在生活中的应用将越来越广泛[1]。传统电子标签的功率需求大、单片价格高、工作距离短等问题是制约电子标签大力发展的瓶颈所在。针对这些问题，国内外已有很多学者展开对无芯片射频标签的研究[2-4]。

目标极点是雷达系统中实现目标识别的重要参数。在谐振域，目标的瞬态电磁散射响应可以由其自然谐振极点以极点展开法SEM(Singularity Expansion Method)[5]的形式来表征。无芯标签内部不包含任何集成芯片及连接组件，是一种特定的金属结构，可以通过标签结构对入射电磁波的散射特性提取标签极点，实现目标识别。矩阵束算法有较强的数据拟合及噪声抑制能力，在极点提取算法中得到广泛应用[6-7]。

复平面(S平面)内的极点分布能提供目标的基本形状、尺寸、组成材料等识别信息，因此，极点特性的准确提取是目标识别的决定因素。无芯片射频标签极点参数的准确提取一方面受算法精度的影响(这可通过优化算法[6]的方法实现)；另一方面受到无耗电介质材料(介质厚度、相对介电常数)的影响。本文以折叠偶极子阵列无芯标签为研究对象，通过对导体结构的极点提取，分析了电介质作为标签衬底对极点分布特征的影响。

1 折叠偶极子阵列无芯标签极点特性

目标极点可由矩阵束算法在目标时域电磁散射响应中获得。根据极点展开法，目标瞬态电磁散射时响应的信号模型可以表示为:

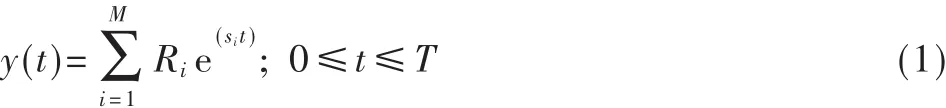
式中T为时间信号长度；M为信号模型的模数亦即极点对数；si=αi+jωi表示 S平面内的 i阶共轭复极点,虚部参数 ωi是谐振角频率，实部 αi为衰减因子，取负值；Ri为对应于i阶复极点的留数。

图1所示折叠偶极子阵列无芯标签由5个不同尺寸的偶极子谐振单元组成,各谐振单元尺寸如表1所示。

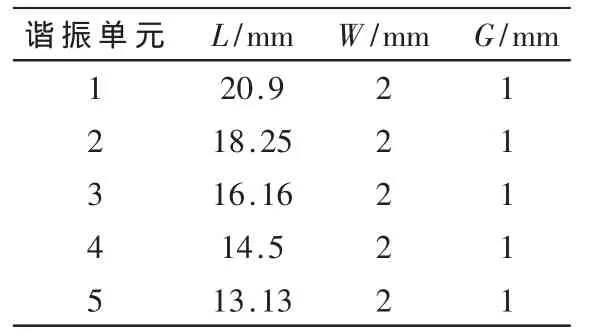
表1 谐振单元结构尺寸

在自由空间中，利用FEKO软件施加图1所示的入射平面波 (入射方向垂直纸面向内，平行纸面方向极化)，设置频率范围为 250 MHz～6 GHz，计算频点 500，由此得到频率响应,如图2所示。

对由图2所示的频率曲线做IFFT变换获得时域散射响应，利用矩阵束算法提取标签极点如图3。由于极点以共轭对出现，且衰减因子为负值，因此只给出了一个象限内的极点分布。

图3中的极点数目对应标签结构中的谐振单元数目，每个极点参数取决于谐振单元的谐振特性，不同标签结构的极点分布状态不同。

2 标签极点分布的影响因素

无芯标签极点是实现标签识别的重要参数，本文探讨了电介质材料（介质厚度、相对介电常数）对无芯标签极点分布的影响。

2.1 介质厚度对极点分布的影响

对图1所示的标签结构加上无耗电介质衬底 (如图4)，分析不同介质厚度d对极点分布的影响。

设定介质材料相对介电常数2，厚度d从0.1 mm到0.5 mm以步长0.2递增。在相同的入射平面波及频率范围内，图5给出了无芯标签极点分布随介质衬底厚度d的变化规律(d=0表示没有添加介质)。

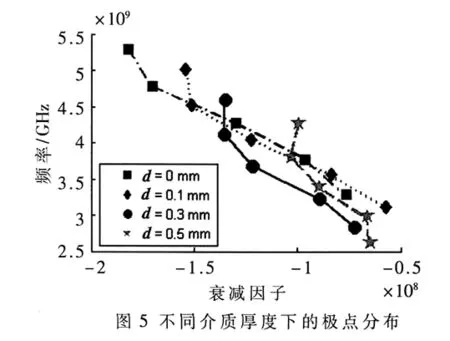
由图5可知，随着d的增加，标签结构对应的极点分布以类S型曲线向坐标原点靠近，其衰减因子αi和谐振频率ωi呈现变小的趋势。

衰减因子αi是由目标表面及内部介质体的损耗引起的，导体表面越大，衰减越大。当为标签加上无耗介质衬底后，由于金属标签相对表面减小，加上介质体的低损耗特性，使得衰减因子αi变小。

图5表明，在本文的参数设置下，为了获得无芯标签较为明确的极点分布，介质材料选定后，介质厚度d可在0.1 mm～0.3 mm范围内。

2.2 相对介电常数对极点分布的影响

相对介电常数是介质体的重要参数之一，本节将在介质衬底厚度d一定时，分析介质相对介电常数e对目标极点分布的影响。设定d=3 mm，相对介电常数e从0～6以步长2递增。对图4所示的介质标签施加相同的源激励，在相同的频率范围内，图6给出了相应的极点分布规律。

由6可以看出，相对介电常数对标签极点分布的影响与介质厚度的影响基本一致。随着相对介电常数的不断增加，极点分布状态仍以类S曲线向坐标原点靠近，衰减因子αi和谐振频率ωi也呈现逐渐减小的趋势。

图6表明，在介质体厚度不变的情况下，相对介电常数e介于2～4之间,能得到较为明确的极点分布规律。

以上结果表明，介质体厚度及相对介电常数对标签极点分布均有影响，后者较前者的影响更大。需要指出的是，以上分析是以折叠偶极子阵列无芯标签为载体进行的，然而对其他目标结构[8-9]的分析也能得到类似的结果。

极点特征是目标识别方式的重要参数，极点提取的准确性受到目标结构、入射波频率、提取算法、使用环境等多种因素的影响。本文以折叠偶极子阵列无芯标签为依托，结合实际应用需求，主要分析了无耗电介质参数对标签结构极点分布的影响。研究结果对通过目标极点分布规律选择适当的介质载体材料具有重要指导意义，在某种程度上这将有助于推动无芯标签在RFID系统中的应用。

[1]董丽华,等编著.RFID技术与应用[M].北京：电子工业出版社，2008.

[2]MUKERJEE S.Chipless radio frequency identification by remote measurement of complex impedance[C].in Wireless Technologies,2007 European Conference on,2007:249-252.

[3]PRERADOVIC S.BALBIN I,KARMAKAR N C,et al.A novel chipless RFID system based on planar multiresonators for barcode replacement[C].2008 IEEE International Conference on RFID,Nevada USA April 16-17,2008:289-296.

[4]MANTEGHI M,SAMII Y R.Frequency notched UWB elliptical dipole tag with multi-bit data scattering properties[C].in Antennas and Propagation Society International Symposium,2007 IEEE,San Diego,CA,2007:789-792.

[5]BAUM C E.The singularity expansion method:Background and developments[J].Antennas and Propagation Society Newsletter,IEEE.1986(28):14-23.

[6]WANG S,GAUN X,WANG D,et al.Application of matrix pencil method for estimating natural resonance of scatters[J].Electronics Letters,2007(43):3-5.

[7]GRANT L L.Comparison of matrix pencil and prony analysis for estimating electromechanical modes in noisy signals for power system applications[D].MS Thesis,Missouri University of Science&Technology,Rolla,2011.

[8]BLISCHAK A,MANTEGHI M.Pole residue techniques for chipless RFID detection[C].in Antennas and Propagation Society International Symposium,2009.APSURSI′09.IEEE,2009:1-4.

[9]CHAUVEAU J,BEAUCOUDREY N,SAILLARD J.Selection of contributing natural poles for the characterization of perfectly conducting targets in resonance region[J].IEEE Transactions on Antennas and Propagation,2007,55(9).