大地高误差对坐标系转换精度的影响

王明孝，陈建斌，赵秀杰，曹学诚

（68029部队，甘肃 兰州 730020）

在GPS外业测量中，通过相对定位获取的地面点坐标通常都是ITRF坐标或WGS－84坐标，基于全球大地坐标框架。而实际工程项目通常基于局部椭球，其椭球参数、定位、定向与ITRF（或WGS－84）椭球不同，需要通过坐标系变换将ITRF坐标（或WGS－84坐标）转换为当地坐标系坐标（如北京54）。

坐标系转换需要3个以上地面点在不同参考椭球上三维空间直角坐标（即重合点三维空间直角坐标）。当转换涉及到参心坐标系（如北京54、西安80），并且坐标与地图有关时，其坐标形式通常是分带的高斯平面坐标加正常高（x，y，h），坐标转换需要以北京54（或西安80）参考椭球面为过渡，将重合点的北京54（或西安80）坐标转换为三维空间直角坐标（X，Y，Z）。为叙述方便，局部椭球上的坐标加下标54，ITRF或WGS－84椭球上的坐标加下标84。则由（x54，y54，h常）计 算（X54，Y54，Z54）的 步骤为

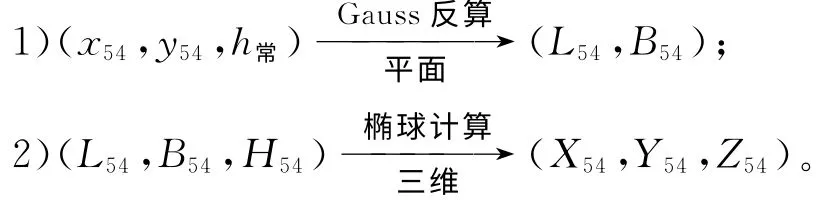
由于地面点的北京54椭球高H54很难精确获得，上述第2步即椭球计算时通常用HWGS84或h54＋ζ来近似代替H54。大地高误差会影响三维空间直角坐标（X54，Y54，Z54）的精度。

椭球变换时，首先利用重合点的空间直角坐标（X54，Y54，Z54）、（X84，Y84，Z84）计 算 一 组 转 换 参 数（4个参数或7个参数）；再根据转换参数计算一定区域内已知点在另一椭球上的坐标。

1 广义空间直角坐标变换

WGS－84空间直角坐标与本地坐标系空间直角坐标通过广义空间直角坐标变换公式实现相互变换。两个空间直角坐标变换的原理如图1、式（1）所示。

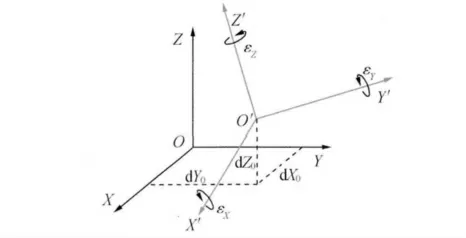
图1 两个空间直角坐标系变换

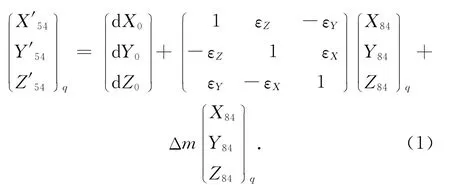
式中：dX0，dY0，dZ0是3个线元素，εX，εY，εZ是3个角元素，Δm是尺度元素。

2 大地高误差的影响

2.1 转换参数误差

北京54高斯平面、正常高以参考椭球面为过渡，转换为空间直角坐标共两个步骤，其中第2步是由大地坐标求空间直角坐标，其转换公式为（省略下标54）

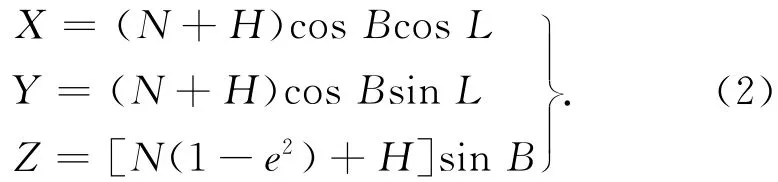
重合点的大地高用HWGS84或h54＋ζ来近似代替时的误差计为ΔH，对H求微分得

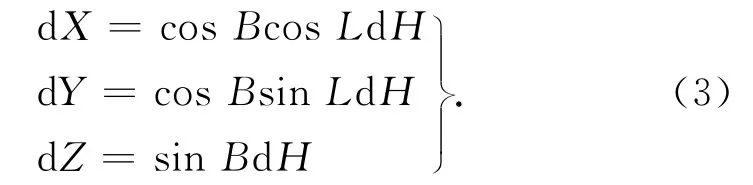
当B＝35°，L＝120°时，dX＝－0.41dH，dY＝0.71dH，dZ＝0.57dH。

根据广义空间直角坐标变换公式得

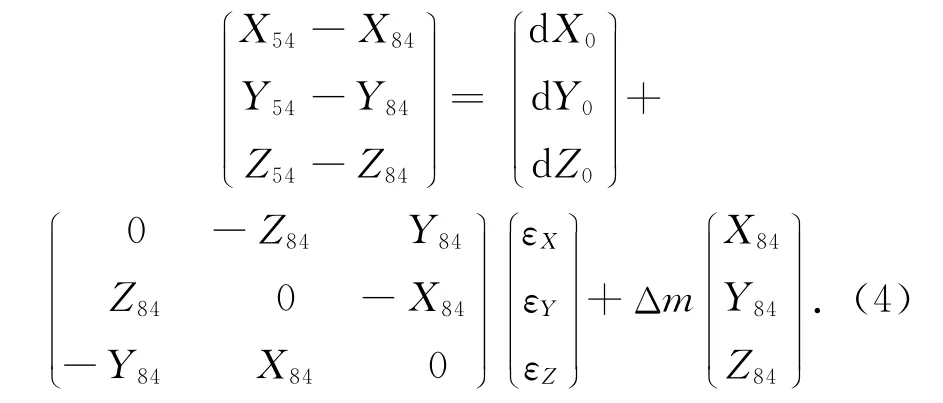
若计系数矩阵

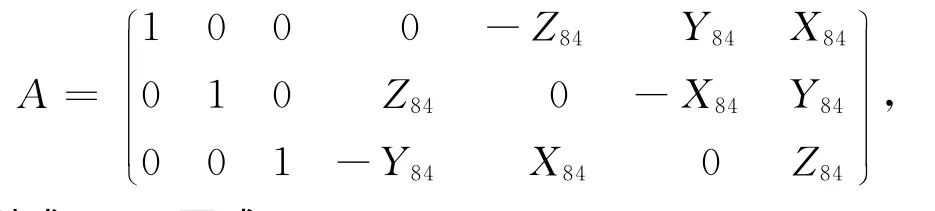
则式（4）可写成

其中转换参数

在河北农业大学校园漫游APP搭建完成后，在固定位置和走廊墙壁上等位置设立宣传展板，宣传李保国精神、太行山精神、9301班精神等河北农业大学的传统文化，并定期进行更新，但是旧宣传展板不删除，采取覆盖模式，同学们可以向前翻阅学习河北农业大学的传统文化精神。

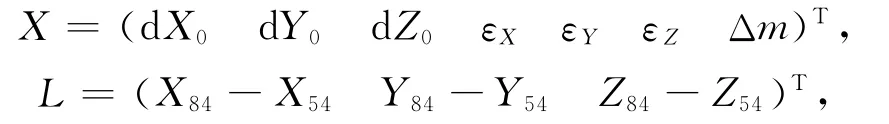
则法方程为

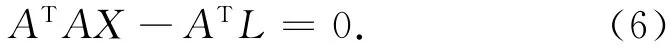
X的解为

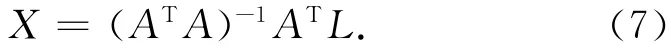
由式（3）

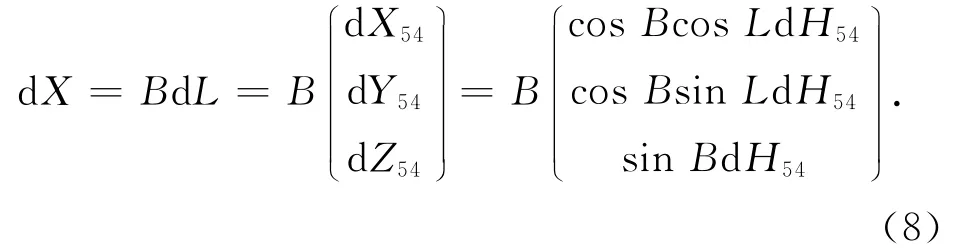
其中B＝（ATA）－1AT。式（8）即为重合点的大地高误差引起的转换参数误差。

本文选取了新疆哈密某测区进行试验，计算七参数的重合点共3个，当用84大地高、54正常高、84大地高加100m、84大地高减100m代替54大地高时，分别求得的七参数如表1所示。

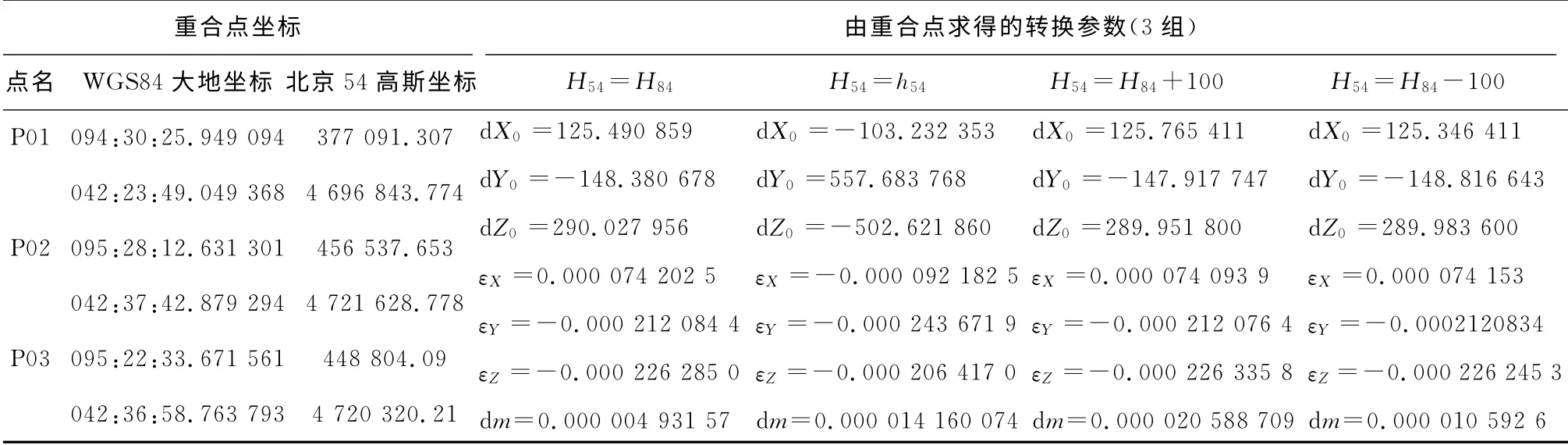
表1 重合点大地高误差对七参数的影响

4组结果数据的差别较大，尤其是用54正常高代替大地高时，得到的七参数与其他3组存在系统性偏差。

2.2 目标坐标误差

根据2.1中求得的转换参数，对外业测量得到的ITRF坐标或WGS－84坐标由式（2）可得到局部椭球上的空间直角坐标。式（2）可写成

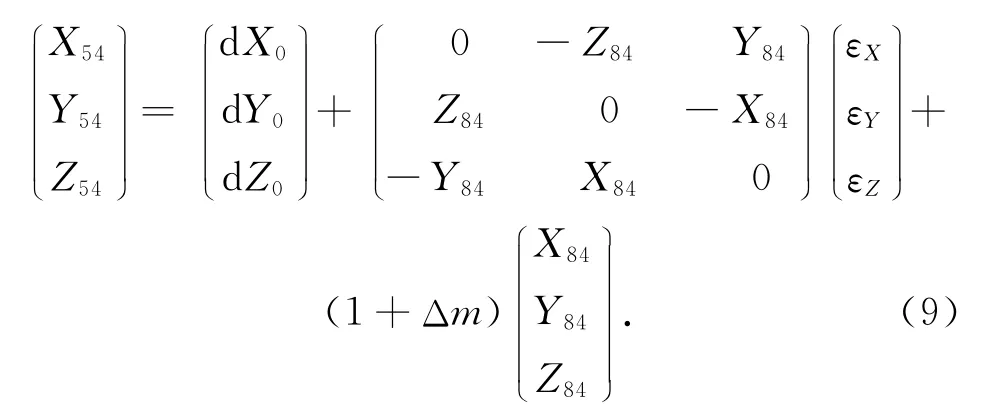
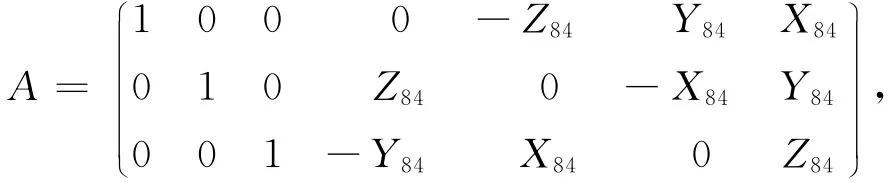
则式（9）可写成

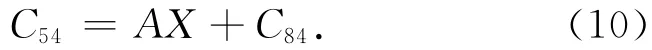
其中转换参数

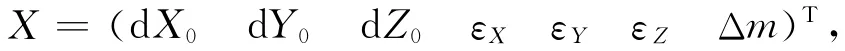
局部椭球上的空间直角坐标：C54＝（X54Y54Z54）T，全球椭球上的空间直角坐标C84＝（X84Y84Z84）T。

式（10）对X求微分得

由式（8）得

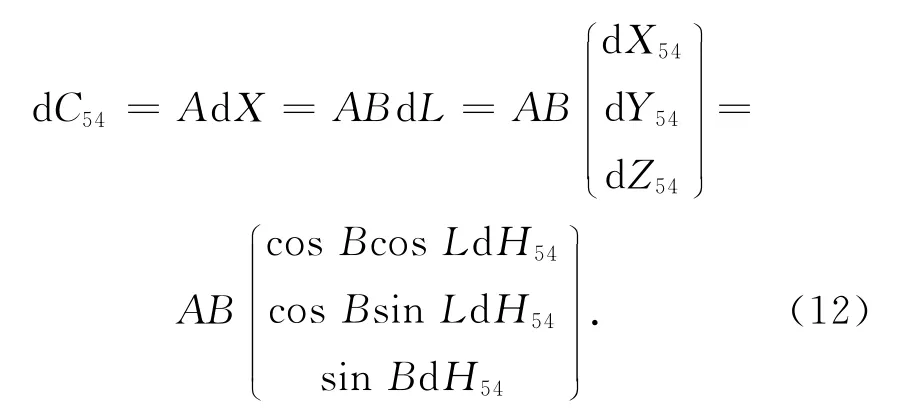
此即为重合点的大地高误差引起的其它点的目标坐标系坐标误差。

对测区内其余10个点利用表1的4组七参数进行转换，得到的结果如表2所示。4组结果与原北京54高斯坐标差值很小，误差方差约在0.000 7、0.000 2。

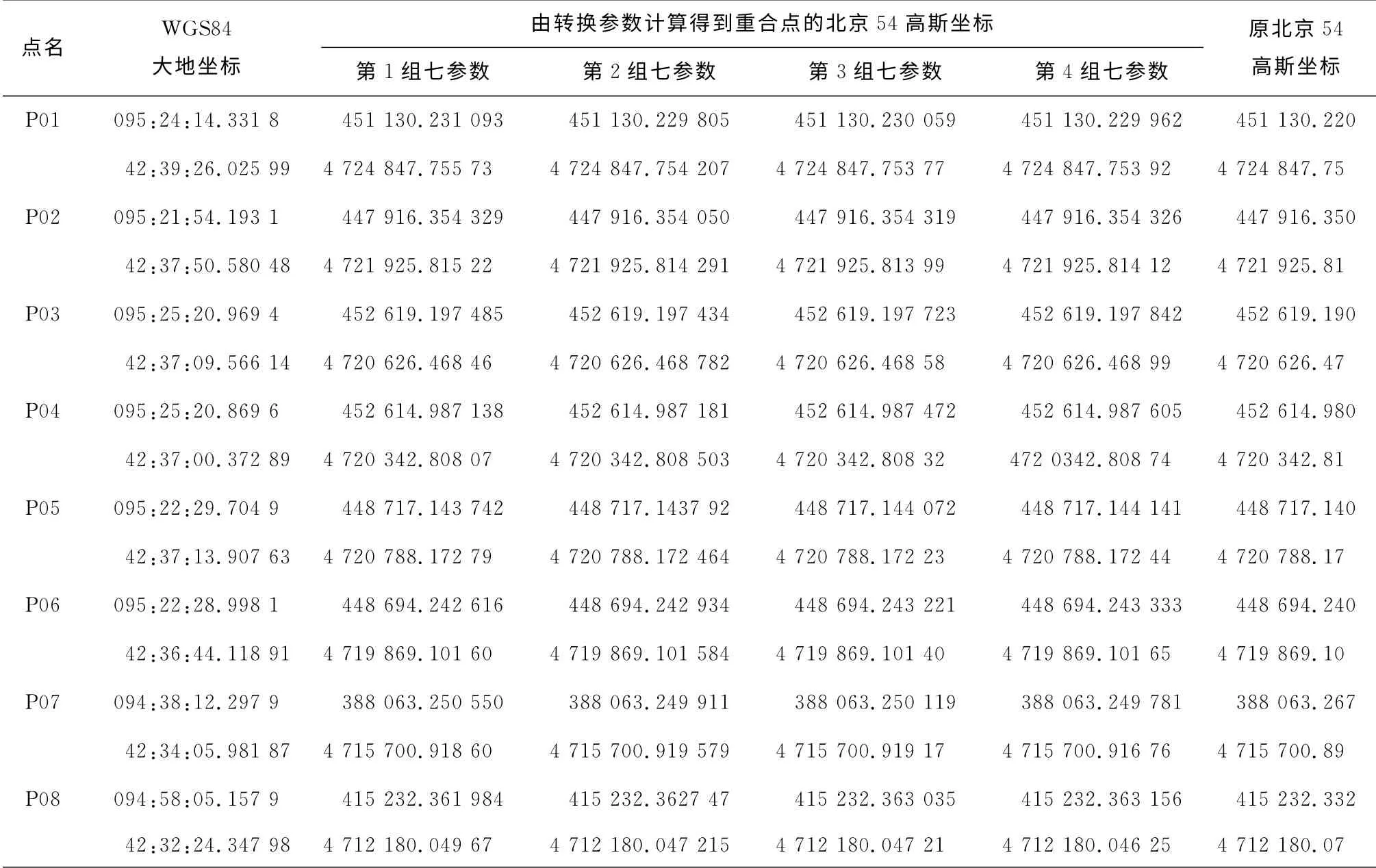
表2 重合点大地高误差对转换坐标的影响

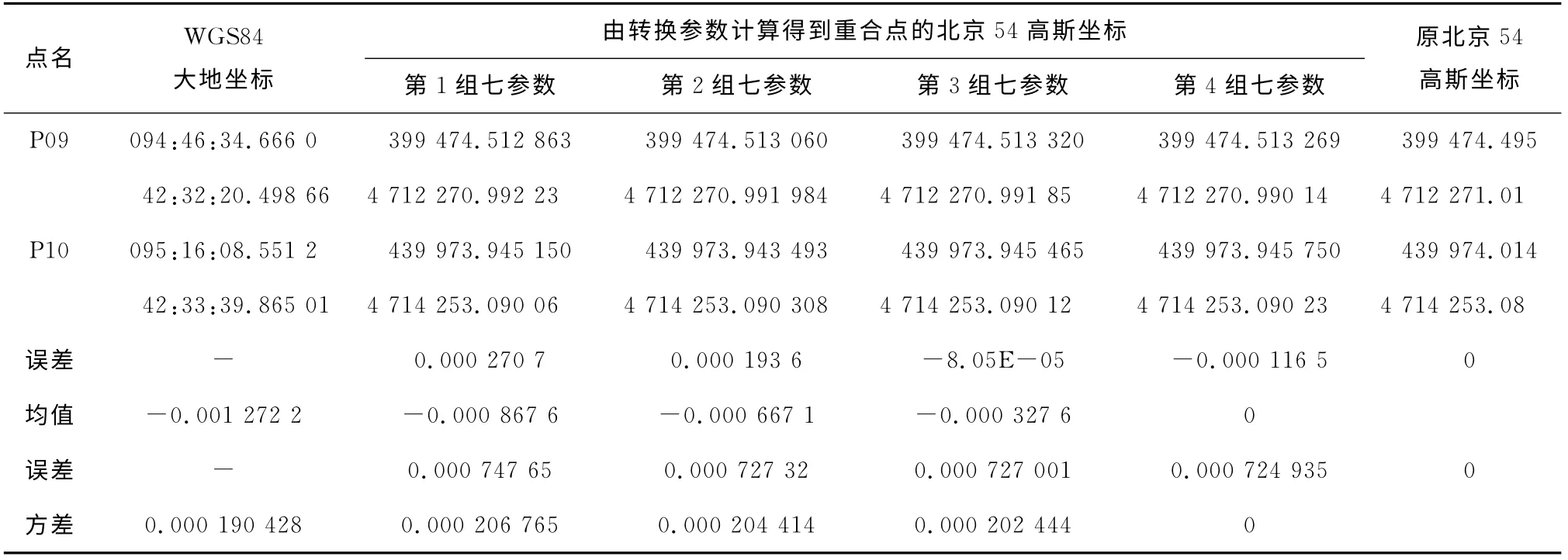
续表2

3 结 论

本文介绍了WGS84坐标系与本地坐标系的转换模型，分析了用局部椭球非大地高近似代替大地高时对转换参数、目标坐标的影响，最后通过实际算例证实了该影响的大小。

1）在局部范围内，用正常高或其他近似大地高求解的转换参数与理想值有差别，转换参数之间具有强相关性。

2）使用多组转换参数进行坐标系转换时，尽管转换参数有差别，转换得到的目标坐标的较差在厘米级，说明在局部范围内，用近似大地高引起的目标坐标误差很小，可以忽略。

［1］熊介.椭球大地测量学［M］.北京：解放军出版社，1988：311.

［2］王解先，王军，陆彩萍.WGS－84与北京54坐标的转换问题［J］.大地测量与地球动力学，2003，23（3）：70－73.

［3］施一民.现代大地控制测量［M］.2版.北京：测绘出版社，2008.

［4］施一民，陈伟，施宝湘.区域性独立坐标系与三维地心坐标系的转换［J］.同济大学学报：自然科学版，2009，37（8）：1104－1107.

［5］施一民，王丽华，周拥军.基于投影面由三维地心坐标系到区域性坐标系的转换［J］.同济大学学报：自然科学版，2011，39（1）：121－123.

［6］王解先，邱杨媛.高程误差对七参数转换的影响［J］.大地测量与地球动力学，2007，27（3）：25－28.

［7］朱华统.椭球大地计算［M］.北京：八一出版社，1993：16.