基于免棱镜全站仪的竖井高精度测量

曾怀恩，刘金平

（1.三峡大学 土木与建筑学院，湖北 宜昌 443002；2.三峡大学 三峡库区地质灾害教育部重点实验室，湖北 宜昌 443002；3.中交二航局第二工程有限公司，重庆 400042）

为了测试一种利用声音检测竖井（孔）三维形状的仪器（研制中）的准确可靠性，利用该声检测仪器与商用测量仪器测定同一口竖井的三维形状，通过两个三维形状的比对，进行分析和评价。声检测仪器测量精度较高，为了实现有效比对，要求测量仪器测定竖井的三维坐标在毫米级内。从测量速度和效率来看，三维激光扫描仪无疑是最佳的测量仪器选择，但是三维激光扫描仪昂贵，购置或租赁成本对于实验来说都难以承受。通过竖井现场踏勘以及考虑到实验经济性，最终选定的测量仪器为免棱镜全站仪。本文将就竖井测量中遇到的问题进行介绍，并提出相应的解决办法，实现基于免棱镜全站仪的竖井高精度测量。

1 竖井测量中的问题

需要测量的竖井位于某实验室内，其形状、尺寸如图1所示。图1中从上往下，井口半径为R1，R2，R3，越来越小，井底有近0.2m深的积水和少量淤泥。测量要求井壁凸凹变化越大的地方测量点越密，测量点的密度为相邻两点之间距离不超过8～10cm（竖井上部半径R1的柱面因较规则，测量点密度可放宽），以精确反映竖井三维形状，测量点位精度在毫米级内。实验时在井壁上测量点按网格挑选，相邻点距离满足测量要求，同时保证测量点的均匀性；测量仪器选用了三鼎STS－772R全站仪，其测角精度为2″；距离测量测程为免棱镜时350m，距离测量精度为免棱镜时5mm＋3ppm，在竖井测量几米范围内可以到达毫米级点位精度要求。

图1 竖井及3个基准点点位图

由于竖直角测量范围（约－45°～＋90°）的限制，若将全站仪安置在井口边缘地面，仪器高约1.5m，则井内可测量到的最低点距井口约1.5m，井最下端约2.5m高的范围内的点位不通视，无法测得，如图2所示。图2中为了描述方便，将不规则的井口径进行近似。为解决上述不通视问题，传统的竖井测量中，通常进行联系三角形测量将地面坐标和方位传递到井底，再进行井底测量［1－3］。为了回避繁琐的联系三角形测量，本文采用自由设站和再坐标转换的竖井测量方法。①将全站仪安置在井口边缘地面进行井上部分的测量，而且受视线的遮挡限制，一次安置仪器只能观测井壁约一半的范围，仪器下方井壁无法测量，所以至少要进行一次搬站；②将全站仪安置在井底进行井下部分的测量，视线对仰角无限制，但对俯角同样存在不小于－45°的限制，因此，要将仪器安置低一点（可将仪器投射激光调为常亮模式，操作仪器时不用眼睛瞄望远镜，直接瞄准激光点即可），尽量观测到井底深一些的点位，实际测量时，仪器高约1m，可测量井最低点距井底积水水面约0.4m。将仪器安置在井底时，因井底无控制点，也无法与井口边缘地面安置的仪器通视，只能进行自由设站。为了与地面上安置仪器测量坐标统一，特在井壁上方选了3个测量基准点，分别贴上了反射片，点位如图1所示，将全站仪安置在井口边缘地面、井底后，分别测定3个基准点在两套自由坐标系内的坐标，然后利用坐标转换方法将两套坐标统一。

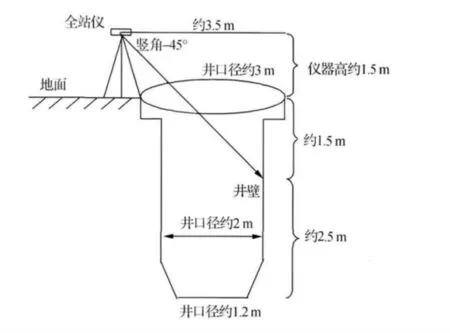
图2 竖井及3个基准点点位示意图

2 坐标、高程系统的统一

测量开始时，在井口边缘地面上选取一点并做了标记，将全站仪安置在该点上，假定该点北坐标、东坐标、高程均为0，通过罗盘确定正北方向进行定向，然后测量竖井上部半径R1的柱面上的可通视的点位，以及3个测量基准点；之后，将全站仪进行搬站，测量竖井上部半径R1的柱面上未测量到的点位；最后，将全站仪安置在井底，进行自由设站（假定设置点坐标、高程均为0），测量了井下部点位，包括3个测量基准点。获得的3个测量基准点的两套坐标见表1，表1中将地面、井底自由设站测量的坐标分别简称为地面坐标和井底坐标。

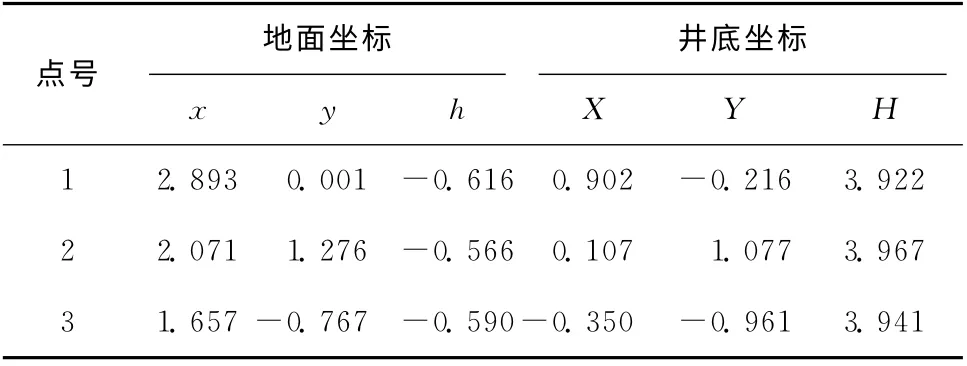
表1 基准点的两套坐标 m

由于测井区域较小，采用平面坐标相似转换法求解井底坐标到地面坐标的转换参数，转换数学模型为

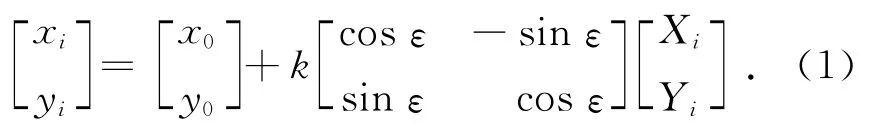
其中：i为点号，x0，y0为坐标平移参数，k为尺度因子，ε为旋转角，要求解该四参数，要求至少联测两个基准点。为了方便计算，令kcosε＝a，ksinε＝b，则式（1）改写成矩阵形式为

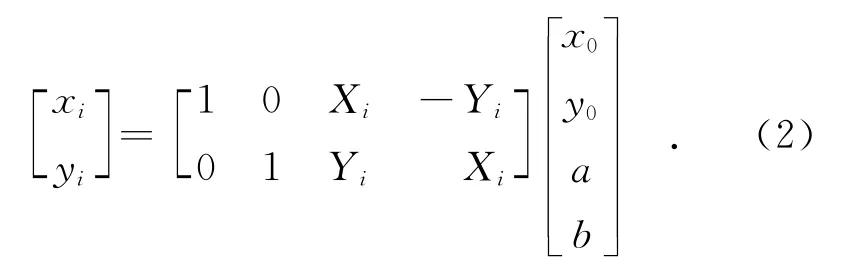
当基准点个数为n（n≥2）时，可建立2n个形如式（2）的方程，其最小二乘解为

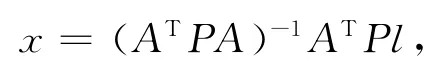
其中：

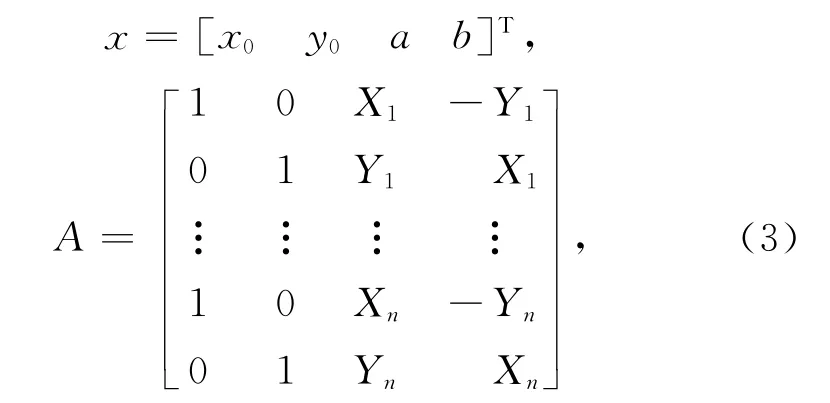
P为权阵，一般令P为单位矩阵，l＝［x1y1…xnyn］T。

为了检验坐标转换参数的可靠性，将基准点1、2坐标带入式（3）求解转换参数，再将基准点3的已知坐标与转换得到的坐标比对，评价转换精度。

解算得到的转换参数为：x0＝1.987 1，y0＝0.197 5，a＝0.999 214 801，b＝0.021 364 449，0.021 377 981rad，即ε为1°13′29.525 1″。解算中，注意到因自由设站获得坐标数值较小，A矩阵各元素量级相当，矩阵ATA条件数为4.8（较好），式（3）计算没有出现局域平面坐标变换中常见的病态性（一般可通过坐标重心化处理消除）［4－7］。将基准点3的井底坐标带入式（1）得到其地面坐标为［1.658，－0.770］，与 已 知 坐 标 较 差 为［0.001，－0.003］，即平面位置较差为0.003m。

由于测井范围很小，高程转换模型可取为

式中：Δh为高程转换参数，是一个常数，可由3个基准点分别算出Δh，再取均值作为最终结果。3个基准点分别算出高程转换参数为－4.538、－4.533、－4.531，三者最大较差为0.007m，可见高程测量精度较高，最终Δh取值为－45.534。从上述分析可知，竖井点位测量精度达到了毫米级。

3 竖井测量结果与分析

将井底坐标和高程通过式（3）和式（4）转换，可得到统一的地面坐标。测量共获得2 361个点位坐标和高程，利用MATLAB 7.1绘制竖井三维散点图，如图3所示，图中用十字叉符号表示测量基准点。利用MATLAB 7.1图形工具中的“旋转3D”可以直观查看竖井三维形状［8］。声检测仪器通过声测距原理也可测定竖井的三维形状，为了检测其测量精度，可与免棱镜全站仪测量竖井三维形状进行匹配分析，匹配基准可选用竖井中比较明显的特征点和线，如图3所示的两条突出线。

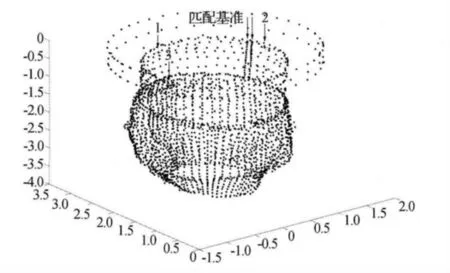
图3 竖井三维散点图

4 结束语

受测量仪器竖直角观测范围限制，井上边缘地面设站仪器与井底存在不通视的问题，测量中通常采用联系三角形测量将地面坐标和方位传递到井底，再进行井底测量。本文不采用联系三角形测量，而进行井上地面及井下自由设站测量。为了将两次自由设站测量坐标统一，测量中联测井口3个基准点，然后利用基准点坐标、高程求得两套坐标、高程转换参数，实现两套坐标、高程之间的转换。这种竖井测量方法避开了繁琐的联系三角形测量工作，提高了测量效率，为竖井测量提出了一种新思路。利用高精度测量数据，绘制竖井三维散点图，为测试声检测仪器检测竖井三维形状准确可靠提供标准模型，达到良好效果。

［1］罗三明，万文妮，高培芝，等.盾构工程竖井联系测量数据处理方法研究［J］.大地测量与地球动力学，2007，27（5）：123－127.

［2］姬晓旭，刘成龙，何波.竖井联系测量的新方法及其应用［J］.铁道勘察，2009（5）：14－17.

［3］陈方敏.吊钢丝联系三角形法在隧道测量大型深竖井定向中的应用［J］.城市勘测，2010（2）：135－137.

［4］姚宜斌.平面坐标系统相互转换的一种简便算法［J］.测绘信息与工程，2001（1）：1－3.

［5］刘陶胜，黄声享，罗力，等.基于重心基准的平面坐标转换研究［J］.大地测量与地球动力学，2011，31（2）：102－106.

［6］曾怀恩，黄声享.三维坐标转换参数求解的一种直接搜索法［J］.武汉大学学报：信息科学版，2008，33（11）：1118－1121.

［7］Huaien Zeng，Qinglin Yi.Quaternion－based iterative solution of three－dimensional coordinate transformation problem［J］.Journal of Computers，2011，6（7）：1361－1368.

［8］周开利.Matlab基础及其应用教程［M］.北京：北京大学出版社，2007.