GNSS在线数据处理系统在工程控制网中的应用与分析

畅 毅，畅 鑫，陈信华

（1.中国石油集团东方公司装备服务处长庆作业部，宁夏 银川 750006；2.武汉大学 测绘学院，湖北 武汉 430079；3.福建信息职业技术学院，福建 福州 350007）

随着计算机技术、GNSS技术和国际互联网等技术的联合应用和发展，尤其是基于网络的GNSS定位技术和数据处理方法的不断完善，各种网络GNSS在线数据处理系统如雨后春笋般的发展起来。用户不论在世界上的任何地方，只要按要求将观测数据及相关信息通过在线提交或者电子邮件的方式提交给GNSS在线数据处理系统，就可以在电子邮箱中收到数据处理结果，这样不仅给GNSS用户带来了方便，而且还提高了作业质量并降低了作业成本。

目前，主要的GNSS在线处理系统有7个，详见表1。由于各个系统的设计理念、解决问题的侧重面不同，如：AUSPOS（V2.00）、SOPAC－SCOUT、OPUS等系统都是采用自动下载上传站点附近的3个点（含3个点）以上的IGS或CORS参考站参与计算和网平差的解算方式进行定位计算的；而CSRS－PPP、APPS、GAPS和magicGNSS系统则是采用基于非差技术的精密单点定位的解算方式进行定位解算的。在系统的稳定性、可操作性、适宜条件及数据处理结果的精度和可靠性等方面，已经有不少学者在报告或论文中进行了深入的探讨，也给出了相关的结论，但这些报告或论文基本上都是基于固定台站数据来进行数据处理与分析的。本文主要结合某测区的GNSS工程控制网的实际数据，来探讨GNSS在线数据处理系统在工程控制网中的适宜性和精度分析，为用户在工程控制网中应用GNSS在线数据处理系统提供探讨和服务。

表1 7个主要GNSS在线处理系统及网址

1 工程控制网及GNSS在线数据处理系统的主要特点

1.1 工程控制网简介

鄂尔多斯苏里格南国际合作区GPS控制网共布设了13个高精度控制点，数据采样间隔为15s，接收机为Leica 1230。网中每个点最短的观测时间约为2×23h50m；点间距最大为278km，平均距离为56km；其中：CS16、GT12、GS55、G166均为2000国家大地坐标系成果点，3084、3643、3233、2993、3106、3161为新布设的控制点，SuMu、HuBa、YC01为国家1954年北京坐标系成果点，详见图1。

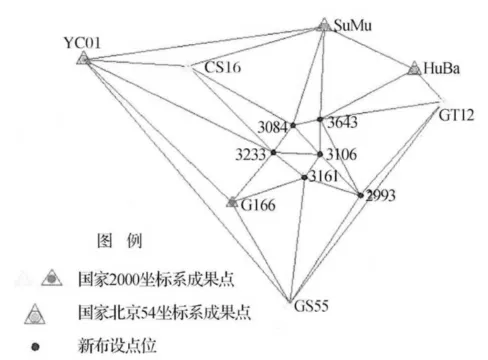
图1 鄂尔多斯苏里格南国际合作区GPS控制网

1.2 GNSS在线数据处理系统的主要特点

本 文 采 用 了AUSPOS V2.00、SOPACSCOUT、OPUS、CSRS－PPP及APPS等5个常用GNSS在线数据处理系统，它们的特点［1－4］如下：

1）它们都是免费使用的，AUSPOS（V2.00）、SOPAC－SCOUT及OPUS都无需注册，而CSRSPPP及APPS需要免费注册；

2）SOPAC－SCOUT是 采 用GAMIT/GLOBK后台处理，对用户的观测数据质量要求比较高，APPS同样对用户的观测数据质量要求比较高。

2 GNSS在线数据处理结果精度与分析

2.1 数据与数据处理比较方案选取

1）根据鄂尔多斯苏里格南国际合作区GPS控制网的基本情况，选取了有已知成果（CS16、G166、GT12、GS55）和有平差成果的点（2993）参与数据处理与对比分析；

2）利用TEQC工具软件将这些点的每个23h50m观测数据分割为1h、1.5h、2h、2.5h、3h、3.5h、4h、4.5h、5h、5.5h、6h、7h、…、23h、23h50m等不同观测时间长度的数据，采用不同的系统分别处理，利用每个观测点多日观测值数据处理结果的平均值与每个观测时段长度数据处理结果进行比较，分析五大系统的解算精度随观测数据时段长度的变化规律，验证其内符合精度；

3）将各个系统解算的结果与已知的2000国家大地坐标系成果或用2000国家大地坐标系成果约束下的网平差成果比较，验证各个系统的外符合精度。

2.2 数据处理结果精度与分析

方案1：图2～6分别给出了用APPS、AUSPOS（V2.00）、CSRS－PPP、OPUS及SCOUT解 算 的CS16观测点不同数据量的解算坐标与3d23h50m解算坐标平均值的差值。分析各图可见：

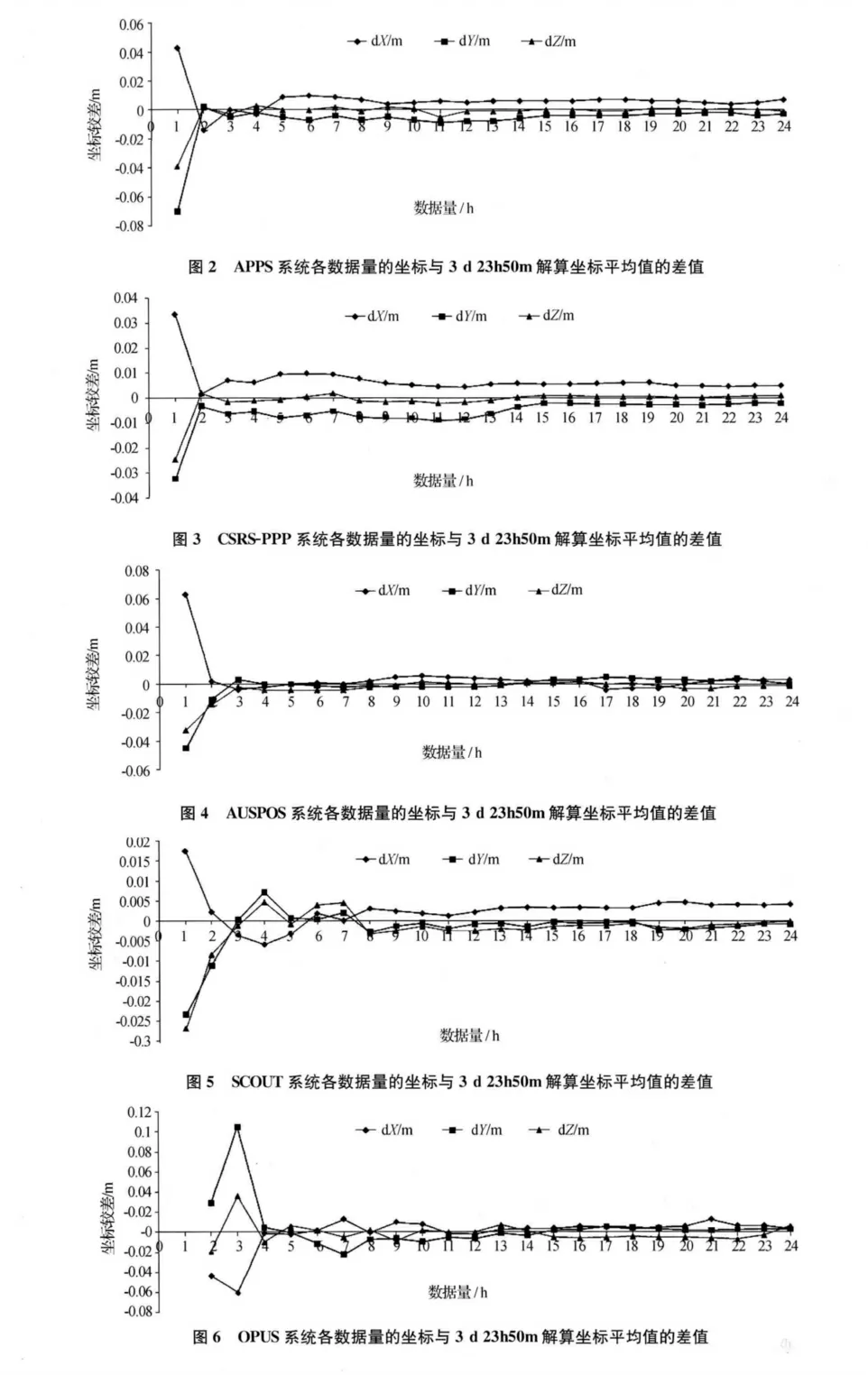
1）各个系统3d23h50m解算坐标的平均值与不同数据量的解算坐标的差值都随数据量的增加而趋于平稳，AUSPOS（V2.00）和SCOUT系统的差值最小；而OPUS系统的差值相对较大，基本在2cm。

2）从图2、图3可以看出：APPS及CSRS－PPP系统3h后3个坐标分量的差值基本都在10mm以内，其内符合精度较好。

3）从图4、图5可以看出：AUSPOS（V2.00）系统3h后3个坐标分量的差值基本在5mm以内；SCOUT系统5h后3个坐标分量的差值基本在5mm以内；其内符合精度最好。

4）从图6可以看出：OPUS系统4h后3个坐标分量的差值基本都在20mm以内，其内符合精度一般。

方案2：选取具有2000国家坐标系（CGCS2000）坐标的CS16、GT12、GS55、G166 4个点各个系统与其坐标真值进行比较，表2给出了五大GNSS在线处理系统处理的多天平均值与真值的比较（为便于统计对比，表中数据只取小数点前一位及其尾数的部分进行比较，下同），其中：△X最大为0.336 4m，最小达0.301 5m；△Y最大为－0.155 3m，最 小 为0.053 7m；△Z最 大 为0.155 4m，最小为0.088 0m。

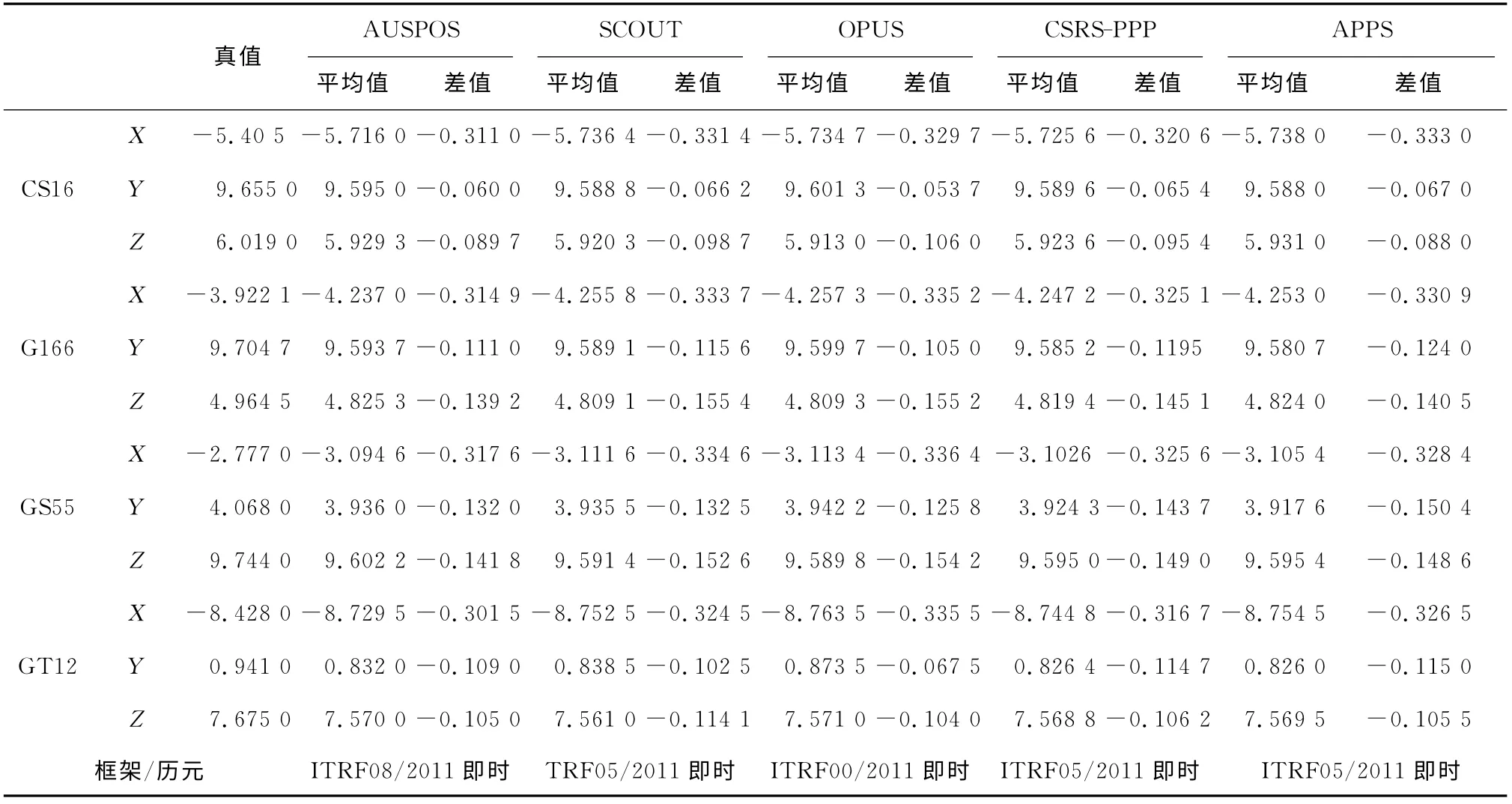
表2 五大GNSS在线处理系统处理的多天平均值与真值的比较 m

虽然表2给出的各个系统处理的多天平均值与其坐标真值的差距较大，但不能简单地判定其外符合精度不好。因2000国家坐标系（CGCS2000）采用的是ITRF97框 架2000.0历 元［5－6］，而 各 个 系 统数据处理结果都是基于表2最后一行所给出的框架和历元，由于地球表面上一点的坐标受板块运动和潮汐影响在时间上和空间上是变化的［7］，所以就导致了不同框架、不同历元下的同一个站点的坐标差异较大，为便于实用，必须将其结果转换到基于ITRF97框架2000.0历元下的坐标，必须进行框架和历元的转换，进一步检核其外符合精度。

3 坐标转换及精度分析

要把基于参考框架为ITRF XX、指定历元的观测数据转换到ITRF97框架、2000.0历元下的CGCS2000坐标系统有3种转换方式［5］：①按已公布的ITRF框架之间的转换关系进行转换；②通过公共点求解转换参数进行坐标转换；③通过平差的方法将GPS网纳入到2000国家大地坐标系。

3.1 坐标转换

1）按照方法1进行ITRF框架之间的转换时，2个ITRF框架下的X，Y，Z坐标的转换参数必须已知，一般不好实现。在没有直接的转换关系的情况下，可将ITRFXX框架作为过渡实施转换。在ITRF框架固定的前提下，控制点在不同历元下对应的坐标也是不同的，通过转换公式将同一框架下不同参考历元的控制点坐标转换为同一参考历元下的坐标成果［5，8－9］。

通 过 式（1）分 别 将ITRF2008、ITRF2005、ITRF2000框架下的2011即时历元的待处理坐标转换为2000.0历元坐标成果。

将参考历元t1转换为t2的转换公式为

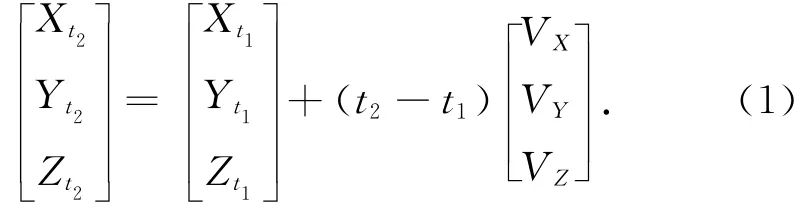
式中：t1为原参考历元，t2为需转换到的参考历元，［Xt1，Yt1，Zt1］T为原参考历元下控制点坐标，［Xt2，Yt2，Zt2］T为需转换到的参考历元的控制点坐标，［VX，VY，VZ］T为控制点的速率。原参考历元下控制点坐标及速率，可以从ITRF网站（http://itrf.ensg.ign.fr/ITRF）所提供的相应的框架站点坐标文件获取。

再利用式（2）布尔萨·沃尔夫模型及CS16、GS55、GT12、G166 4个公共点中的3个（CS16、GS55、GT12）分别求取的ITRF2008、ITRF2005、ITRF2000框架下的2000.0历元的坐标到ITRF97框架下的2000.0历元的坐标的转换参数，依其不同的转换参数分别进行坐标转换（方法2），G166点作为检核点，根据计算参数进行坐标转换后的坐标值与真值较差来检验各系统外符合精度，详见表3。

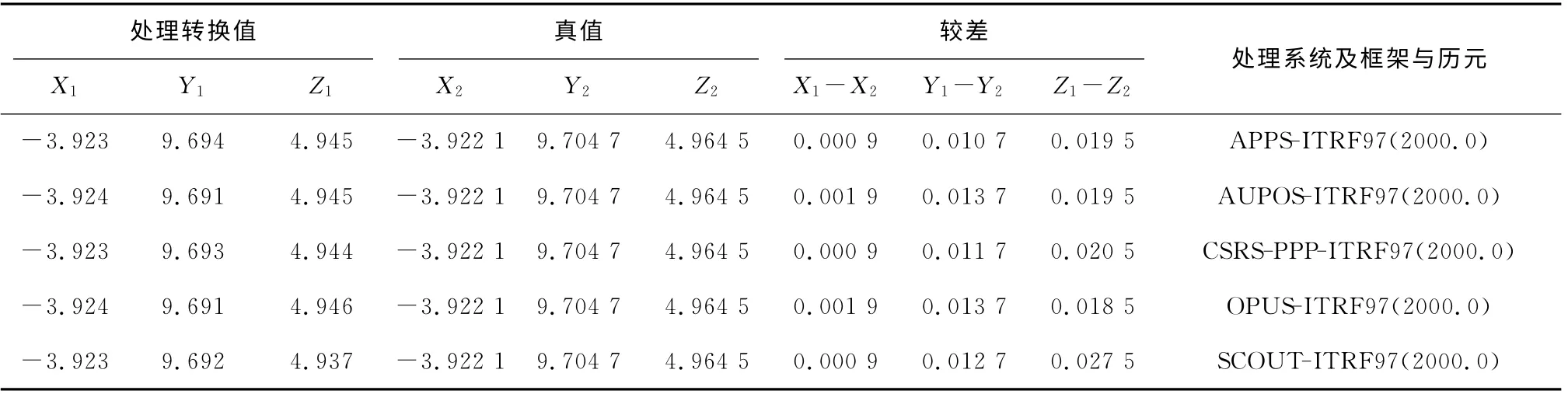
表3 G166点各系统数据处理结果转换值与真值比较m

布尔萨·沃尔夫模型又称为七参数转换或七参数赫尔模特变换，在该模型中共采用了7个参数，分别是3个平移参数、3个旋转参数（也被称为3个欧拉角）和1个尺度参数m。设有2个分别基于不同基准的空间直角坐标系，OA－XAYAZA和Ob－XBYBZB，采用布尔沙模型将OA－XAYAZA下坐标转换为Ob－XBYBZB的坐标转换公式为

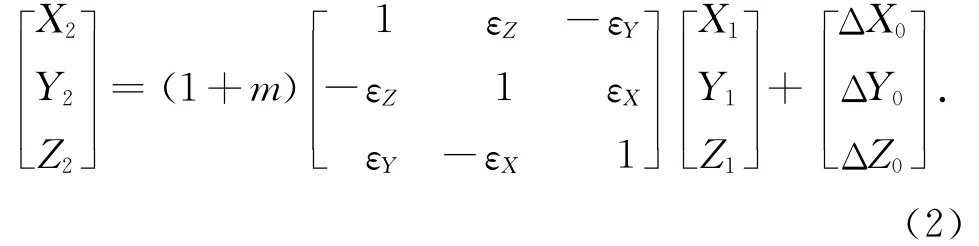
式中：ΔX0、ΔY0、ΔZ0为3个平移参数，εX、εY、εZ为3个旋转参数，m为尺度变化因子［8］。

2）鄂尔多斯苏里格南国际合作区GPS控制网观测数据是采用Leica 1230随机软件LGO 7.0加精密星历处理的，网平差则是选取CS16、GS55、GT12、G166 4个具有2000国家大地坐标系坐标的点，约束其CS16、GS55、GT12 3点的坐标进行平差，求取网中其它点的2000国家大地坐标系坐标（平差值），G166点作为检核点，根据平差后的坐标值与真值较差来检验工程控制网的外符合精度，见表4、表5。

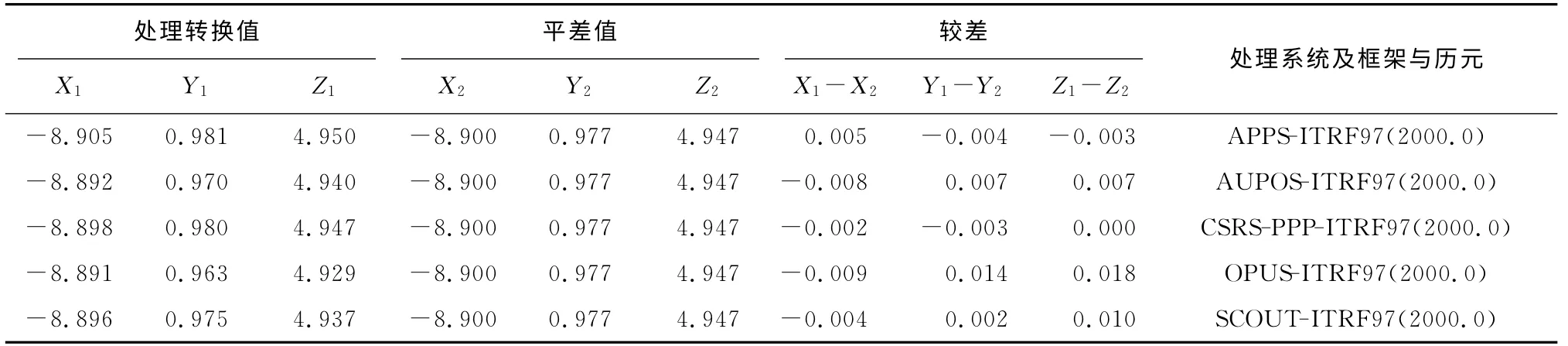
表4 2993点各系统数据处理结果转换值与平差值比较m

表5 G166点平差值与真值比较 m

3.2 精度分析

1）经过将ITRF2008、ITRF2005、ITRF2000框架下的历元转换及相同历元下的不同框架的转换，所得的G166点各系统数据处理结果转换值与真值比较，X，Y，Z坐标差值最大为2.75cm，最小为0.9mm，符合精度很好；

2）经过将ITRF2008、ITRF2005、ITRF2000框架下的历元转换及相同历元下的不同框架的转换，所得的2993点各系统数据处理结果转换值与平差值比较，X，Y，Z坐标差值最大为1.8cm，最小为1.0mm，符合精度也很好；

3）经过基于2000国家大地坐标系，约束其CS16、GS55、GT12 3点的坐标进行平差，所得的G166点的平差值与真值比较，X，Y，Z坐标差依次为：0.1mm、0.3mm和0.5mm，符合精度更好。

4 结 论

1）本文所用到的5个GNSS在线数据处理系统，不论是以观测点附近的3个点（含3个点）以上的IGS或CORS参考站参与计算和网平差解算方式进行定位计算的系统，还是基于非差技术的精密单点定位解算方式进行定位解算系统，其性能都很稳定、方便和快捷，只需用户按一定要求上传数据，就可获得准确的处理结果，除APPS以外的系统都支持网页提交数据，界面友好，交互性强；

2）对于以观测点附近的3个点（含3个点）以上的IGS或CORS参考站参与计算和网平差解算方式进行定位计算的AUSPOS（V2.00）、SOPACSCOUT、OPUS等系统，尽管本文分析指出观测数据大于4h就可得到厘米级的定位精度，但实际上由于目前国内能参与计算或能提供转换所需的精准坐标及速度的IGS或CORS站不多且分布不均，甚至距观测点都在数百千米以外，所以，建议观测时间最好选6h以上，以获得稳定可靠的成果；

3）对基于非差技术的精密单点定位解算方式进行定位解算的CSRS－PPP、APPS等系统，因数据处理过程中要探测和剔除带有误差的数据，求得“干净”的数据参与计算，所以，建议观测时间最好选6h以上，以获得稳定可靠的成果；

4）鉴于各个系统的优越性，只要数据观测量足够，对于任何工程控制网，用户都可放心使用本文介绍的任一系统或几个系统处理数据，这样既可以减少作业人员的劳动强度，又节约作业成本。

5）由于受地球上板块运动和潮汐影响在时间和空间上的变化，加之坐标系统间的差异，建议在实际工作中一定要顾及位置和时间的变化，将框架和历元归算到统一规定的系统下使用。

［1］徐莹，聂桂根，吕乔森.GNSS在线数据处理系统的比较与分析［J］.测绘通报，2010（12）：30－33.

［2］金蕾，胡友健，梁新美.GPS在线数据处理软件的精度分析［J］.地理空间信息，2007（2）：85－87.

［3］李黎，戴吾姣，李浩军，等.AUSPOS在线定位系统研究分析［J］.全球定位系统，2008，33（5）：43－46.

［4］牛作鹏，张书华，张丽.APPS定位服务系统精度分析［J］.测绘信息与工程，2010，35（5）：20－21.

［5］程鹏飞，成英燕，文汉江，等.2000国家大地坐标系实用宝典［M］.北京：测绘出版社，2008.

［6］党亚民，成英燕，薛树强.大地坐标系统及其应用［M］.北京：测绘出版社，2010.

［7］魏子卿.2000中国大地坐标系及其与WGS84的比较［J］.大地测量与地球动力学，2008（10）：1－5.

［8］林晓静，张小红，郭斐.ITRF2005与CGCS2000坐标转换方法与精度分析［J］.大地测量与地球动力学，2010，30（2）：117－119.

［9］［奥］霍夫曼－韦伦霍夫，利希特内格尔，瓦斯勒.全球卫星导航系统GPS，GLONASS，Galileo及其他系统［M］.程鹏飞，蔡燕辉，文汉江，等译.北京：测绘出版社，2009.