一种改进的BP神经网络非均匀性校正算法

林 斌，范永弘

（信息工程大学 测绘学院，河南 郑州 450052）

对于理想的红外焦平面阵列，有相同的入射辐射就该有一致的响应输出。但是在实际过程中由于材料质量和制作工艺等因素的影响，每个探测器在阻抗、容抗、热敏面积、电阻温度等方面都存在微小差别，使得实际响应输出并不一致，这就是IRFPA响应的非均匀性［1］。非均匀性的直接结果就是使红外图像产生不同程度的噪声，影响成像质量，这种情况下就要对红外焦平面阵列进行非均匀校正［2］。红外图像的非均匀性校正方法很多，但是总的来讲分为两大类：第一类是基于定标技术的，第二类是基于场景技术的［3］。基于定标技术的算法主要应用于噪声不变的非均匀校正中，但是在实际过程中却不能避免噪声漂移带来的问题，因此需要一种能够解决这一问题的算法，即基于场景技术的非均匀校正算法。

传统神经网络校正法是基于场景技术的非均匀校正方法，由于它是一个反馈模型，根据误差调整阈值和权值，所以在理论上它完全不需要对IFPRA进行定标，对探测器参数的线性和稳定性要求也不高，但是其存在收敛速度慢［4］、校正精度低、边缘模糊和迭代步长不易选择等缺点。基于这些问题，文献［5］提出了利用BP神经网络进行非均匀校正，而且选用不同的步长达到快速收敛的效果。此算法效果良好，但是图像容易出现边缘模糊。本文在其基础上进行改进，提出基于中值滤波和添加动量项的BP神经网络非均匀校正算法。结果表明，改进的算法可以有效保留图像边缘细节。

1 BP神经网络

人工神经网络是在精神病学家和神经解剖学家McCulloch与数学家Pitts于1943年提出的神经元生物学模型基础上发展起来的模拟人脑信息处理的人工智能技术［6］。人工神经网络集合了大量简单神经元，并将其进行互联组成一个复杂网络，因此，它是一种典型的多元输入、单元输出模型。其数学模型为

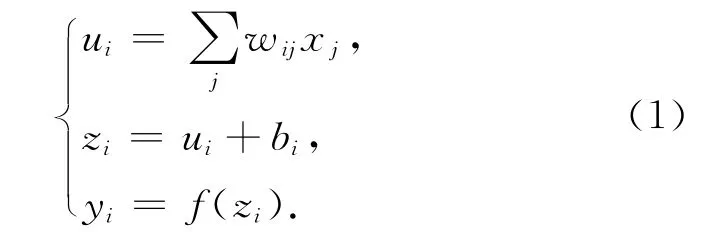
式中：w为输入值与神经元连接的权值，x为网络的输入值，b为阈值，u为神经元的净输入值，z为调整后的值，同时称为神经元的局部感应区，f（.）为激励函数。

BP神经网络是一种多层次前馈神经网络，该网络的主要特点是信号前向传递，误差反向传递。在前者传递中，输入信号从输入层经隐含层逐层处理，直至输出层，每一层的神经元状态值影响下一层神经元状态。如果输出层得不到期望输出，则转向反向传播，根据预测误差调整网络权值和阈值，从而使BP神经网络预测输出不断逼近期望输出。BP神经网络的拓扑结构如图1所示。

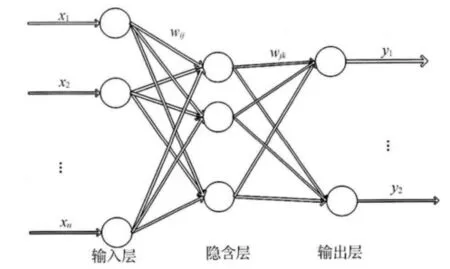
图1 BP神经网络

根据图1，在某种程度上可以把BP神经网络比作一个非线性函数，该函数的自变量和因变量即是网络的输入值和预测值。利用非线性可微分函数进行权值训练，具有自适应、自学习能力，在自动控制、飞行轨道模拟、噪声抑制、模式识别等众多领域得到了广泛的应用。

2 BP神经网络非均匀性校正算法

［5］可以得到BP神经网络算法进行焦平面阵列非均匀性的具体实现形式。此算法包含输入层、隐含层和输出层三层网络结构，其中有5个输入、3个隐含层输入、1个输出。网络输入值是探测元D（i，j）及其相邻上下左右探测元第n帧的图像输出，用X（n）表示。输入层X和隐含层yi之间的权值矩阵及其阈值用Wi（n），bi（n）表示，隐含层和输出层之间的权值矩阵和阈值用Vn，bn表示。隐含层的激励函数为

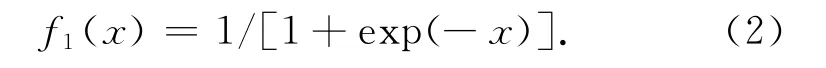
输出层的激励函数是f2（x）＝x。

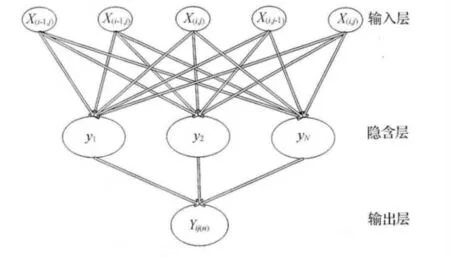
图2 BP神经网络非均匀校正网络结构

探测元（i，j）第n帧的期望输出为其相邻4个探测元的平均值，误差函数分别为

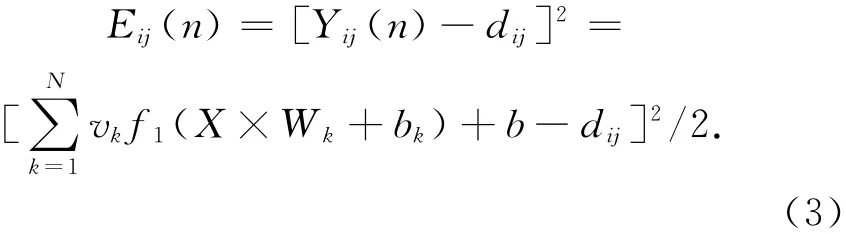
控制量根据梯度修正法修正权值和阈值，使得不断接近期望值。

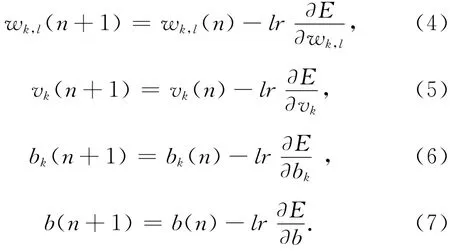
式中lr为学习速率。通过反复迭代，最终得出逼近的期望值。

3 基于中值滤波和改进权值的BP神经网络校正算法

3.1 中值滤波预处理

在较弱的空间噪声下，神经网络算法具有较好的校正效果；但是在较强的空间噪声下，该算法的校正效果较差。因此控制强噪声是发挥神经网络校正算法性能好坏的直接因素之一。由于中值滤波器在消除椒盐噪声和保护图像细节方面具有良好的效果，所以本文采用了中值滤波器对红外图像的噪声进行预处理。中值滤波器的表达式为

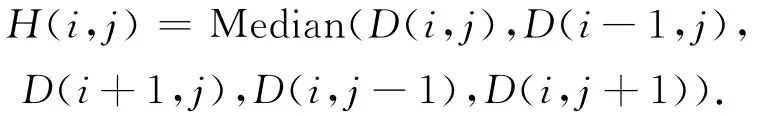
该中值滤波器实现了将像元D（i，j）及其四邻域的输出值进行中值处理，最后将处理后的输出值H（i，j）作为D（i，j）的值。

3.2 添加动量项的BP神经网络校正算法

对文献［5］提出的BP神经网络算法进行改进，主要在以下两方面：

1）对中值滤波后的图像灰度值进行归一化处理。

2）采用增加动量项的方法提高学习效率，防止陷入局部最优产生边缘模糊。

数据归一化是指神经网络在进行结果预测前对输入数据的一种处理方法，其目的就是将输入数据都转换到［－1，1］，这样可以避免各维数间因数量级差别而造成网络预测误差增大的情况发生。

上节中神经网络权值迭代采用梯度学习算法，网络权值修正较慢且容易陷入局部最优，故本文采用了通过增加动量项的方法提高网络学习效率。增加动量项的权值和阈值学习公式为

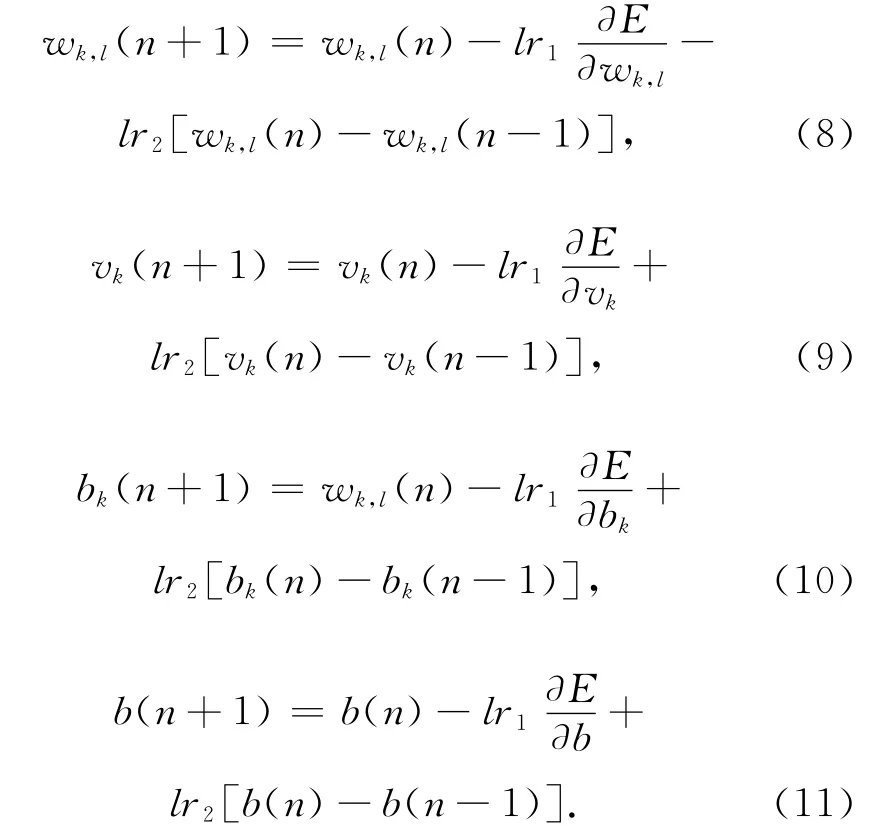
式中：lr1，lr2为学习速率。通过式（8）～式（11）对权值和阈值进行迭代，可以改善局部最优。

4 BP神经网络算法的仿真

本文选用128＊128的模拟红外焦平面阵列响应图像作为实验仿真图，并采用matlab进行算法的仿真。图3（a）表示红外焦平面理论输出图像，图3（b）表示噪声强度很大的图像。

图3 焦平面理想图像和含有非均匀性的图像

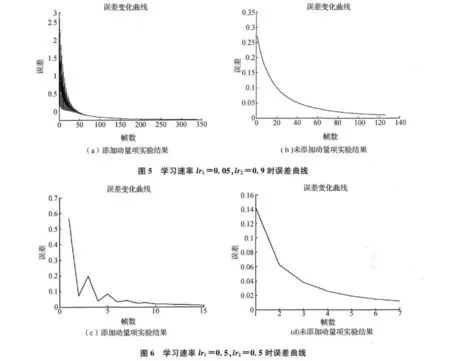
首先对图像采用中值滤波器进行预处理，然后利用matlab进行BP神经网络非均匀校正实验仿真。该BP神经网络采用5个输入、3个隐含层和1个输出的模型。图4表示实验结果，其中图4（a）表示采用上述中值滤波器进行中值滤波的的实验图；图4（b）表示在图4（a）的基础上进行BP神经网络运算的实验结果（epoch＝200）。最后随机选取一个探测元D（i，j），将其输出以及相邻的上下左右4个探测元的输出作为BP神经网络的输入，在原来和改进算法上进行实验验证，并选用不同的学习速率分别进行仿真。图5和图6分别表示在不同的学习速率下未添加动量项时的误差曲线和添加动量后的误差曲线。

图4 实验仿真结果

从实验结果看，经过中值滤波器进行中值滤波预处理后，图像（图4（a））已明显去除了大量噪声，再采用添加动量项的BP神经网络进行图像的非均匀校正，图像在第200帧的结果如图4（b）所示。从实验结果看，图像在预处理后的基础上非均匀性校正效果明显，而且图像的边缘细节保留较好。从图5和图6的误差曲线走势看，当采用较大的学习速率时（Lr1＝0.5，Lr2＝0.5），网络的收敛速度快（见图6）。当设定期望输出与随机选取探测元输出值的均方误差为1%时，未添加动量项的BP神经网络方法比添加动量项的速度提高一倍。同样设定均方误差为1%，当采用较小的学习速率时，发现两者的收敛速度都变慢，尤其以添加动量项的更为显著。

5 结束语

根据以上的实验分析可知，对于本文提出的添加动量项的BP神经网络算法，在非均匀性很大的情况下，可以先采用中值滤波器进行图像预处理，这样可以去除一些椒盐噪声而且能够保留一些图形细节，然后可以根据图像的边缘细节情况选用是否添加动量项。若图像边缘细节丰富，则选用添加动量项的BP神经网络，并选用较小的学习速率，虽然耗费的时间长一点，但这样可以保证图像较好的保留边缘细节；相反，则选取未添加动量项的BP神经网络方法。

参考文献：

［1］常本康，蔡毅.红外成像阵列与系统［M］.修订版.北京：科学出版社，2006：229.

［2］吴传玺，代少升.基于中值滤波的红外焦平面阵列非均匀性神经网络校正［J］.红外，2010，31（8）：14－18.

［3］Xing Su－xia，Zhang Jun－Jv，et al.Two－point Nonuniformity Correction based on LMS［J］.SPIE，2005，5640：130－136.

［4］张科，赵桂芳，崔瑞青，等.神经网络非均匀性校正算法中初始权值选取方法［J］.激光与红外，2007，37（3）：248－251.

［5］朱杰，麻芃，宋利权，等.焦平面阵列BP神经网络非均匀性校正及其算法改进［J］.红外技术，2010，32（7）：377－380.

［6］Scribner D A，Sarkady K A，Gaulfield J T，et al.Nonuniformity correction for stating IR focal plane arrays using scene－based techniques［C］//Proceddings of SPIE，Infrared Detectors and Focal Plane Arrays，1990，1308：224－233.

［7］楼波，张峰，宋利权，等.改进的神经网络非均匀性校正方法［J］.红外与激光工程，2008，37（2）：300－303.