半参数模型精度研究

黄 凯

（上海市测绘院，上海，200063）

在测量数据处理中，常常要对一系列观测数据进行分析研究，这些数据通常与时间有很强的关联性，通常称它们为“动态数据”或“时间序列”。在时间序列分析中，通常假定观测误差只含有偶然误差，不含系统误差，而在实际观测数据中一般含有系统误差。测量数据处理建立的动态处理模型中AR（p）模型、MA（q）模型、ARMA（p，q）模型等都是假定观测值没有系统误差时建立的模型，存在模型误差。

半参数回归分析模型是一种既含有参数分量又含有非参数分量，本文将半参数回归分析方法引入AR（p）模型，建立适于测量数据处理的理论与方法，在确定未知参数的同时能将模型误差与偶然误差分离开来，并对半参数模型的引入对精度的影响进行比较研究。

1 时间序列

时间序列［1］的定义，由一串随机变量…，x1，x2，x3，…构成的序列叫做随机序列，用xt（t＝…，1，2，3，…）或｛xt｝表示。如果下标t是整数变量，它代表着间隔的时刻增长量，而整数变量t即认为是指某时刻。建立时序模型的基本思想是认为同一变量在现在时刻的观测值，在时间上同以前的观测值是有联系的，当然在新的时刻会出现未预料的新情况。因此，若记xt（t＝…，－2，－1，0，1，2，…）是一个时间上无限伸展的序列，则可提出一种描述该序列的模型是xt＝f（xt－1，xt－2，…）＋at，这里的函数f把现在的情况同以前的情况联系起来，而at表示时刻t出现的新情况，假定它是同t时前的情况无关的随机因素。模型主要包括：

1.1 自回归（AR）模型

时间序列模型中只有有限项模型xt＝φ1xt－1＋φ2xt－2＋…＋φpxt－p＋a1，称为自回归（Autoregressive）模型，其中p为自回归的阶，φ1，φ2，…，φp为自回归系数，at是均值为0、方差为σ2a的正态分布白噪声，即at－NID（0，σ2a），符号NID表示独立正态分布。这样的模型记为AR（p）。

1.2 滑动（MA）平均模型［2］

时间序列模型中只有有限项的模型xt＝atθ1at－1－…－θqat－q称为滑动（Moving Average）平均模型。这里q为模型的阶次；θ1，θ2，…，θq为滑动平均系数；at是白噪声序列，其平均值为0，方差为σ2a。这样的模型记为MA（q）。

1.3 自回归滑动平均（ARMA）模型

为了使模型在拟合实际数据时具有更大的灵活性，有时在模型中既包含自回归部分也包括滑动平均部分，这就是自回归滑动平均模型。其表达式为xt－φ1xt－1－…－φpxt－p＝at－θ1at－1－…－θqat－q简记为ARMA（p，q）。其中p和q分别是自回归部分和滑动平均部分的阶数，φi（i＝1，2，3，…，p）和θi（i＝1，2，3，…，q）分别是自回归系数和滑动平均系数。

2 半参数的引入与建模求解

2.1 半参数的引入

在测量数据处理中，通常假定观测误差只含有偶然误差，不含系统误差和粗差。观测真值可表示为一组参数的线性函数，在这种情况下，称观测值已被完全参数化，但实际上观测值很难被完全参数化。首先，影响观测值取值的因素很多，建立数学模型时往往无法考虑到所有的这些因素。其次，观测值与参数之间的函数关系可能比较复杂，为了处理方便，经常选择较为简单的函数关系来代替。因此，平差时建立的函数模型只是实际问题的近似表达，也就是说存在模型误差。当模型误差与偶然误差相比是一个微小量时，忽略模型误差不会对参数估计值产生太大的影响，而当模型误差比较大时，就会对参数估计产生较大的影响，甚至会导致错误的结论。

上述问题得不到很好解决的主要原因在于没有找到一个合适的数学模型来描述残差的模型误差或观测值中的系统误差。用半参数回归分析模型既含有参数分量又含有非参数分量，用它描述实际问题时，更能充分地利用观测值所提供的信息。将半参数回归分析方法引入AR（p）模型，建立适于测量数据处理的理论与方法，在确定未知参数的同时能将模型误差与偶然误差分离开来，从而使这一问题得到解决。

2.2 半参数模型及解算方法

AR（p）模型［3］为

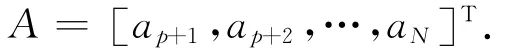
在此模型中，通常假定A是期望为0的偶然误差。也就是说除去观测误差，观测值xi完全表示为参数φ的函数。如果模型不准确，或观测值中有系统误差，式（1）并不能严格成立，而改写为

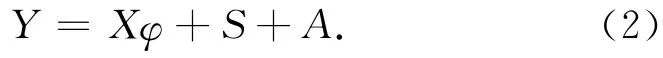
式中：S＝［s1，s2，…，sN－1－p］T是一个描述模型误差或系统误差的N维未知向量［4］。考虑一般的情形，可认为模型误差或观测值的系统误差的性态非常复杂，无法用少数参数表示，因此，给每个观测方程增加一个待定量，也就是所谓的非参数分量。这样再观测方程中既有参数分量又有非参数分量，因此，式（2）称为半参数模型［5］。

根据式（2）可写出误差方程为

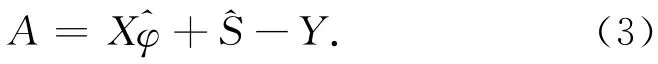
根据最小二乘原理

得到法方程

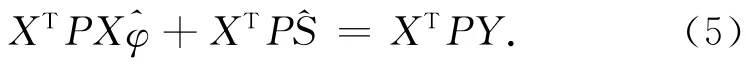
式中：P为对称正定方阵，是观测值Y的权，未知量为参数φ和非参数S，共有N个，而方程只有N－P个。所以从式（5）无法得到唯一解，因此，需要修改平差准则。一个合理的选择为

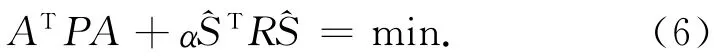
式中：R是一个适当的正定矩阵，称为正规化矩阵，二次型STRS反映对向量S的某种度量，α是一个给定的纯量因子，在极小化过程中对A和S起平衡作用，称为平滑因子。这时可把平差问题归结为一个条件极值问题。由拉格朗日乘数法［6］，构造函数

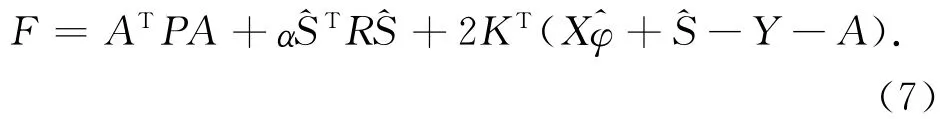
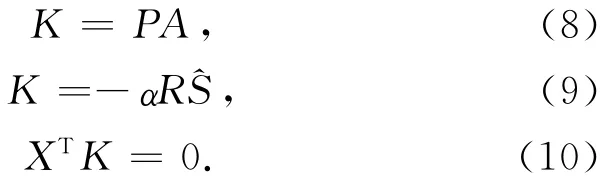
将式（8）代入式（10），考虑到式（3），得

令H＝XTPX，由于H可逆，所以有

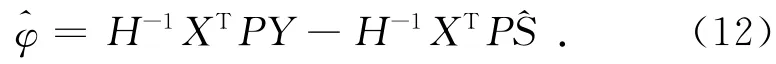
由式（3）左乘P，考虑到式（8）、式（9），得

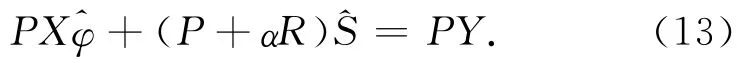
将式（12）代入式（13），经整理得到令M＝P＋αR－PXH－1XTP，则

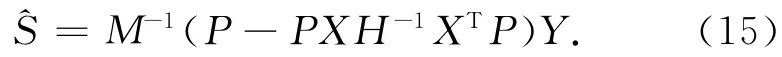
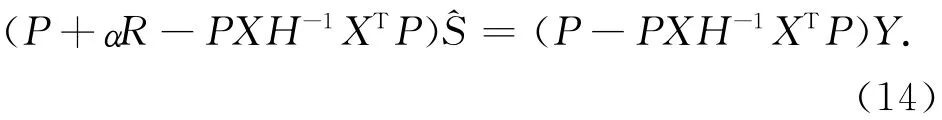
这样就可以通过式（15）、式（12）及式（3）计算非参数分量的估值S、参数分量的估值及观测值改正数A。通过分析得到的非参数分量，就可以重新认识所选的数学模型，从而实现对模型的精化。在上述分析中，平滑参数α、正规化矩阵R都是事先给定的量，R的选择与具体问题有关。

3 算例分析

数据来源：以某地东西向长约700m的短水准为例，见表1。

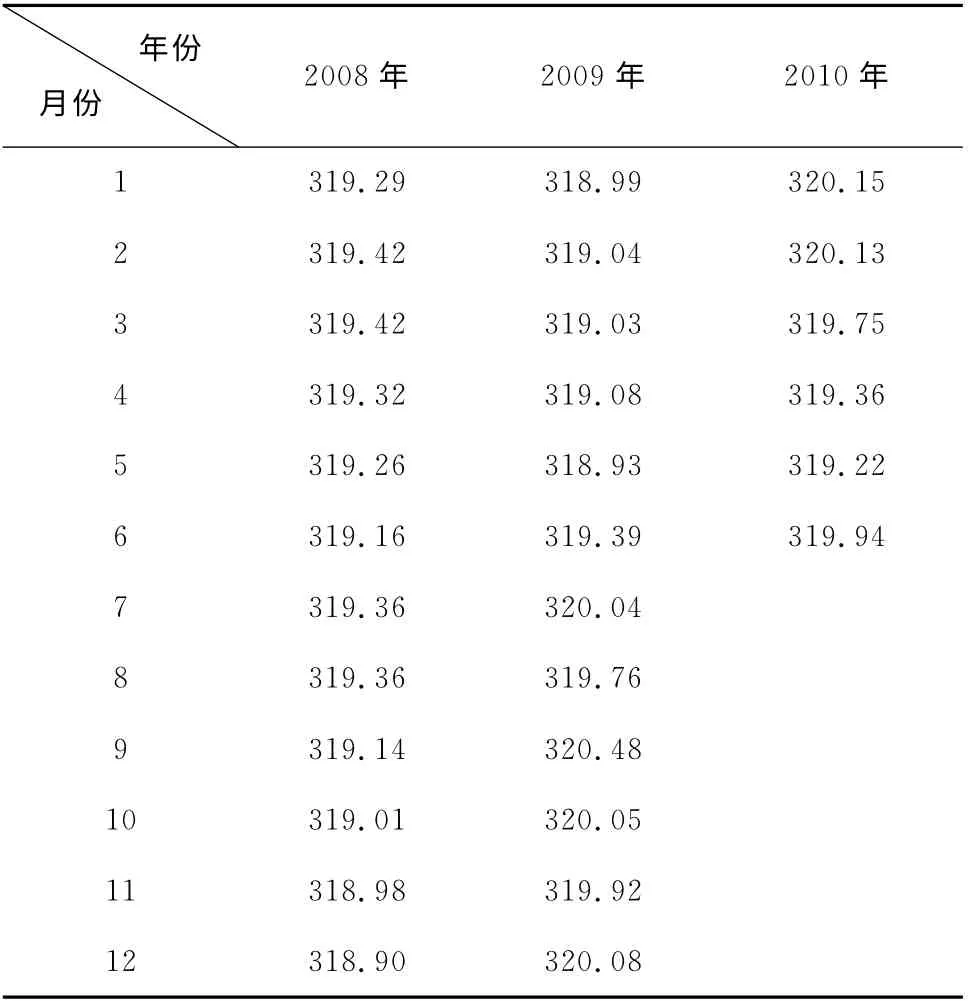
表1 数据来源

1）通过模型Y＝Xφ＋AT（AR模型），F检验求阶数可得p＝2。

2）通过AR（p）模型Y＝Xφ＋AT求解，编制程序将阶数p＝2代入计算得到结果如下：

XTX：（表示X的转置乘以X后再求逆，它是2行2列的矩阵）

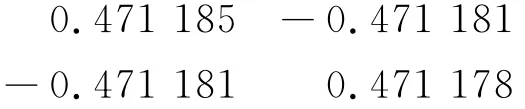
XTX×XT：（表示XTX乘以X的转置，它是2行28列的矩阵）

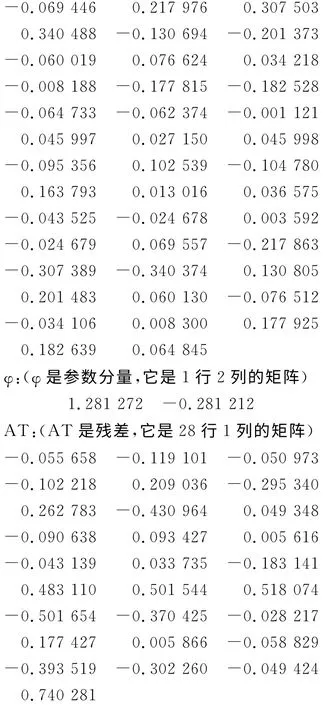
3）通过半参数模型AT＝Xφ＋S－Y求解，编制程序将阶数p＝2、系数A＝0.9（平滑系数）计算得到结果如下：

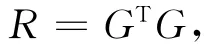
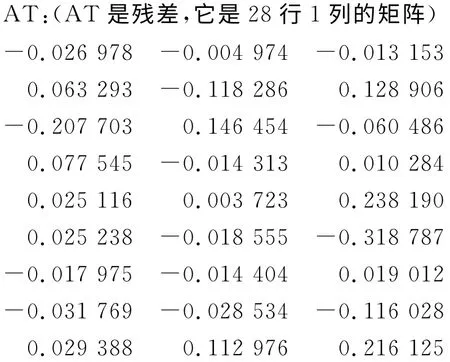
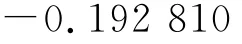
φ：（φ是参数分量，它是2行1列的矩阵）

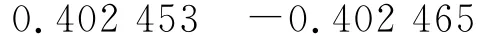
4）比较两模型的结果如下：

图1是分别用AR（p）模型和半参数模型求得的平差值图。x坐标表示第i个数据；y坐标表示各个平差值的大小。

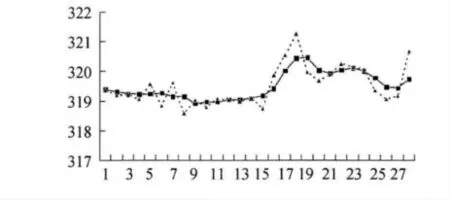
图1 AR（p）模型（虚线与▲）和半参数模型（实线与→）求得的平差值的比较图

从图中可以看出用AR（p）模型求得的平差值的变化较大而且快，曲线也不光滑；而用半参数模型求得的平差值的变化小，而且慢，曲线也非常光滑；由此可以看出当观测值中存在粗差或模型中存在模型误差时得出来的结果是不精确的或是错误的；而引入半参数后，就可以检查出一般模型不能检查出的粗差或模型误差，提高结果的精度。

4 结 论

当AR（p）模型存在模型误差或观测值中含有未参数化的系统误差时，常规的最小二乘平差很难发现和识别。使用附加系统参数的平差法，只能引入少量系统性参数，往往无法描述复杂多变的模型误差，若引入系统性参数太多，则可能引起过度参数化而导致法方程病态。从本文的算例可见，若对模型误差不加处理，将给参数估计值带来不利影响，甚至会导致错误的结论，引入半参数后，就可以检查出一般模型不能检查出的粗差或模型误差，提高结果的精度。另外，模型误差本身也是一种有用的信息，找到模型误差的规律不仅可以对选用的数学模型加以改进，而且还可以根据这种信息对其他相关问题进行研究。

［1］吴云，孙海燕.半参数估计的自然样条函数法［J］.武汉大学学报：信息科学版，2004，29（5）：398－401.

［2］胡宏昌.半参数模型的估计方法及其应用［D］.武汉：武汉大学，2004.

［3］孙孝前，尤进红.纵向数据半参数建模中的迭代加权偏样条最小二乘估计［J］.中国科学，2003，33（5）：470－480.

［4］米川，张永杰.半参数模型与最小二乘配置模型的比较［J］.测绘与空间地理信息，2010，33（5）：206－208.

［5］潘雄，刘立龙，陈刚，等.半参数平差模型估计量的精度评定［J］.测绘工程，2008，17（6）：13－15.

［6］王成勇.半参数回归模型研究综述［J］.数理统计与管理，2009，28（5）：845－357.