轴对称拉深成形法兰区起皱失稳变形能及临界压边力

秦泗吉 梁韶伟 张树栋

燕山大学先进锻压技术与科学教育部重点实验室，秦皇岛，066004

0 引言

拉深成形工艺广泛用于冲压生产，起皱和破裂是成形制件的两种主要失效形式。前者属于压缩失稳，后者属于拉伸失稳。一般来说，起皱失稳问题较破裂问题复杂得多。

目前有限元分析技术已被广泛用于板料成形过程的模拟，可以预测各种成形缺陷。而建立失稳判定条件以及判定失稳预测结果的准确性，则需要进行理论分析，并用实验进行验证。

塑性加工问题很复杂，一般很难采用纯理论的方法进行解析求解。以轴对称拉深成形为例，在法兰区建立起皱失稳条件，必须先给出应力、应变以及变形能的解析表达式，其中对法兰区应力的解析分析更是解决起皱失稳问题的关键，即便是在平面应力假设条件下，也很难直接给出应力的解析表达式，且无法得到应变的表达式。因此，目前常用的处理方法是:根据法兰变形区等效应变从法兰外缘到内缘是逐渐增大的这一规律，假设等效应变与瞬时径向坐标成简单的反比例关系［1-3］，求出应力的解析式，然后再计算变形能，进而求出起皱失稳临界压边力。

显然，在法兰区等效应变与位置关系成反比的假设条件与体积不变条件不一致，计算结果可能与实际相差较大。

本文以轴对称拉深成形为例，采用能量守恒原理，对法兰区起皱问题进行了分析。首先采用平面应变假设条件，对法兰区的应力分布进行了分析，根据应力分布特点，以数学方法进行了简化。然后根据径向应力的简化公式以及变形能随拉深位置的变化规律，采用分部积分法，得到了起皱失稳变形能的表达式，并给出了临界压边力的计算式。

1 能量法求解起皱失稳问题基本方程

板坯起皱失稳分析通常采用分叉理论［4-5］和能量守恒原理［6-7］。由于能量守恒原理更简明且更具普遍性，故得到了广泛应用。根据能量守恒原理，在起皱失稳瞬间，设由板坯周向伸长导致的周向应力释放的变形能为Uθ，板坯失稳起皱时弯曲所需的变形能为Uw，由于皱纹隆起压边力做功为 UQ，则有如下关系［6］:

在起皱失稳瞬间，周向应力σθ释放出的能量为［1］

式中，S'为失稳起皱后单波的周长变化量;σθ为在任意半径ρ处的周向应力;t为板厚;dρ为径向坐标位置增量;r0为凹模入口处的半径;Rw为法兰外缘半径;l为单个皱纹的波长;ds、dx分别为单波微弧段的弧长及其在x轴上的投影长度;y=y(x)为挠度方程。

一般情况下，将法兰变形区皱纹模型假设为

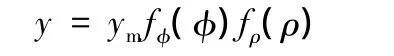
其中，ym为皱纹幅值;fρ(ρ)是与 ρ相关的函数;fφ(φ)是与φ相关的函数(φ为单波中任意弧段所对的圆心角);fρ(ρ)和 fφ(φ)是相互独立的量纲一函数。

由 x= ρφ，dx= ρdφ，得

通常取［1-3］

因而有

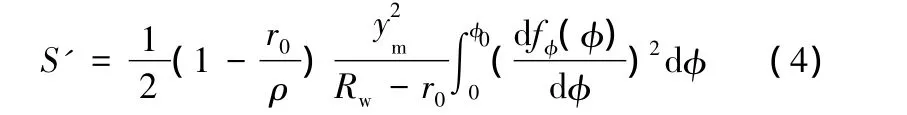
式中，φ0为单波所对的圆心角;r0为法兰内半径，即不考虑凹模圆角时的凹模口半径。

将式(4)代入式(2)，得

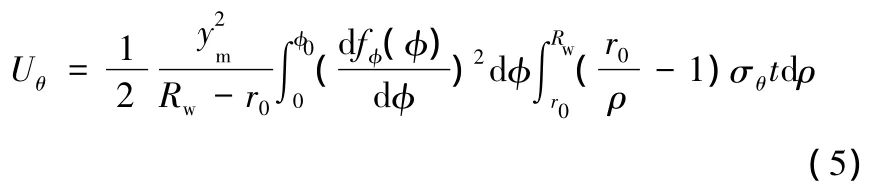
另一方面，法兰起皱后，波纹隆起为塑性弯曲。在起皱瞬间，假设波纹挠度不大，可认为是在加载条件下发生的，并仍然满足弹性弯曲时的小变形假设，分析计算中用塑性切线模量D替代弹性模量，波纹挠度与坐标ρ有关，因此有

而

因而

上式代入式(6)，且 dI=t3dρ/12，则有

设等效应力σ与等效应变ε符合幂指数的材料模型假设，则有

式中，B为板材的强度系数;n为硬化指数。

将式(8)、式(3)代入式(7)，得

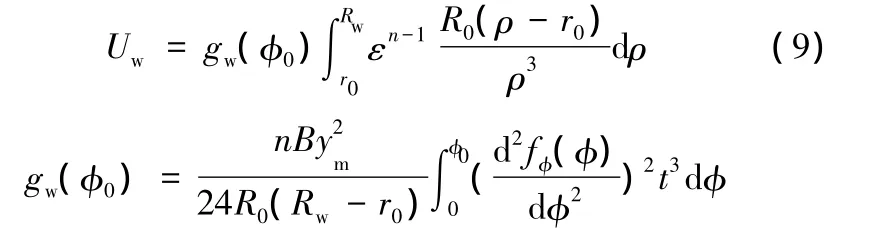
式中，R0为板坯初始半径。

式(5)、式(9)表明，起皱失稳变形能的计算需要首先已知应力应变分布规律。对轴对称拉深成形问题，在一定的假设条件下，可以求出应力、应变分布规律。但应力应变难以直接给出解析表达式，这使得后续工作无法进行。通常的处理方法是假设等效应变与位置关系成反比［1-3］，但这种假设显然与体积不变条件相悖。考虑在压边条件下，法兰区的板厚变化不大，在求解应力分布时，许多文献仍采用平面应变假设。以下在对法兰区应力进行求解分析的基础上，采用平面应变假设条件，进一步给出起皱失稳变形能、临界压边力等的简化计算方法。

2 平面应变假设条件下的应力分布

2.1 应力分析

对轴对称拉深成形问题，法兰区满足的平衡方程为

式中，σρ为法兰区径向应力。

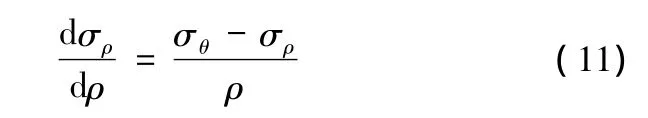
在平面应变假设条件下且不考虑摩擦等，根据式(11)及其他条件可求出法兰区的应力［8］。

若设半径为ρ处的变形质点的初始位置为ρ0，r为板厚方向性系数，则由等效应变的定义有

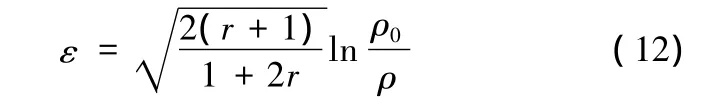
根据平面应变假设及等效应力的定义，有

根据平面应变假设条件、Mises屈服准则及幂指数的材料模型假设，得

因法兰外缘径向应力已知，则在法兰区任意位置ρ(ρ∈［r0，Rw］)处变形质点的径向应力为

式(16)中的x表示变形质点的相对位置。

将式(16)代入式(13)，并考虑等效应力等效应变关系、幂指数的材料模型假设，可求出周向应力。显然，周向应力也是包含积分项的函数式，它是质点坐标位置的函数，再将其代入式(5)，才能计算变形能Uθ，即便采用数值方法，计算过程也非常复杂。因此，将式(16)进行简化还是非常必要的。

2.2 应力表达式的简化

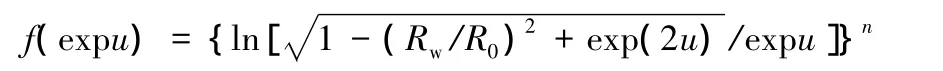
取 r0/R0=0.5，n=0.21，当 Rw/R0取不同值时，将函数f(expu)随u的变化规律表示在图1上。对于给定的 Rw/R0，在 u∈［ln(r0/R0)，ln(Rw/R0)］内f(expu)接近线性分布。表1给出了在Rw/R0和 r0/R0取一系列不同值时，函数f(expu)线性相关系数的平方值R2。结果显示R2均接近1。因而f(expu)在u的取值区间内线性相关密切，基本符合线性分布规律。容易验证，当n在0.2附近变化时，上述规律不变。

图1 函数f(expu)随u的变化规律

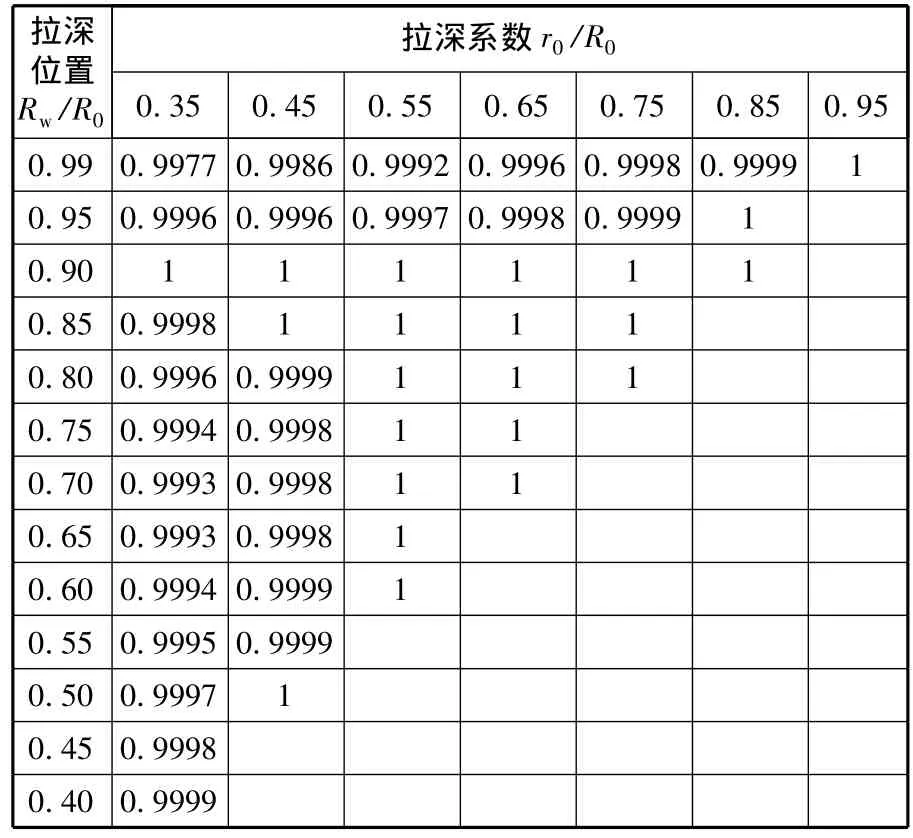
表1 函数f(expu)线性相关系数的平方值R2(n=0.21)

进行变量代换后，因积分函数近似为自变量u的线性函数，因而径向应力可以简化为自变量u的二次函数。参照文献［8］，以积分形式表示的应力表达式(16)，采用泰勒级数展开的方法，可按下式进行简化:

简化后的求解结果与原积分式求解结果非常接近。文献［8］给出的算例中，在n=0.19时，最大相对误差小于0.6%。

只有已知应力分布规律，才能计算起皱失稳变形能，而简明的应力表达式也为变形能的计算及进一步给出起皱失稳判据提供了便利。

3 起皱失稳变形能的计算

3.1 周向应力释放的能

分析式(5)，因σθ是ρ的函数，因而需要首先求出周向应力，才能确定周向应力释放的变形能。

根据平衡方程式(10)，式(2)可写为

由分部积分法，得

而S'可看为ρ的函数，因S'(r0)=0(法兰凹模入口处无皱纹高度为0，因而周向伸长也为0)，故可根据边界条件，得

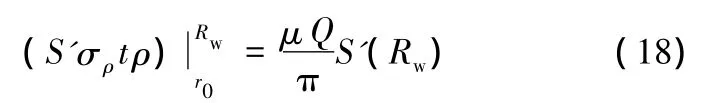
将ρ=Rw代入式(4)，得

且

因此

考察式(19)中的第一项，令ρ/R0=expu，由

式(17)可知，径向应力可近似表示为u的线性函数，因此有

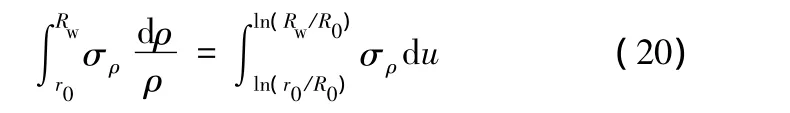
当μ=0时，若设σρ=ka+kbu+kcu2，则式(20)是可积函数，即

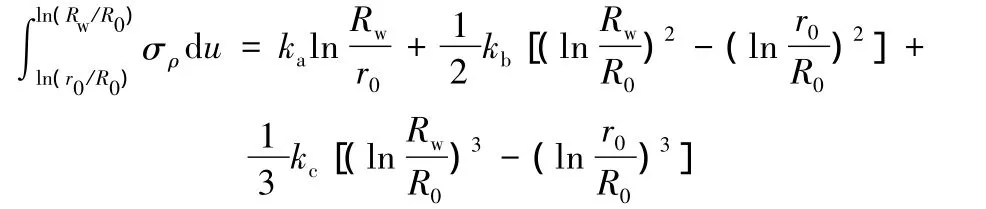
取μ =0，Rw/R0=0.85，r0/R0=0.5，n=0.21，采用式(19)(用数值方法)计算得到的结果和采用简化式计算得到的结果非常接近，其相对误差小于0.8%。可以验证，当计算参数在可行范围内变化时，误差也很小。

若进一步设

则有

3.2 弯曲变形能

根据面积不变假设，将等效应变的表达式式(12)代入式(9)，得

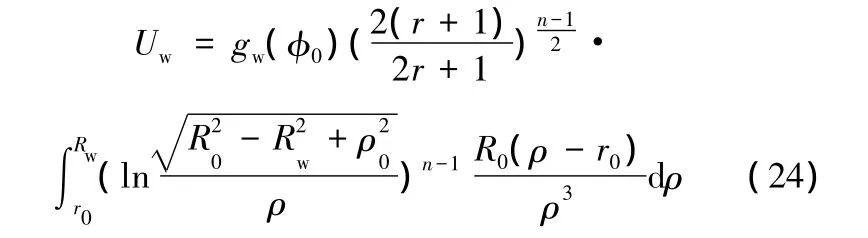
4 临界压边力及理想压边力行程曲线

4.1 起皱失稳临界压边力

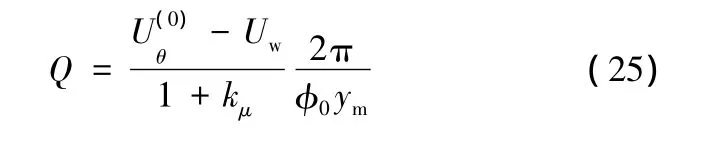
在不考虑成形速度、温度等成形条件对起皱影响的前提下，式(25)给出了压边力与材料性能参数、板坯几何参数、拉深位置参数以及皱纹模型参数之间的关系。当成形条件、材料性能参数、板坯几何参数以及拉深位置参数一定时，压边力仅与皱纹模型几何参数有关。

当其他参数一定时，压边力是皱纹模型参数的函数，在临界起皱条件下，一般允许的皱纹幅值有一定的设定值，此时，压边力仅是皱纹数量N或单个皱纹的圆心角φ0的函数。由式(25)，令压边力对φ0的一阶偏导数为0，可得到临界压边力下的φ0，将φ0再代入式(25)，可以求出临界压边力。可以验证式(25)给出的Q是φ0的单凸函数，即临界压边力是所有可能的压边力取值中的最大值。

图2所示是当量压边力Q/ym(压边力与皱纹幅值之比)随皱纹数量的变化曲线。可以看出，当皱纹数量为某一数值时，压边力达到最大值，这就是临界压边力。在实际拉深过程中，当其他参数不变时，临界压边力是拉深位置的函数，即压边力随行程是变化的，这就是理想压边力行程曲线。显然，在拉深开始和拉深结束时，临界压边力都为0，而在中间的某个拉深位置，临界压边力达到最大值。在拉深过程中，若保证施加的工艺压边力都不小于临界压边力，则能确保拉深过程不产生起皱失稳。

图2 Q/ym与皱纹数量的关系曲线(μ =0.08，n=0.18)

4.2 理想压边力行程曲线

图3所示是临界当量压边力Q/ym与拉深位置Rw/R0(法兰外缘的相对位置)的关系曲线，由于拉深位置与拉深行程有一一对应关系，因此该曲线是理想压边力行程曲线的另一种表达形式。

5 结论

(1)在平面应变假设条件下，分析了轴对称拉深成形起皱失稳条件下的变形能，导出了计算式。

图3 Q/ym与拉深位置的关系曲线(μ=0，n=0.18)

(2)用分部积分法、泰勒级数等数学方法简化了变形能的计算式。新的计算式更简明实用，与原积分形式表示的计算式非常接近。给出的算例表明，相对误差小于0.8%。

(3)分析了起皱失稳临界压边力和理想压边力行程曲线的含义，并给出了算例。

［1］梁炳文，胡世光.板料成形塑性理论［M］.北京:机械工业出版社，1987.

［2］赵军，张双杰，曹宏强，等.拉深过程智能化控制中的法兰起皱临界条件［J］.燕山大学学报，1998，22(3):197-201.Zhao Jun，Zhang Shuangjie，Cao Hongqiang，et al.Critical Flange Wrinkle Condition in Intelligent Control of Deep Drawing Process［J］.Journal of Yanshan University，1998，22(3):197-201.

［3］罗亚军.板材拉深成形变压边力理论和数值模拟［D］.上海:上海交通大学，2003.

［4］Hill R.A General Theory of Uniqueness and Stability in Elastic/Plastic Solids［J］.Journal of the Mechanics and Physics of Solids，1958，6:236-249.

［5］Hutchinson J W.Plastic Buckling［J］.Advances in Applied Mechanics，1974，14:67-144.

［6］Senior B W.Flange Wrinkling in Deep－drawing Operations［J］.Journal of the Mechanics and Physics of Solids，1956，48:235-246.

［7］Yu T X，Johnson W.The Buckling of Annular Plates in Relation to Deep Drawing Process［J］.International Journal of Mechanical Sciences，1982，24(3):175-188.

［8］秦泗吉.轴对称拉深成形凸缘变形区应力的解析求解［J］.机械工程学报，2011，47(24):20-25.Qin Siji.Analytical Solution of Stress in Flange Deformation in Axisymmetrical Deep Drawing Process［J］.Journal of Mechanical Engineering，2011，47(4):21-25.