基于分数次幂多项式的NURBS曲线快速插补方法研究
朱 昊 刘京南 杨安康 汪木兰
1.东南大学,南京,210096
2.南京工程学院先进数控技术江苏省重点实验室,南京,211167
0 引言
非均匀有理 B样条(non-uniform rational B-spline,NURBS)是国际标准化组织在产品模型数据交换标准(standard for exchange of product model data,STEP)中规定描述自由曲线曲面的唯一数学模型。是否具有NURBS曲线插补功能是目前衡量一个数控系统技术水平的重要指标之一。近年来,关于NURBS插补的一个热点问题是如何将进给速度的控制融合到插补计算之中[1]。传统的速度控制方法有很多种,基于速度时间曲线的描述,常见模型类型包括直线型、指数型以及S型[2]。直线型速度控制方法简单、计算量小。相对于直线型控制方法,指数型速度控制方法具有平滑性好、运动精度较高的优点。但上述两种方法都存在加速度不连续、机床受冲击、加工质量不高的缺点。潘海鸿等[3]讨论了S型速度控制策略,这种控制策略实现了加速度的平滑过渡,但存在加加速度不连续的问题。赵国勇等[4]用分段三次多项式描述速度变化,设计了速度控制策略,该算法实现了加加速度时间曲线的连续性,但加加速度变化较缓慢,使得速度上升到最大值所需要的时间较长,影响了插补的快速性。
本文在考虑加加速度连续性、平滑性及其最大值限制的基础上,提出一种基于分数次幂多项式描述的速度控制策略,使得加加速度能快速增大至最大值,且过渡连续、平滑。
1 NURBS曲线直接插补方法
NURBS曲线直接插补是指将整条NURBS细分为若干插补周期,在每个插补周期内控制刀具在三个坐标上运动,从而直接逼近NURBS曲线。目前一般按照时间进行分割,在确定不同位置刀具速度的基础上,首先根据加工路径曲率变化确定各插补点的速率vi,然后按照步进时间不变的原则求取插补步长ΔS。对于以参数ui表示的NURBS曲线P(u),可以根据步长ΔS确定下一点的参数值ui+1。通过ui+1可最终求取此点的坐标X、Y、Z 及其偏移量 ΔX、ΔY、ΔZ。在上述过程中,由于NURBS曲线的反函数难以计算,对于参数ui+1的求取一般采用Taylor展开近似算法来获取步长和参数的关系。对于NURBS曲线P(u),通过Taylor展开可以递推得到下一个参数的近似值。常用的二阶Taylor展开式如下[5]:

式中,T 为插补周期;v 为进给速度;X'、X″、Y'、Y″分别为X(u)和Y(u)的一阶、二阶导数。
根据式(1)通过De Boor递推公式即可根据参数ui+1最终求取此点的坐标X、Y、Z。
2 基于分数次幂多项式的速度控制
2.1 加加速阶段速度分析
当加工路径曲率发生变化时,机床插补的速度必须发生变化,否则将会带来过大的轮廓误差。文献[3]中讨论的速度控制模型将加速或减速过程分为三段,因此完整的加速 -匀速 -减速过程被分为七段。这是目前应用最为广泛的速度控制策略,其中加加速段模型为

式中,jmax为最大加加速度;vs为初始速度;t为时间。
文献[4]提出的速度模型能实现加加速度的连续,其中加加速段模型为
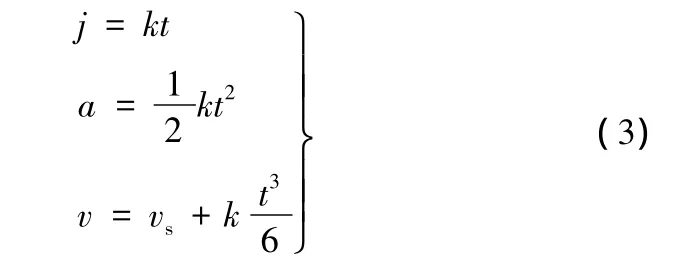
其中,系数k由机床自身特性决定。
由式(2)可以看出,加加速度为恒定值jmax,当速度模型由加加速过渡到匀加速时,加加速度将发生阶跃跳变,这种阶跃跳变将导致机床受到柔性冲击而影响加工精度。式(3)中加加速度呈线性变化,其变化率由系数k决定。系数k的取值取决于机床本身结构,对于不同结构的机床,系数k也不同。目前对系数k的特性及变化规律进行深入讨论的文献很少,还没有统一的结论。为使得加加速度更快地达到jmax且保持连续,本文提出基于分数幂多项式的速度控制策略,其中加加速度阶段模型如下:

式中,js为初始加加速度;as为初始加速度。
2.2 基于分数次幂多项式的速度控制模型
传统的七段法将加速过程分为三段:加加速过程、匀加速过程、减加速过程。在这3个过程中,加加速度分别为jmax、0、-jmax。减速过程与加速过程类似。本算法在七段法基础上,将加速和减速过程均进一步细分为七段。加速阶段的具体动力学模型如下:

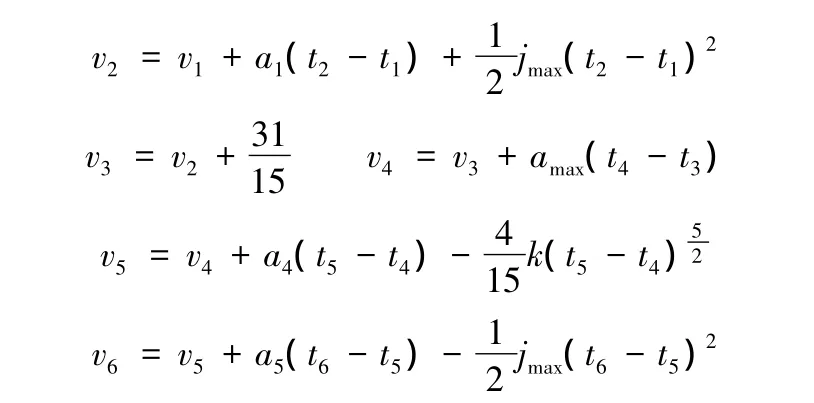
减速部分与之类似。这里按照一般情况,设加加速度和加速度的初始值均为0,速度初始值为vs。
3 相关约束条件
3.1 曲率半径的计算
曲率半径描述了曲线的弯曲程度。对于一条NURBS曲线P(u),在ui处的曲率半径Ri为

式中,P'(u)、P″(u)为 P(u)的一阶、二阶导数。
由NURBS曲线齐次坐标表示法可得

式中,Pi为 NURBS曲线控制点;Ni,k(u)为 B 样条基函数。
因此,可得

同理,可求得二阶导数P″(u),并将其代入式(8)即可求出该点处曲率半径。
3.2 基于弓高误差的速度约束
设相邻两个点ui和ui+1之间的弓高误差为ε,ui点处加工半径为ri,则根据弓高误差的定义可得

由Li=viT可得

为保证加工精度,在弓高误差的约束下,在ui处的速度vc应该满足如下关系:
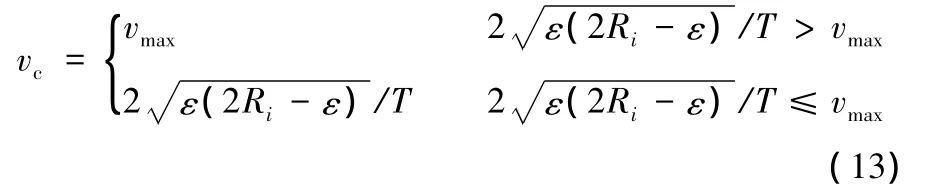
3.3 基于加加速度最大值的速度约束
在插补过程中,除加加速度不连续会对机床产生柔性冲击外,加加速度绝对值过大也同样会对机床产生影响。文献[6]讨论了加加速度与进给速度的关系,并推导了相应公式。对于NURBS曲线P(u),加加速度j、加速度a以及速度v之间的关系如图1所示。

图1 单步插补中加加速度、加速度和速度的关系


由加加速度定义可得
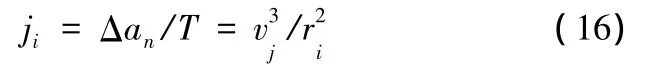
因此

4 基于曲率变化的前瞻算法
4.1 前瞻算法目标
当实际加工路径曲率以及长度发生变化时,第2节所述动力学模型将有所变化。当曲率变化相对剧烈,加工路径相对较短时,上述模型中可能没有匀加速阶段、匀速阶段以及匀减速阶段,甚至速度不能达到机床允许的最大速度vmax。前瞻算法的主要功能在于判断加速、减速阶段时间以及求取插补过程的减速点,并理论减速位移Sd相比较,从而确定上述模型的具体结构并修正实际进给速度。
4.2 加减速阶段分析
当加工路径曲率l发生变化时,加工速度随之变化,当加工路径为直线时,l=0,加工速度最大。因此可以根据加工路径的曲率求得加工路径中的速度极大区域。具体判断法则如下:
对于NURBS曲线P(u),设其参数ui处的曲率为li,则根据式(8)的倒数可以求得曲线上各点曲率值的集合{l0,l1,…,ln}。
(1)当其中某一个元素li的值为0时,则此元素li所对应点同时为加速过程的结束点和减速过程的起始点。
(2)当其中连续多个元素 li-t,li-t+1,…,li的值为0时,则此组中最左边一个元素li-t所对应点为加速过程的结束点,此组中最右边一个元素li所对应点为减速过程的起始点。
(3)设Δli=li-li-1为相邻两个点的曲率之差,则对于连续 3 个点 P(ui-1)、P(ui)、P(ui+1),存在 Δli、Δli+1。当Δli< 0且Δli+1> 0时,P(ui)同时为加速阶段结束点和减速过程的起始点。
(4)当Δli>0且Δli+1<0时,P(ui)同时为减速过程的结束点和加速过程的起始点。
4.3 减速点预测
设插补运动位移为S,则有

现将式(18)代入式(8)可以求出理论减速位移Sd。文献[7]给出了一种基于Sinpson求积法的NURBS总弧长St的计算公式。文献[8]给出了一种计算已走过弧长Sa的计算公式。则ΔS(ΔS=St-Sa)表示该段曲线实际剩余位移。根据上述参数,可得减速点判断法则如下。
对于NURBS曲线P(u),令各点处剩余位移为{St,ΔS1,…,ΔSi,…,ΔSn-1,0},则有:① 其中若存在某个元素ΔSi满足ΔSi=Sd,则P(ui)为实际减速点;②其中若存在连续两个元素 ΔSi,ΔSi+1满足ΔSi>Sd且ΔSi+1<Sd,则P(ui)为实际减速点。
5 仿真分析
由式(5)~式(7)可得在加速-匀速-减速阶段分数幂多项式速度控制策略(此处称为F算法)的加加速度时间曲线、加速度时间曲线和速度时间曲线。为验证其合理性,现与文献[3]中的七段法速度控制策略(此处称为S算法)和文献[4]中的三次多项式速度控制策略(此处称为T算法)作对比。考虑到比较条件的一致性,这里取 k=1,jmax=1mm/s3,amax=2mm/s2,vmax=8mm/s,vs=0。对比结果如图2所示。
从图2中可以看出,S算法加速度和速度变化较快,但加加速度出现了阶跃跳变。T算法和F算法实现了加加速度的连续,但F算法加速度和速度变化更加快速。可见本文提出的F算法可以在保证加加速度连续的条件下使得速度更快达到最大值。
为验证上述算法的正确性,本文在MATLAB中分别对二维和三维NURBS曲线进行了仿真,对加加速度连续的T算法和F算法进行了对比。二维NURBS插补路径如图3a所示,其控制点为(4,4,0)、(0,2,0)、(0,8,0)、(4,4,0)、(8,0,0)、(8,6,0)、(4,4,0)。权重向量为 w=(1,0.5,0.9,1,0.9,0.5,1)。节点向量为 U=(0,0,0,1/4,1/2,1/2,3/4,1,1,1)。三维 NURBS 插补路径如图3b 所示,其控制点为(3,1,0)、(2,3,2)、(4,2,1)、(5,4,3)、(6,2,1)、(8,3,2)、(7,1,0)。权重向量为 w=(1,0.5,0.9,1,0.9,0.5,1)。节点向量为 U=(0,0,0,1/5,2/5,3/5,4/5,1,1,1)。
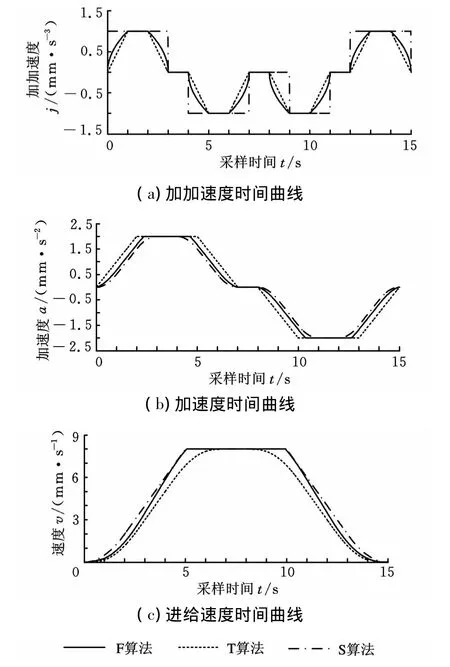
图2 F算法、T算法、S算法速度控制策略比较

图3 二维和三维NURBS曲线插补路径
加工参数如下:插补周期T=1ms,最大进给速度 vmax=100mm/s,最 大 加 速 度 amax=250mm/s2,最大弓高误差 ε=1μm。二维 NURBS曲线初始进给速度vs=70mm/s,插补速度时间曲线如图4a所示。三维NURBS曲线初始进给速度vs=0,插补速度时间曲线如图4b所示。从图4a和图4b中可以看出,F算法中进给速度可以更快地到达速度最大值。在实际加速位移较短,进给速度无法达到vmax时(如二维NURBS曲线的控制点(4,4,0)与(0,2,0)之间和三维 NURBS 曲线的控制点(2,3,2)与(4,2,1)之间),F 算法中进给速度可以达到相对较高的值。
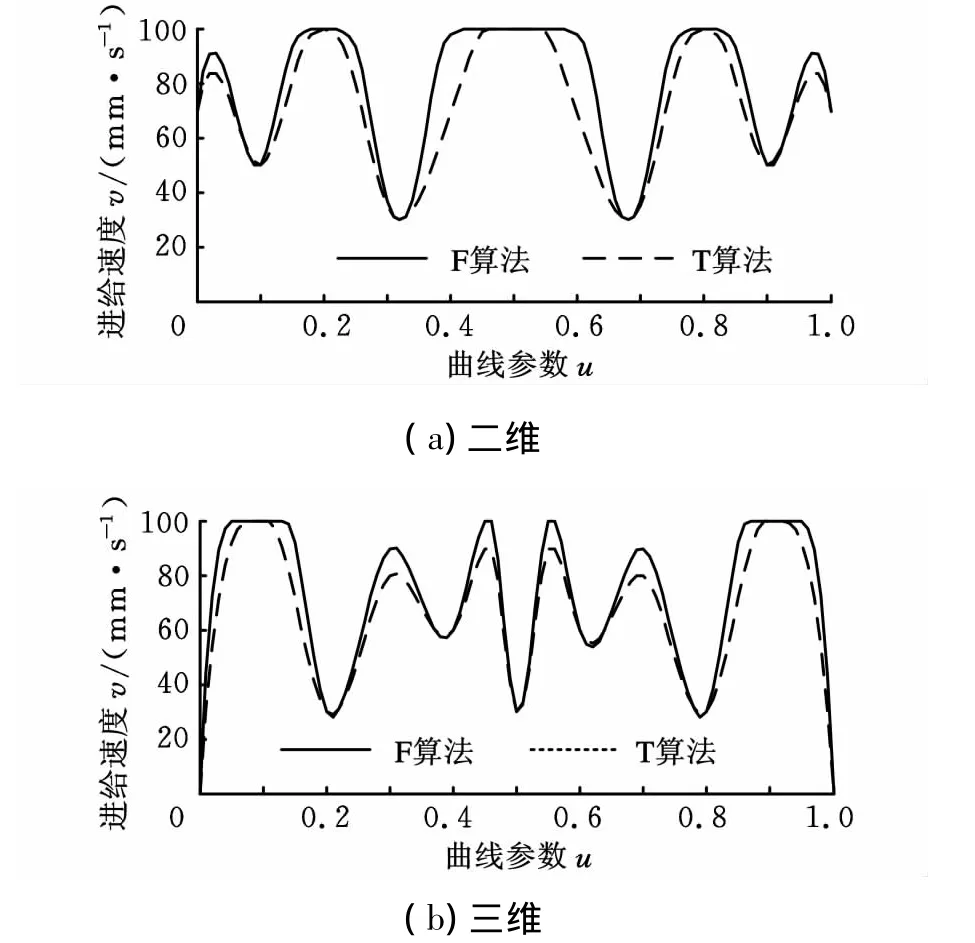
图4 二维和三维NURBS曲线F算法、T算法速度响应
6 结束语
本文在分析现有算法的基础上有针对性地提出了基于分数次幂多项式的速度规划方法,分析了基于加加速度控制约束的约束条件,根据曲率的变化讨论了加减速阶段及减速点的计算方法并给出了判断法则。分析结果表明,本算法可以在保证加加速度连续的前提下有效提高加工速度,满足了NURBS曲线高速高精度的插补要求,将本算法应用于实际计算机数控系统有切实的实用价值和可行性。考虑到篇幅限制,本文并未讨论如何将上述算法嵌入到真正数控机床中予以实现。
[1]Kong T,Narayanawami R A.Parametric Interpolator with Confined Chord Errors,Acceleration and Deceleration for Machining[J].Computer- aided Design,2003,35(13):1249-1259.
[2]胡建华,廖文和,周儒荣.CNC系统中几种升降速控制曲线的研究和比较[J].南京航空航天大学学报,1999,31(6):706-711.Hu Jianhua,Liao Wenhe,Zhou Rurong.Research and Comparison for Several Curves of Acceleration and Deceleration in CNC Systems[J].Journal of Nanjing University of Aeronautics & Astronautics,1999,31(6):706-711.
[3]潘海鸿,杨微,陈琳,等.全程S曲线加减速控制的自适应分段NURBS曲线插补算法[J].中国机械工程,2010,21(2):190-195.Pan Haihong,Yang Wei,Chen Lin,et al.Adaptive Piecewise NURBS Curve Interpolator Algorithm for Entireness Process S-curve ACC/DEC Control[J].China Mechanical Engineering,2010,21(2):190-195.
[4]赵国勇,徐志祥,赵福令.高速高精度数控加工中NURBS曲线插补的研究[J].中国机械工程,2006,17(3):291-294.Zhao Guoyong,Xu Zhixiang,Zhao Fuling.Study on NURBS Curve Interpolator in the High Speed and High Accuracy CNC Machining[J].China Mechanical Engineering,2006,17(3):291-294.
[5]Yang D C H,Kong T.Parametric Interpolator Versus Linear Interpolator for Precision Surface Machining[J].Computer-aided Design,1994,26(3):225-234.
[6]Lai J Y,Lin K Y,Tseng S J,et al.On the Development of a Parametric Interpolator with Confined Chord Error,Federate,Acceleration and Jerk[J].Advanced Manufacture Technology,2008,37:104-121.
[7]Le W T,Sung I M P,Huang J J.Fast Real-time NURBS Interpolation for CNC Machine Tools[J].Machine Tools & Manufacture,2007,47:1030-1541.
[8]Altintas Y.Metal Cutting Mechanics,Machine Tool Vibrations,and CNC Design[M].Cambridge:Cambridge University Press,2000.

