机械行波传动器理论建模与实验研究
宋瑞银 蔡炳清,2 张向阳,2 周敏珑,2
1.浙江大学宁波理工学院,宁波,315100 2.太原科技大学,太原,030024
0 引言
行波是一种质点上下振动同时波形又向固定方向移动的一种波形,其驱动机理在很多文献中已有阐述,其应用主要集中于超声波电机中[1-3]。本文提出一种全新原理的传动机构,它利用机械驱动激波发生器产生行波,利用行波驱动从动机构运动的原理实现传动,其结构相对简单,可靠性强,可用于大传动比、微机电系统等一些特殊要求的场合。本文建立了该行波传动器的理论模型,并进行了初步实验分析。
1 行波传动器的结构原理

图1 行波传动机构结构原理图
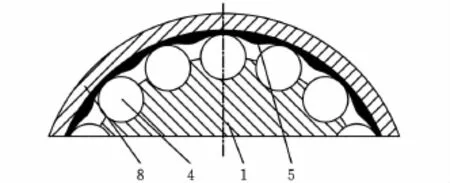
图2 激波发生器断面图
机械行波传动器的结构原理如图1所示,主要包含输入轴、输出轴、激波发生器等,核心在于由弹性应变层5和由周期性间隔的滚柱4构成的激波发生器。激波发生器断面如图2所示,为圆环状,也可设计为圆锥状或圆柱状。应变层与输入轴滚柱的接触面光滑,而输出轴内圈涂有一层摩擦材料,以保证弹性应变层与输出轴接触面间有较大的摩擦因数。输入轴转动时,将带动滚柱转动,圆环状的弹性应变层在受到滚柱径向挤压后,弹性体将向滚柱两侧变形(图3a),当滚柱离开弹性体接触点后,弹性体将回弹(图3b),从而使弹性体内部质点沿着环面形成拉伸-压缩-拉伸的周期性往复运动并使环面质点沿径向振动。同时考虑沿着周向连续的转动,振动形成行波,则在弹性体内的质点将形成椭圆状的质点运动,进而驱动输出轴运动。

图3 激波发生器行波形成机理
将传动机构弹性体的中性层沿圆周展开,形状如图4所示,它反映了弹性应变层产生行波的形状和弹性应变层质点的运动轨迹,和输出轴接触的一系列质点运动轨迹呈椭圆状[4-7]。图4中,假设行波右行,质点的椭圆运动轨迹为逆时针。弹性应变层质点在行波驱动下会产生椭圆振动,设图中质点处于行波波峰点即椭圆振动最高点时,其波动速度水平向左,在一定的预紧力条件下,弹性应变层质点的水平运动将对输出轴产生摩擦驱动力,由此带动输出轴向左运动,反之亦然。

图4 弹性体表面质点的椭圆运动轨迹
2 行波传动机构的理论建模
如图4所示,将弹性体沿圆周方向展开后,接触模型就变为平面二维问题。P0、P分别为弯曲变形前后的点,弯曲变形后的弯曲角为θ,则从P0到P沿厚度方向的横向振动位移为u。设弹性体厚度为h,输入轴滚柱数目为 N,输入轴转速为n(r/min),在弹性体中性层上建立坐标系xz,则根据弹性体中性面的弯曲行波理论[5,8]可得P0到P的纵向振动位移w(x,t),其数学模型为

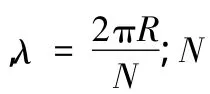
这里不考虑弹性层和输出轴转子间的滑动,则输出轴转子速度等于弯曲波波峰处质点的振动速度。对式(1)求偏导,得到弹性体质点纵向振动速度为
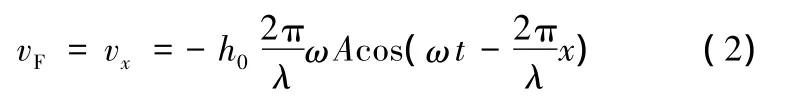
其中,h0=h/2,表示弹性体表面处的质点位置为椭圆运动轨迹最高点。式(2)中负号表示弹性层表面质点运动到波峰处时的运动方向正好与行波方向相反。



图5 转子的速度波形图
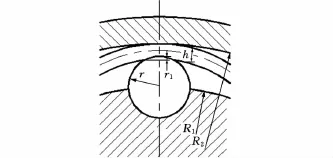
图6 传动器部分零件尺寸
由图3可知,滚子对弹性体的最大挤压变形量即为弹性体的振幅,即r1=A。将输入轴的转速换为弹性体中性层的线速度vi,有

设输入轴和输出轴之间的预紧力为F,则单个滚子所受的法向预紧力为Fc=F/N。
弹性体受到刚体滚子挤压的变形量为r1(r1=A),设弹性体的弹性模量为E,圆柱滚子长度为B(也为弹性层有效接触宽度),则挤压接触面积为

将式(5)代入应力计算公式,并考虑到挤压变形量较小,加以化简后可得到接触层受的应力为

在一个波长周期内,接触层的应变可近似表示为[9-10]

式中,2L为输入输出轴在一个波长内的接触长度。
取应变在正半周期的平均值,得到在有效推动时的应变平均值为
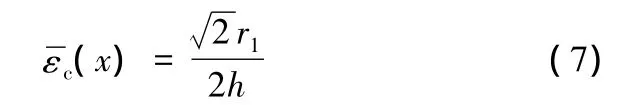
由应力应变的关系式σc=Eεc,并考虑到振动幅值r1值相对r较小,将该式(7)化简(求解时去掉四次方的未知量),得到挤压变形量和法向预紧力间的关系为

将式(8)代入总传动比公式,化简得到:

可见,传动器总传动比与弹性层厚度、弹性体材料、预紧力、输入轴(输出轴)半径、滚柱数目、滚子半径、振幅等均有关系。
3 测试模型及平台搭建
在前述的机械行波传动理论模型基础上设计了一套机械行波传动测试装置,如图7所示。测试装置中,由驱动电机驱动输入轴转动,转速由转速传感器测量,输入轴转动带动机械激波发生器转动,进而使弹性应变层产生机械行波。为便于观察和测试,这里将原设计的输出轴用直线移动尺代替。弹性层产生机械行波后,直线移动尺将产生位移,位移通过位移传感器测量得到。预紧力调节器为丝杆螺母副,通过旋转螺母可调节直线移动尺和弹性层间的预紧力。

图7 机械行波传动测试装置
4 实验测试与分析
由理论模型可知,传动器总传动比与弹性层厚度、弹性体材料、预紧力、输入轴及输出轴半径、滚柱数目、滚子半径、振幅等均有关系。由于参数较多,实验中,把弹性体材料、输入轴及输出轴半径、滚柱数目、滚子半径设为不变量,把弹性层厚度、预紧力作为可调变量进行实验测试。为减小外界摩擦对位移的影响,这里采用了铝质滑台,与PP材料做的直线移动尺直接接触。传动测试装置中,输入轴半径为20mm,滚珠数量为11个,均布在弹性层内圈,滚子半径为1.8mm,滚子宽度为9mm,输入轴转速为136r/min,弹性应变层中性层的直径为48.16mm。
4.1 弹性层厚度对传动比影响测试
弹性层是机械行波产生的核心部件,这里加工了厚度分别为3mm、5mm、7mm和9mm的几种弹性层。通过调节精密滚珠丝杆上的螺母来改变滑块和弹性层间的预紧力。在实际测试中,调节丝杆高度,使弹性层与直线位移尺的接触变形量在0.5mm,起始位置设定为零,每间隔30s记录一次直线位移尺移动的距离s,测试中循环4次,取平均值,4种输出位移曲线如图8所示。由图8可以看出,在弹性层厚度和预紧力确定后,直线移动尺移动速度基本保持恒定,减速比在401.7左右,这表明机械行波驱动器具有较大的传动比。其次,从弹性层厚度对传动比的影响来看,随着弹性层厚度的增加,在210s内直线位移s从189mm降至150mm,这表明弹性层厚度对传动比有一定的影响,但影响效果不明显。

图8 不同弹性层厚度时铝块的位移量
4.2 预紧力对传动比的影响测试
通过调节丝杆上的螺母来调节直线位移尺和弹性层间的预紧力,设置每次的调节距离为0.5mm,选择了3mm和5mm两种厚度的弹性层作为实验,得到传动比i和弹性层变形量Δ的变化曲线,如图9所示。

图9 弹性层变形量与传动比的关系
从图9可以看出,随着预紧力的增加(即弹性层变形量的增大),机构传动比值呈下降趋势;同时,随着弹性层厚度的增加,传动比呈下降趋势,这与理论模型相符合。
5 结论
本文提出了一种新型的行波传动机构,并在机构设计的基础上进行了理论建模。借鉴国内外现有超声波电机的研究理论和基础,初步建立了总传动比、输出力矩、输出功率等数学模型。在初步设计的基础上设计并加工了测试用行波传动机构。通过对传动机构的测试,得到了行波传动机构具有如下特点:可得到较大的传动比,且结构相对简单。实验结果也初步证明了理论模型的正确性。
传动器总传动比与弹性层、预紧力、输入轴(输出轴)半径、滚柱数目与半径等多个参数有关,尤其是弹性层及摩擦层的材料等参数对传动机构的机械性能影响较大。弹性层及摩擦层间存在较大功率损耗,这也导致传动效率较低。为了得到总体的传动机理等理论模型,主要从宏观方面进行了假设和近似取值,更精确的理论模型有待从行波传动的摩擦传动的微观摩擦机理进行进一步的研究。
[1]朱美玲,金龙,赵淳生.行波超声马达传动机理的研究(一)——运动传递机理及定子中存在弯曲行波的条件[J].振动、测试与诊断,1996,16(4):7-14.Zhu Meiling,Jin Long,Zhao Chunsheng.Research on Transmission Mechanism of Piezoelectric Traveling Wave Ultrasonic Motors Part I:Mechanism of Motion Transmission and Conditions for the Existence of a Bending Traveling Wave in the Stator[J].Journal of Vibration,Measurement& Diagnosis,1996,16(4):7-14.
[2]Ueha S,Tomikawa Y.Ultrasonic Motors Theory and Applications[M].Oxford:Oxford Science Publication,1993.
[3]LeMoal P,Cudsin P.Optimization of Traveling Wave Ultrasonic Motors Using a Three-dimension Analysis of the Contact Mechanism at the Stator Rotor Interface[J].Eur.J.Mech.A/solids,1999,18:1061-1084.
[4]石斌.环形行波型超声马达的研究[D].南京:东南大学,2001.
[5]刘锦波.超声波电机的数学模型及其驱动系统的研究[D].杭州:浙江大学,1998.
[6]胡敏强,金龙,顾菊平.超声波电机原理与设计[M].北京:科学出版社,2005.
[7]Hagood N W,Mcfarland A J.Modeling of a Piezoelectric Rotary Ultrasonic Motor[J].IEEE LJFFC,1995,42(2):210-224.
[8]刘锦波,陈永校.超声波电机定转子接触的摩擦传动模型及实验研究[J].中国电机工程学报,2000,20(4):59-63.Liu Jinbo,Chen Yongxiao.Investigation on Contact Model of Ultrasonic Motor and Its Experiments[J].Proceedings of the CSEE,2000,20(4):59-63.
[9]Maneo T,Tsukimoto T,Miyake A.Finite Element A-nalysis of the Motor/stator Contact in a Ring-type Ultrasonic Motor[J].IEEE Trans.on UFFC,1992,39(6):668-674.
[10]贺红林,曾劲松,龙玉繁,等.行波超声电机的运转特性及其电学建模研究[J].中国机械工程,2011,22(14):1639-1644.He Honglin,Zeng Jinsong,Long Yufan,et al.Modeling of Operating Characteristics of Ultrasonic Motor Using Equivalent Circuit[J].China Mechanical Engineering,2011,22(14):1639-1644.

